Skip to main content
SpringerLink
Log in

Optimization of the Spectral Processing of the Signal of a Precision Distance Sensor Based on a Frequency Rangefinder

  • Linear and Angular Measurements
  • Published:
Measurement Techniques Aims and scope

Abstract

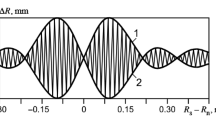
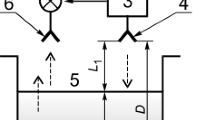
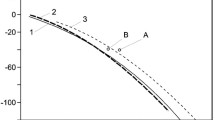
We have derived an expression for the error of method in difference frequency measurements for a distance sensor based on a frequency range finder. We employed weighted average estimation for a broad class of weighting functions and examined the structure of the error. Quantitative estimates have been made for some of the components of the error. We propose an averaged characteristic for the error as the standard deviation obtained at discrete intervals of distance. A version for practical use of these results is considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. A. A. Vinnitskii, Outline of the Foundations of Radar with Continuous Radio-Wave Emission [in Russian], Sov. Radio, Moscow (1961).

    Google Scholar 

  2. Ya. D. Shirman (ed.), Theoretical Foundations of Radar [in Russian], Sov. Radio, Moscow (1970).

    Google Scholar 

  3. I. S. Gonorovskii, Radio Engineering Circuits and Signals [in Russian], Radio Svyaz’, Moscow (1986).

    Google Scholar 

  4. V. D. Zakharchenko and A. A. Bryshin, Radar, Navigation, Communication, in: Abstracts Sixth International Scientific-Technical Conference, Voronezh, [in Russian], Vol. 1, 391 (2000).

    Google Scholar 

  5. F. J. Harris, “On the use of windows for harmonic analysis with the discrete fourier transform,” IEEE Proc, 51–83, January (1978).

  6. A. V. Dvorkovich, Tsifr. Obr. Signalov, No. 2, 49 (2001).

  7. A. V. Dvorkovich, Tsifr. Obr. Signalov, No. 3, 13 (2001).

  8. I. F. Skolov and D. E. Vakman, Radiotekh. Elektron., No. 1, 46 (1958).

  9. G. Korn and T. Korn, Mathematical Handbook for Scientists and Engineers, McGraw-Hill, New York (1968).

    Google Scholar 

Download references

Authors
  1. V. V. Ezerskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. M. Davydochkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Izmeritel’naya Tekhnika, No. 2, pp. 21–25, February, 2005.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ezerskii, V.V., Davydochkin, V.M. Optimization of the Spectral Processing of the Signal of a Precision Distance Sensor Based on a Frequency Rangefinder. Meas Tech 48, 133–140 (2005). https://doi.org/10.1007/s11018-005-0111-3

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-005-0111-3

Key words

Search

Navigation