Abstract
For both non-redundant and redundant systems, the inverse kinematics (IK) calculation is a fundamental step in the control algorithm of fully actuated serial manipulators. The tool-center-point (TCP) position is given and the joint coordinates are determined by the IK. Depending on the task, robotic manipulators can be kinematically redundant. That is when the desired task possesses lower dimensions than the degrees-of-freedom of a redundant manipulator. The IK calculation can be implemented numerically in several alternative ways not only in case of the redundant but also in the non-redundant case. We study the stability properties and the feasibility of a tracking error feedback and a direct tracking error elimination approach of the numerical implementation of IK calculation both on velocity and acceleration levels. The feedback approach expresses the joint position increment stepwise based on the local velocity or acceleration of the desired TCP trajectory and linear feedback terms. In the direct error elimination concept, the increment of the joint position is directly given by the approximate error between the desired and the realized TCP position, by assuming constant TCP velocity or acceleration. We investigate the possibility of the implementation of the direct method on acceleration level. The investigated IK methods are unified in a framework that utilizes the idea of the auxiliary input. Our closed form results and numerical case study examples show the stability properties, benefits and disadvantages of the assessed IK implementations.
Similar content being viewed by others
1 Introduction
Kinematics calculation of robotic manipulators is a fundamental task in robot control, involving many issues such as numerical efficiency [21, 26]. In the case of direct kinematics, the position and orientation of the end-effector are determined based on the joint coordinates. If the joint space (or operational space) and the task space (or workspace), in which the end-effector is moving, have the same dimensions, there is no kinematic redundancy [4, 14, 16, 20]. In other words, the degrees of freedom (DoFs) of the manipulator exactly equals the necessary DoFs for performing the task. The system is called kinematically redundant, if there is higher number of DoFs than the dimensions of the task.
In practice, the desired position of the end-effector (tool-center-point) is prescribed and we try to find the corresponding joint coordinate values. This mapping from the task space to the joint space is called inverse kinematics (IK). Several methods exist in the literature to solve the IK problem with different approaches. These methods can be categorized as geometric level approaches, velocity level approaches and acceleration level approaches. Acceleration level resolution methods of the IK problem may improve the performance of redundant robots [13, 24] comparing to velocity level methods. There are alternatives for the position error compensation too [9, 10]. In this paper, our focus is on the stability, accuracy and efficiency of different combination of approaches used for IK.
Non-redundant cases were considered in our recent paper [22]. The present paper generalizes the theoretical details and the set of case examples for redundant cases.
1.1 The idea of auxiliary input in motion control
We formalize and classify the presented IK approaches in a rigorous way. To this end, we borrow the notion of the auxiliary input that is used in the feedback linearization of the dynamic equations of robotic manipulators, e.q. when computed-torque like control or inverse dynamics control is applied for trajectory tracking [26, 28]. We summarize here the theoretical background briefly based on the literature. Let us assume the equation of motion of the manipulator in the following general form
Here the vector of general coordinates is \(\mathbf {q}\), the mass matrix is \(\mathbf {M}(\mathbf {q})\), the inertial forces are represented by the vector \(\mathbf {C}(\mathbf {q},\dot{\mathbf {q}})\), the independent control inputs are collected in \(\mathbf {u}\) and the control input distribution matrix is \(\mathbf {H}(\mathbf {q})\). One obtains the closed loop system in the following linear form
if the control input \(\mathbf {u}\) is synthesized by using the formula
The typical choice of the so-called auxiliary input \(\tilde{\mathbf {v}}\), which appears in (3), realizes a proportional-derivative (PD) linear feedback control [26]:
The PD controller realized in (4) and the proper choice of the gain values \(\tilde{P}\) and \(\tilde{D}\) provide stable error dynamics (i.e. \((\mathbf {q}-\mathbf {q}^{\mathrm {d}}) \mapsto \mathbf {0}\)), when the desired trajectory \(\mathbf {q}^{\mathrm {d}}(t)\) is tracked. The tuning of the gain values is detailed in [26].
One can conclude that the auxiliary input \(\tilde{\mathbf {v}}\) is chosen with respect to a particular control goal in general. In analogue, we introduce the auxiliary input for IK.
1.2 Synthetization of the auxiliary input, goals
In the subsequent sections, the variety of IK algorithms is realized by means of different synthesis of the auxiliary input: the linear error feedback and an alternative approach which uses the idea of direct error elimination. Both concepts are investigated on velocity and acceleration level, resulting four alternatives: velocity level feedback, velocity level direct elimination, acceleration level feedback and acceleration level direct elimination methods (VF, VD, AF and AD respectively). Three out of the four (VF, VD and AF) variations can be found in the literature, and they are only reformulated in the framework of the auxiliary input. Furthermore, their stability analysis is carried out considering digital control (i.e. time-quantization) [12, 17]. Digital effects are quite important and the time-step length affects the stability properties. However, a very few studies conduct discrete-time stability analysis, e.g. [12] and continuous-time stability proofs are typical, e.g. [2].
The question naturally arises: why is not there direct error elimination approach on acceleration level? This fourth alternative (AD) has been proposed in our recent paper [22] for non-redundant cases. In the present paper, we generalize AD for redundancy and investigate its feasibility. The stability analysis is carried out in [22] for all VF, VD, AF and AD variations for non-redundant case. This discrete-time stability analysis is generalized for kinematic redundancy in the present paper.
2 Inverse kinematics calculation alternatives
Transferring the motion to the workspace from the joint space and vice versa is an essential component of motion control algorithms. In IK problems, the desired trajectory \(\mathbf {r}^\mathrm {d}(t):\mathbb {R}\mapsto \mathbb {R}^m\) of the tool-center-point (TCP) position (or end-effector position) is prescribed in the workspace in the case of position trajectory tracking task [4, 14, 16, 26]. The tracking error \(\mathbf {e}\) is introduced as
with \(\mathbf {r}(\mathbf {q}):\mathbb {R}^n\mapsto \mathbb {R}^m\). The term \(\mathbf {r}(\mathbf {q})\) in (5) maps the joint coordinates to the actual TCP position and it involves the geometric properties of the manipulator. The desired position \(\mathbf {r}^\mathrm {d}(t)\) is purely time dependent. The IK calculation aims to find the joint variable vector \(\mathbf {q}(t)\in \mathbb {R}^n\) that satisfies the error equation
Note that we do not need to restrict the IK calculations to position tracking. In general case, (5) may interpret any virtual geometric constraint equations, which are referred as servo-constraints or control-constraints in the literature [6,7,8, 18, 30, 32].
Essentially, we distinguish the kinematically not redundant case, when \(n=m\), and the redundant case, when \(n>m\). In the case of redundancy there is no unique IK solution; rather, motion optimization is carried out [3, 4, 14, 16, 20, 26, 29, 31].
For the geometric level approach, (6) is solved directly as a nonlinear algebraic problem, e.g. [25, 27]. Yet, geometric solution is not typical in practice due to the possibly high computational demand. Typically, the IK is solved on velocity [1, 20, 29] or acceleration level [13, 20, 24]. The numerical methods presented in this paper are realized in velocity and acceleration level.
2.1 Auxiliary input synthesis on velocity level
The velocity level implementation has the advantage that the unknown joint speed \(\dot{\mathbf {q}}\) appears in linear form. Hence, it’s calculation demands low computational capacity. After differentiating (6) with respect to time,
is obtained. Equation (7) must be satisfied by determining the solution for \(\dot{\mathbf {q}}\). The linear connection of the TCP velocity \(\dot{\mathbf {r}}\) and the joint speed is given by
where the Jacobian matrix \(\mathbf {J}\in \mathbb {R}^{m \times n}\) is obtained as \(\mathbf {J}(\mathbf {q}) = \nabla _{\mathbf {q}}\mathbf {r}\). The commanded joint speed is expressed from (9) as
where \(\mathbf {J}^{\dag }\) denotes the Moore-Penrose generalized inverse [5, 19, 20, 23] of the non-square Jacobian. The term \(\mathbf {v}_{\mathrm {v}}\) in (10) is the auxiliary input, i.e. it has the same role as \(\tilde{\mathbf {v}}\) in (3). Considering Eq. (8),
seems to be a natural choice for the auxiliary input. The problem is that this choice does not provide position error elimination \(\mathbf {e}\), although
is a requirement of IK methods. Therefore a variety of numerical implementations is established in the literature. Providing the possibility of the elimination of position errors, two alternatives for the choice of \(\mathbf {v}_{\mathrm {v}}\) are detailed and studied in the following sections.
Note that (10) might be extended depending on the control goal [3, 4, 14, 16, 20, 26, 29, 31]. On one hand, a scalar cost function \(\varphi =\dot{\mathbf {q}}^{\intercal }\mathbf {W}\dot{\mathbf {q}}\) is minimized when the generalized inverse incorporates the weight matrix \(\mathbf {W}\):
We assume \(\mathbf {W}\) to be identity \(\mathbf {I}\), which results the simplified formula \(\mathbf {J}^{\dag }=\mathbf {J}^{\intercal }(\mathbf {J}\,\mathbf {J}^{\intercal })^{-1}\). On the other hand, the null-space \(\mathbf {N}_{\mathbf {J}}=\mathbf {I}-\mathbf {J}^{\dag }\mathbf {J}\) of the Jacobian is often used in order to minimize a scalar cost function \(\gamma (\mathbf {q})\). Then the joint speed is obtained as \(\dot{\mathbf {q}} = \mathbf {J}^{\dag } \mathbf {v}_{\mathrm {v}} + \mathbf {N}_{\mathbf {J}} \dot{\varvec{\xi }}\) with \(\varvec{\xi } = \nabla _{\mathbf {q}} \gamma\). In this paper, \(\gamma (\mathbf {q}) = 0\) is assumed.
2.1.1 Velocity level linear feedback approach (VF)
The present IK calculation alternatives differ in the synthesis of the auxiliary input \(\mathbf {v}_{\mathrm {v}}\) that appears in (10). The TCP position error is eliminated by using \(\mathbf {v}_{\mathrm {v}} := \dot{\mathbf {r}}^\mathrm {d} - \kappa (\mathbf {r}-\mathbf {r}^{\mathrm {d}})\), [29] with which we obtain the commanded joint speed as
By substituting (14) into (9), the TCP velocity arises in the form
Equation (15) shows that the error dynamics is stable for the scalar gain parameter \(\kappa >0\). By neglecting the digital effects [17], the following first order ordinary differential equation describes the error dynamics
of with the exponentially decaying solution is \(\mathbf {e}(t) = \mathbf {B} \mathrm {e}^{- \kappa t}\). We detail the stability analysis and the proper choice of \(\kappa\) in Sect. 3.1 in the presence of time-quantization.
2.1.2 Velocity level direct error elimination approach (VD)
Comparing to the VF method, the auxiliary input \(\mathbf {v}_{\mathrm {v}}\) (see: (10)) is synthesized in an alternative way. The fundamental goal is the direct elimination of the tracking error by a proper choice of the \(\mathbf {v}_{\mathrm {v}}\) [9, 10].
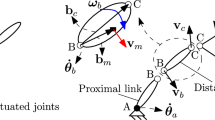
The actual values of the joint variables and the TCP position in the current time instance \(t_i\) are introduced as: \(\mathbf {q}_{i}:=\mathbf {q}(t_i)\), \(\mathbf {r}_{i}:=\mathbf {r}(\mathbf {q}(t_i))\) and \(\mathbf {r}^{\mathrm {d}}_{i}:=\mathbf {r}^{\mathrm {d}}(t_i)\). These variables and the time-step \(h:=t_{i+1}-t_{i}\) are shown in Fig. 1 left panel. Let us take the difference \(\varvec{\delta }_{i} = \mathbf {r}^{\mathrm {d}}_{i+1} - \mathbf {r}_{i}\) of the actual and the desired TCP position respectively in the current time instant \(t_i\) and upcoming time instant \(t_{i+1}\). The goal is to express the joint position increment directly with \(\varvec{\delta }_{i}\). Since the time-step \(h<<1\) is small, constant TCP velocity is assumed \(\dot{\mathbf {r}}_i\). We assume that considering the yet unknown velocity \(\dot{\mathbf {r}}_i\), the upcoming desired TCP position \(\mathbf {r}^{\mathrm {d}}_{i+1}\) is reached:
The TCP velocity \(\dot{\mathbf {r}}_{i}\) is expressed from (17). Indeed, the error \(\mathbf {e}_{i+1}=\mathbf {r}^{\mathrm {d}}_{i+1}-\mathbf {r}_{i+1}\) is approximately eliminated if the auxiliary input in the time instant \(t_i\) is synthesized as \(\mathbf {v}_{\mathrm {v}, i} = (\mathbf {r}^{\mathrm {d}}_{i+1}-\mathbf {r}_{i})/h\). Substituting the auxiliary input into (10), the commanded joint speed is obtained as
The commanded joint position in the upcoming time is directly expressed by applying the single explicit Euler [11] integration formula (\(\mathbf {q}_{i+1}=\mathbf {q}_{i} + h \dot{\mathbf {q}}_i\)):
The TCP position error is shown in the right panel of Fig. 1. The TCP positioning error \(\mathbf {e}_{i+1}\) occures, because the relation of the joint coordinates and the TCP position is nonlinear. However, if \(\mathbf {r}(\mathbf {q})\) is linear, then \(\mathbf {e}_{i+1}=\mathbf {0}\) is achieved. In general, the error \(\mathbf {e}_{i+1}\) converges to zero for the time-step \(h \mapsto 0\). The convergence analysis is detailed in Sect. 3.1.
The advantage of the direct error elimination method over the linear feedback approach is that the joint position increment (see: (19)) is obtained directly, and there is no need for considering the joint or TCP speed. Furthermore, the joint position increment is directly related to the TCP positioning error.
2.2 Auxiliary input synthesis on acceleration level
The IK problem is maintained on acceleration level in some cases, e.g. [13, 24]. We gain the acceleration level error equation after time differentiating (6) twice:
Equation (21) needs to be satisfied in the acceleration level approaches. Similarly to (9), we express the TCP acceleration
Since the joint acceleration is linear in (22), the commanded joint acceleration is expressed as:
where \(\mathbf {v}_{\mathrm {a}}\) is again the auxiliary input of the IK control. Considering Eq. (21), one could synthesize the auxiliary input as
The stable position error dynamics is not guaranteed by (24). To avoid this problem, a variety of the synthesis of \(\mathbf {v}_{\mathrm {a}}\) is applied in the literature. Similarly to the velocity level approaches, two variations for the choice of \(\mathbf {v}_{\mathrm {a}}\) are detailed in the following sections, which are capable of the positioning error elimination.
2.2.1 Acceleration level linear feedback approach (AF)
By chosing the proper gain parameters \(\kappa _{\mathrm {P}}\) and \(\kappa _{\mathrm {D}}\), the auxiliary input \(\mathbf {v}_{\mathrm {a}} := \ddot{\mathbf {r}}^\mathrm {d} - \kappa _{\mathrm {D}} (\dot{\mathbf {r}}-\dot{\mathbf {r}}^{\mathrm {d}}) - \kappa _{\mathrm {P}} (\mathbf {r}-\mathbf {r}^{\mathrm {d}})\) provides the elimination of the TCP tracking error [13]. The auxiliary input is substituted in Eq. (23) and we obtain the commanded joint acceleration as
By substituting (25) into (22), the TCP acceleration can be expressed as:
which leads to a stable error dynamics with the scalar gain parameters \(\kappa _{\mathrm {P}}>0\) and \(\kappa _{\mathrm {D}}>0\) governed by the second order differential equation
The error dynamics is asymptotically stable, if \(\kappa _{\mathrm {P}} > 0\) and \(\kappa _{\mathrm {D}} > 0\) and we assume continuous dynamics. However, the digital effects [12, 17] are important. The stability analysis and the choice of \(\kappa _{\mathrm {P}}\) and \(\kappa _{\mathrm {D}}\) are demonstrated in Sect. 3.1 in the presence of the discrete dynamical effects due to digital control.
2.2.2 Acceleration level direct error elimination approach (AD)
Although the description of the IK methods in Sects. 2.1.1, 2.1.2 and 2.2.1 can be found the literature, they typically appear without using the framework of the auxiliary inputs. The method explained in the present Section was proposed first in [22] and here it is generalized for redundant cases. The goal is the direct elimination of the position error by choosing the auxiliary input appearing in (23) properly. The method explained here is the acceleration level analogy of the velocity level direct error elimination (VD) method.
The deviation \(\varvec{\delta }_{i} = \mathbf {r}^{\mathrm {d}}_{i+1} - \mathbf {r}_{i}\) between the realized and the prescribed TCP position is considered, in analog to the VD approach, as it is shown in Fig. 2. By the proper choice of the constant TCP acceleration \(\ddot{\mathbf {r}}_i\), the TCP position prescribed in the upcoming time instant \(\mathbf {r}^{\mathrm {d}}_{i+1}\) is reached:
The error \(\varvec{\delta }_{i}\) is approximately eliminated if the auxiliary input is chosen as \(\mathbf {v}_{\mathrm {a}, i} = 2(\mathbf {r}^{\mathrm {d}}_{i+1}-\mathbf {r}_{i})/h^2 - 2 \dot{\mathbf {r}}_{i}/h\). This formula is obtained by the solution (28) for the unknown acceleration \(\ddot{\mathbf {r}}_{i}\). By substituting \(\mathbf {v}_{\mathrm {a}, i}\) into (23) and applying (9) for the actual time instant (\(\dot{\mathbf {r}}_{i} = \mathbf {J}_i \dot{\mathbf {q}}_i\)), and introducing the joint speed approximation \(\dot{\mathbf {q}}_i \approx \mathbf {J}^{\dag }(\mathbf {r}^{\mathrm {d}}_{i+1}-\mathbf {r}_{i})/h\), the commanded joint acceleration
can be synthesized. In order to obtain explicit formula for the joint position, one-step time integration is carried out. First, the velocity and after that the joint position is expressed with the Adams–Moulton family of numerical integrators [11]:
We directly obtain the upcoming commanded joint position. Again, small TCP position error \(\mathbf {e}_{i+1}\) arises because of the nonlinearity of \(\mathbf {r}(\mathbf {q})\); however, \(\mathbf {e}_{i+1}\) converges to zero when \(h \mapsto 0\). The results of the convergence analysis are presented in Sect. 3.1.
In analogy with the VD approach, the increment of the joint position vector is obtained without including the joint or TCP acceleration in the formulae.
3 Convergence analysis and case study examples
Figure 3 shows the case study examples in a systematic order. The analytical convergence analysis and its general results are shown first, then the numerical case examples show that the analytically obtained general conclusions are correct. The strength of the presented stability analysis is that time-quantization is considered, and the stable parameter set is determined in terms of the time-step length h.
3.1 Convergence analysis
We couldn’t find the rigorous stability analysis and comparison of the presented four IK methods in the presence of digital effects. The stability analysis of the four methods (VF, VD, AF and AD) is carried out by the time integration (if necessary) and linearization (for nonlinear case examples) of the commanded joint position/speed/acceleration formulae (14), (19), (25) and (29). The linearization is carried out around an arbitrarily chosen configuration \(\mathbf {q}_0\). In each case, we obtain the discrete mappings [15]
that map the commanded joint variables from the time instant \(t_i\) to \(t_{i+1}\). In the case of the VD approach, the joint positions are mapped only. Although the mapped variables \(\mathbf {x} = [\mathbf {q}^{\intercal }; \dot{\mathbf {q}}^{\intercal }]^{\intercal }\) include the joint speed too in the case of the VF and AD methods. For the AF approach, the joint acceleration is also included in \(\mathbf {z} = [\mathbf {q}^{\intercal }; \dot{\mathbf {q}}^{\intercal }; \ddot{\mathbf {q}}^{\intercal }]^{\intercal }\). The coefficient matrix \(\mathbf {A}\) and the vector \(\mathbf {b}\) change depending on the formulae for the auxiliary input \(\mathbf {v}_{\mathrm {v}}\) or \(\mathbf {v}_{\mathrm {a}}\) and on the integration scheme. The eigen-values of \(\mathbf {A}\) define the convergence: \(|\lambda _i| < 1; \forall i\) guarantees asymptotic stability [15], defined in (12). The eigen-value analysis of each particular method is summarized in Sect. 3.1.5.
It was shown in our recent paper [22] that the matrix \(\mathbf {A}\) for models B and C are identical. It was also shown that the matrix \(\mathbf {A}\) for models B and C have the same pattern as for model A, but the pattern is repeated twice. It is because the workspace is two-dimensional instead of one. As a consequence, the mapping matrix is shown only for the models A and D with one-dimensional workspace.
Case study examples: non-redundant case example models (A, B and C) are in the left column, redundant case example models (D, E and F) are in the right column. In the top row, the simplest possible nonlinear cases (A and D) are considered: the function \(r(\mathbf {q})\) maps the joint variables to the one-dimensional workspace. Linear and nonlinear models with two-dimensional workspace are depicted in the middle and the bottom rows (B, E, and C and F respectively)
3.1.1 Convergence analysis of the VF approach
In the VF approach, the numerical integration scheme was the second order Adams–Bashforth scheme [11]:
This integration scheme is applied on the commanded joint velocity defined in (14), with which the mapping matrix is obtained in the form below for the model A and configuration \(q_0=0\):
Note that the matrix \(\mathbf {A}_{\mathrm {VF}}\) repeats the same pattern for models B and C. Indeed, the eigen-values are also the same, but multiple. The real eigen-values of \(\mathbf {A}_{\mathrm {VF}}\) are
In redundant case (model D) with \(\mathbf {q}_0=\mathbf {0}\), the mapping matrix is obtained as:
of which the eigen-values are \(\lambda _{v1}\), \(\lambda _{v2}\), 0 and 1. The new 0 and 1 eigen-values, which appear because of the redundancy, are spurious eigen-values; i.e. the 1 eigen-value does not mean that the system is marginally stable. The stable region is plotted in the left chart of Fig. 4. The choice of the time-step h and the gain parameter \(\kappa\) inside the stable region (yellow) guarantees the decay of the tracking error \(\mathbf {e}\). Note that the stable region has infinitely long but monotonically narrowing tails both in the direction of the time-step duration h and in the direcion of the gain parameter \(\kappa\).
3.1.2 Convergence analysis of the VD approach
The numerical integration is already incorporated into the commanded joint position formula defined in (19). The mapping matrix for model A with \(q_0=0\) reads:
of which the eigen-value is always zero, indeed. For models B and C with two-dimensional workspace, the matrix is 2 by 2 zero matrix, i.e. the pattern is repeating itself again. For the redundant case (model D) with \(\mathbf {q}_0=\mathbf {0}\), the mapping matrix is:
The redundancy introduces one extra row and column for each extra DoF, and as a consequence, a new spurious eigen-value 1 appears. The exponential convergence of the tracking error to zero is always guaranteed.
3.1.3 Convergence analysis of the AF approach
Model A is considered again with \({q}_0={0}\). In case of the acceleration level feedback IK approach, the integration scheme was the second order Adams–Bashforth scheme combined with the second order Adams–Moulton scheme [11]:
This integration scheme is applied on the commanded joint acceleration defined in (25) with which, the mapping matrix reads
The real eigen-value \(\lambda _{a1}(\kappa _{\mathrm {P}},\kappa _{\mathrm {D}},h)\) and the complex eigen-values \(\lambda _{a2}(\kappa _{\mathrm {P}},\kappa _{\mathrm {D}},h)\), \(\lambda _{a3}(\kappa _{\mathrm {P}},\kappa _{\mathrm {D}},h)\) of \(\mathbf {A}_{\mathrm {AF}}\) can be obtained in closed form; however, we do not show the resulting formula because of its high complexity.
In the redundant case, when model D is investigated, the mapping matrix arises in the form:
Besides the eigen-values \(\lambda _{a1}\), \(\lambda _{a2}\) and \(\lambda _{a3}\), additional three eigen-values 0, 1, 1 appear for each extra DoF. The stable region in the parameter space is shown in the right panel of Fig. 4. The choice of parameters inside the stable region (yellow) guarantees the decay of the tracking error \(\mathbf {e}\). There is no stable region for the gain value \(\kappa _{\mathrm {D}}=0\); although increasing \(\kappa _{\mathrm {D}}\) modifies the shape of the stable region. The most important difference comparing to the stability chart of the VF method is that the maximum time interval h is limited.
Stable domains of the gain parameters and the time-step. Left panel: stable region of the parameters \(h [\mathrm {s}]\) and \(\kappa [1/\mathrm {s}]\) in the case of the velocity level linear feedback (VF) method. The relevant region is zoomed. Right panel: stable region of the parameters \(h [\mathrm {s}]\), \(\kappa _{\mathrm {D}} [1/\mathrm {s}]\) and \(\kappa _{\mathrm {P}} [1/\mathrm {s}^2]\) in the case of the acceleration level feedback (AF) method. The scale of h in the vertical axis is the same in the two charts
A very important observation about the linear feedback approaches is that Fig. 4 clearly shows that the stable region for the time-step h and the proportional gains \(\kappa\) and \(\kappa _{\mathrm {P}}\) is much larger for the acceleration level approach than for the velocity level one. The practically important benefit is that larger time-steps are allowed without loosing stability.
3.1.4 Convergence analysis of the AD approach
Model A and \({q}_0={0}\) is investigated first. The commanded acceleration is defined by (29), and the numerical integration scheme is defined in (30) and (31), with which the mapping matrix is:
of which the eigen-values are 0 and \(-1\) for any time-step h. This two-element eigen-value set is multiple for each dimension of the workspace. For the redundant case (model D with \(\mathbf {q}_0=\mathbf {0}\)), the mapping matrix is
of which the eigen-value set extends with two spurious 1 eigen-value for each extra DoF. The new spurious eigen-values do not change the fact that the zero error solution is marginally stable because of the \(-1\) eigen-value. In practice \(-1\) eigen-value causes a non-decaying timestep-by-timestep numerical oscillation.
3.1.5 Summary on the convergence analysis
For all the A, B, C, D, E, and F case examples, the same stability chart is valid for the velocity and acceleration level linear feedback approaches (VF and AF) (see: Fig. 4). Two parameters, namely h and \(\kappa\) determine the convergence for the VF method, while the convergence of the AF method is determined by h, \(\kappa _{\mathrm {P}}\) and \(\kappa _{\mathrm {D}}\). The convergence of method VD is guaranteed, since the non-spuriois eigen-values are always zeros. Method AD is proven to be marginally stable, since there is always an eigen-value, which is \(-1\). The eigen-value sets are summarized for each IK method in Table 1. In redundant case, the number of eigen-values is 2m, m, 3m and 2m respectively for the VF, VD, AF and AD methods. The number of eigen-values introduced by the redundant extra DoFs is \(2(n-m)\), \(n-m\), \(3(n-m)\), \(2(n-m)\) respectively. The case examples in the subsequent section show that the eigen-value analysis and the numerical simulations are in correspondence. In each case, both stable parameter sets and parameter sets from the vicinity of the stability border were tested.
3.2 Case examples A and D
Case example models A and D (see Fig. 3) are the simplest possible ones in the sense that the workspace is \(m=1\) dimensional. If there is no redundancy, \(n=1\). However, for redundant case \(n>m\) must be true, which yields \(n=2\) DoF in the simplest case. We consider a nonlinear mapping from the \(\mathbb {R}^1\) or \(\mathbb {R}^2\) joint space to the \(\mathbb {R}^1\) workspace without any particular physical meaning.
3.2.1 Kinematically non-redundant case: model A
The nonlinear function r(q) and the desired TCP position are given. The desired TCP trajectory \(r^{\mathrm {d}}(t)\) and the function r(q), which maps from the joint space to the workspace, were
in the numerical simulations and also in the analytical convergence analysis. The parameter values were \(a_0=1\,\mathrm {m}\), \(a_1=1\,\mathrm {m}\), \(\omega =1\,\mathrm {rad/s}\) and \(c=0.2\,\mathrm {m}\). The simulations were performed with an initial error as it is shown in the top panels of Fig 5. The gain parameters and the time-step were \(\kappa =19\,1/\mathrm {s}\), \(\kappa _{\mathrm {P}}=250\,1/\mathrm {s}^2\), \(\kappa _{\mathrm {D}}=8\,1/\mathrm {s}\) and \(h=0.05\,\mathrm {s}\) respectively for the simulations that are carried out in the inner vicinity of the stability border shown in Fig. 4 (close to the marginal stability). A parameter set deep inside the stable region was \(\kappa =5\,1/\mathrm {s}\) and \(\kappa _{\mathrm {P}}=50\,1/\mathrm {s}\) without changing any other parameter. Note that every other simulation is carried out with the same gain parameters and time-step. The initial conditions are \(q_0=1\), \(\dot{q}_0=0\).
3.2.2 Kinematically redundant case: model D
The joint variables are mapped to the workspace by
Every other parameter is the same as in the non-redundant case example A. The initial conditions were \(\mathbf {q}_0 = [1; 1]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\). The simulation results are shown in the bottom panels of Fig 5. As we can see in the graphs for VF, and AF methods, the almost unstable parameter sets provide stability; however the error decays very slowly with high oscillations. The convergence speeds up when choosing the parameters from deep inside the stable range. Method VD suppresses the error quickly, but method AD causes abrupt peaks in the position error. We expected this kind of stability problem based on the eigen-value analysis.
Position error \(e=r(\mathbf {q})-r^d(t)\) for the case study examples A (top row) and D (bottom row). Methods VF and AF are shown in the left and the middle column with the almost unstable and the stable parameter set respectively. The right column shows the error for the VD and the AD methods, for which there is no parameter which affect the stability
3.3 Case examples B and E
The non-redundant and the redundant cases were tested on the linear models B and E. Models B and E are a bit more general than A and D, since the workspace is not one-dimensional. The \(\mathbb {R}^2 \mapsto \mathbb {R}^2\) and \(\mathbb {R}^3 \mapsto \mathbb {R}^2\) linear mapping functions for the planar PP and PPP manipulators, which consist of two and three perpendicular prismatic drive (see: Fig. 3), are respectively
where \(l=1\,\mathrm {m}\) is a geometric parameter. The desired path was a circle defined by
with parameters \(a_0=1 \, \mathrm {m}\), \(a_1=0.5 \, \mathrm {m}\) and \(\omega =2 \, \mathrm {rad/s}\). For model B, the initial conditions were \(\mathbf {q}_0 = [0.5; 0.5]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\). For model E, the initial conditions were set to \(\mathbf {q}_0 = [0; 0; 0]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\).
First, we carried out numerical simulations with parameters intentionally chosen from the border of the stable range; i.e. the norm of the eigen-values of \(\mathbf {A}\) is about 1 (for the IK parameter values see: Sect. 3.2.1). The Euclidean norm of the TCP positioning error is shown in Fig. 6. The behaviour of the IK methods is similar to the previous case examples A and D. However, models B and E are linear. Because of the linearity, methods VD and AD are able to track the given trajectory without error. Fig. 7 depicts the desired and the realized path of the TCP. The vibrations in the vicinity of the stability border are clear for VF and AF (left column). However stable parameters provide smooth decaying of the tracking error (middle column). Although the direct methods practically jump to the desired path, in the physical reality, the motion controller and the actuators limit the speed of this motion.
The Euclidean error norm \(\left\| \mathbf {e} \right\| = \left\| {\mathbf {r}}(\mathbf {q}) - \mathbf {r}^d(t) \right\|\) for the case example models B (top row) and E (bottom row). Almost unstable and stable cases for VF and AF approaches and the results for VD and AD methods are shown in separate columns
The desired \(\mathbf {r}^d(t)\) and the realized trajectory \({\mathbf {r}}(\mathbf {q})\) of the TCP for the case example models B (top row) and E (bottom row). Close-to-unstable and stable cases for VF and AF approaches and the results for VD and AD methods are shown in separate columns. The initial positions are shown by larger markers
3.4 Case examples C and F
Nonlinear non-redundant and redundant models (C and F respectively) are taken as case examples. Models C and F are planar RR and RRR manipulators. The joint variables are mapped to the TCP position by the following \(\mathbb {R}^2 \mapsto \mathbb {R}^2\) and \(\mathbb {R}^3 \mapsto \mathbb {R}^2\) functions
where \(l=1\,\mathrm {m}\) is the length of the bars and the abbreviations are \(c_i = \cos (q_i)\), \(s_i = \sin (q_i)\). For model C, the initial conditions were \(\mathbf {q}_0 = [22.5; 81]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\) for methods VF, VD, AF and \(\mathbf {q}_0 = [30.5; 81]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\) for method AD. For model F, the initial conditions were \(\mathbf {q}_0 = [-10; 48; 132]^{\intercal }\) and \(\dot{\mathbf {q}}_0 = \mathbf {0}\) for methods VF, VD, AF and \(\mathbf {q}_0 = [-1; 48; 132]^{\intercal }\) for method AD. Method AD is very sensitive to any large initial error, that is the reason for choosing different initial conditions.
The Euclidean error norm \(\left\| \mathbf {e} \right\| = \left\| {\mathbf {r}}(\mathbf {q}) - \mathbf {r}^d(t) \right\|\) for the case example models C (top row) and F (bottom row). Almost unstable and stable cases for VF and AF approaches and the results for VD and AD methods are shown in separate columns
The desired \(\mathbf {r}^d(t)\) and the realized trajectory \({\mathbf {r}}(\mathbf {q})\) of the TCP for the case example models C (top row) and F (bottom row). Close-to-unstable and stable cases for VF and AF approaches and the results for VD and AD methods are shown in separate columns. The initial positions are shown by larger markers
Simulations with close-to-unstable and stable parameters were carried out. For the parameters \(\kappa\), \(\kappa _{\mathrm {P}}\), \(\kappa _{\mathrm {D}}\), h and for the desired trajectory see Sect. 3.2.1 and Eq. (53). In the case of these nonlinear example models, the behavior is a bit more intricate then for cases B and E. As we can see in Fig. 8, there is a small positioning error remaining for IK methods VF and AF because of the nonlinearity. Again, method AD develops oscillations after settling down (right, bottom panel). This phenomena questions the practical applicability. Fig. 9 shows the desired and the realized trajectories.
4 Conclusion
Four alternatives for the numerical implementation of the inverse kinematics calculation were studied: the feedback approach and the direct error elimination approach were implemented on velocity and acceleration level in the framework of auxiliary inputs. The comparison of the stability properties were carried out and the stable parameter regions were presented, which are essential in the practical application of these algorithms. The acceleration level feedback method is proven to be beneficial over the velocity level type in the sense that the stable parameter region is larger and therefore larger time-step is allowed in the digital implementation. In order to test the possible benefits of acceleration level methods, we introduced the acceleration level direct error elimination method (AD).
The analytical convergence analysis showed that VF, VD, AF methods are convergent and therefore feasible in practice. The stable parameter range was defined for VF and AF methods. It was however proven that the AD method is marginally stable, which means that its practical application is not feasible in the present form. Some research is worth being carried out on the possibilities of stabilization, because the convergence of the AD method is much faster than the AF feedback method when the underlying system is linear. The analytically obtained stability charts were tested by numerical case example simulations, and the behavior was as one could expect based on the stability charts.
References
An S, Lee D (2019) Prioritized inverse kinematics: generalization. IEEE Robot Autom Lett 4(4):3537–3544. https://doi.org/10.1109/lra.2019.2927945
Antonelli G (2009) Stability analysis for prioritized closed-loop inverse kinematic algorithms for redundant robotic systems. IEEE Trans Robot 25(5):985–994. https://doi.org/10.1109/tro.2009.2017135
Baillieul J (1985) Kinematic programming alternatives for redundant manipulators. In: Proceedings of the IEEE conference robotics and automation, pp 722–728. https://doi.org/10.1109/ROBOT.1985.1087234
Baker DR, Wampler CW (1988) On the inverse kinematics of redundant manipulators. Int J Robot Res 7(2):3–21. https://doi.org/10.1177/027836498800700201
Ben-Israel A, Greville TNE (2003) Generalized inverses: theory and applications, 2nd edn. Springer, New York. ISBN 9780387216348
Blajer W, Kolodziejczyk K (2004) A geometric approach to solving problems of control constraints: theory and a dae framework. Multibody Syst Dyn 11(4):343–364. https://doi.org/10.1023/B:MUBO.0000040800.40045.51
Blajer W, Kolodziejczyk K (2008) Modeling of underactuated mechanical systems in partly specified motion. J Theor Appl Mech 46(2):383–394
Blajer W, Seifried R, Kolodziejczyk K (2015) Servo-constraint realization for underactuated mechanical systems. Arch Appl Mech 85(9–10):1191–1207. https://doi.org/10.1007/s00419-014-0959-2
Burrell T, Montazeri A, Monk S, Taylor CJ (2016) Feedback control-based inverse kinematics solvers for a nuclear decommissioning robot. IFAC-PapersOnLine 49(21):177–184. https://doi.org/10.1016/j.ifacol.2016.10.541
Buss SR (2004) Introduction to inverse kinematics with jacobian transpose, pseudoinverse and damped least squares methods. IEEE J Robot Autom Tech Rep
Butcher J (2008) Numerical methods for ordinary differential equations. Wiley, Hoboken. ISBN 978-0-470-72335-7
Das H, Slotine J, Sheridan TB (1988) Inverse kinematic algorithms for redundant systems. In: IEEE international conference on robotics and automation, pp 43–48. Philadelphia. https://doi.org/10.1109/ROBOT.1988.12021
De Luca A, Oriolo G, Siciliano B (1992) Robot redundancy resolution at the acceleration level. Lab Robot Autom 4(2):97–106
From PJ, Gravdahl JT (2007) General solutions to functional and kinematic redundancy. In: Proceedings of the 46th IEEE conference on decision and control, pp 1–8. New Orleans. ISSN: 0191-2216. https://doi.org/10.1109/CDC.2007.4434442
Guckenheimer J, Holmes P (1983) Nonlinear oscillations. In: Dynamical systems and bifurcations of vector fields. Springer, New York. ISBN 978-1-4612-7020-1
Hollerbach JM, Suh KC (1987) Redundancy resolution of manipulators through torque optimization. IEEE J Robot Autom 3(4):308–316. https://doi.org/10.1109/JRA.1987.1087111
Kirgetov VI (1996) Micro-chaos in digital control. J Nonlinear Sci 6(5):415–448. https://doi.org/10.1007/BF02440161
Kirgetov VI (2019) The motion of controlled mechanical systems with prescribed constraints (servoconstraints). PMM 31(3):433–446. https://doi.org/10.1016/0021-8928(67)90029-9
Moore EH (1920) On the reciprocal of the general algebraic matrix. Bull Am Math Soc 26(9):394–395
Nakamura Y (1991) Advanced robotics: redundancy and optimization. Addison-Wesley, Reading
Orin DE, Schrader WW (1984) Efficient computation of the Jacobian for robot manipulators. Int J Robot Res 49(21):66–75. https://doi.org/10.1177/027836498400300404
Patkó D, Zelei A (2019) Alternative inverse kinematic calculation methods in velocity and acceleration level. In: Awrejcewicz J, Kazmierczak M, Mrozowski J (ed) Theoretical approaches in non-linear dynamical systems-DSTA 2019, pp 405–418. Lodz, Poland
Penrose R, Todd JA (1955) A generalized inverse for matrices. Math Proceed Cambridge Philos Soc 51(3):406–413. https://doi.org/10.1017/s0305004100030401
Reiter A, Müller A, Gattringer H (2018) On higher-order inverse kinematics methods in time-optimal trajectory planning for kinematically redundant manipulators. IEEE Trans Ind Inf 14(12):1681–1690. https://doi.org/10.1109/TII.2018.2792002
Sharma S, Kraetzschmar G, Scheurer C, Bischoff R (2012) Unified closed form inverse kinematics for the KUKA youBot. Proc ROBOTIK 2012 - 7th German Conference on Robotics. Munich, Germany, pp 1–6
Siciliano B, Khatib O (2008) Handbook of robotics. Springer, New York. ISBN 978-3-540-38219-5
Sinha A, Chakraborty N (2019) Geometric search-based inverse kinematics of 7-dof redundant manipulator with multiple joint offsets. In: International conference on robotics and automation (ICRA), pp 5592–5598. https://doi.org/10.1109/icra.2019.8793725
Spong MW, Vidyasagar M (1989) Robot dynamics and control. Wiley, Hoboken
Wang J, Li Y, Zhao X (2010) Inverse kinematics and control of a 7-DOF redundant manipulator based on the closed-loop algorithm. Int J Adv Robot Syst 7(4):1–10. https://doi.org/10.5772/10495
Yang Y, Betsch P, Altmann R (2015) A numerical method for the servo constraint problem of underactuated mechanical systems. PAMM Proc Appl Math Mech 15(1):79–80. https://doi.org/10.1002/pamm.201510030
Yoshikawa T (1984) Analysis and control of robot manipulators with redundancy. In: Robotics Research: The First International Symposium, pp 735–747
Zelei A, Kovács LL, Stépán G (2011) Computed torque control of an under-actuated service robot platform modeled by natural coordinates. Commun Nonlinear Sci Numer Simul 16(5):2205–2217. https://doi.org/10.1016/j.cnsns.2010.04.060
Acknowledgements
The research reported in this paper and carried out at BME has been supported by the Hungarian National Research, Development and Innovation Office (NKFI-FK18 128636), by the Hungarian-Chinese Bilateral Scientific and Technological cooperation Fund (2018-2.1.14-TET-CN-2018-00008) and by the NRDI Fund (TKP2020 IES,Grant No. BME-IE-BIO and TKP2020 NC, Grant No. BME-NC) based on the charter of bolster issued by the NRDI Office under the auspices of the Ministry for Innovation and Technology.
Funding
Open Access funding provided by Budapest University of Technology and Economics.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patkó, D., Zelei, A. Velocity and acceleration level inverse kinematic calculation alternatives for redundant manipulators. Meccanica 56, 887–900 (2021). https://doi.org/10.1007/s11012-020-01305-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-020-01305-z