Skip to main content
SpringerLink
Log in

Probabilistic and stochastic aspects of rubber hyperelasticity

  • Published:
Meccanica Aims and scope Submit manuscript

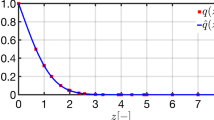
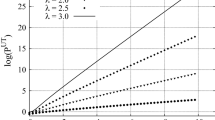
Abstract

The main aim of this work is to compare various models of rubber elasticity, i.e. neo-Hookean, Mooney-Rivlin, Yeoh, Gent, Arruda-Boyce as well as the Extended Tube model in terms of their application to the probabilistic analysis. Some discussions concerning failure analysis of the rubbers according to these models is provided also. Constitutive relations following these theories are tested for the case of uniaxial tension of the incompressible material, where deformation of a rubber specimen is treated as Gaussian random variable having a priori given expectation and standard deviations varying in some interval with bounds driven by various experimentation techniques. Probabilistic analysis is provided here in two alternative ways—via traditional Monte-Carlo technique as well as using higher order stochastic perturbation method implemented both in the symbolic computer algebra software. An application of non-Gaussian distributions relevant to the considered deformation, like lognormal one for instance has been also considered. This analysis includes computational determination of the first four basic probabilistic characteristics, i.e. expectation, coefficient of variation, skewness and kurtosis, and is provided to verify the resulting probabilistic distribution of the induced stress and its entropy. Some conclusions are drawn for the generalization of this method to other stress softening materials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Arruda EM, Boyce MC (1993) A three-dimensional model for the large stretch behavior of rubber elastic materials. J Mech Phys Solids 41(2):389–412

    Article  ADS  MATH  Google Scholar 

  2. Chaboche JL (2008) A review of some plasticity and viscoplasticity constitutive theories. Int J Plast 24:1642–1693

    Article  MATH  Google Scholar 

  3. Christensen RM (2010) Theory of viscoelasticity. Dover Publ, Dover

    Google Scholar 

  4. Dorfmann A, Ogden RW (2004) A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int J Solids Struct 4:1855–1878

    Article  MATH  Google Scholar 

  5. Gent AN (1996) A new constitutive relation for rubber. Rubber Chem Technol 69:59–61

    Article  Google Scholar 

  6. Guedri M, Lima AMG, Bouhaddi N, Rade DA (2010) Robust design of viscoelastic structures based on stochastic finite element models. Mech Syst Signal Proc 24(1):59–77

    Article  ADS  Google Scholar 

  7. Gutierrez MA, de Borst R (1999) Numerical analysis of localization using a viscoplastic regularization: influence of stochastic material defects. Int J Numer Methods Eng 44:1823–1841

    Article  MATH  Google Scholar 

  8. Harth T, Schwan S, Lehn J, Kollmann FG (2004) Identification of material parameters for inelastic constitutive models: statistical analysis and design of experiments. Int J Plast 20:1403–1440

    Article  MATH  Google Scholar 

  9. Heinrich G, Kaliske M (1998) Theoretical and numerical formulation of a molecular based constitutive tube-model of rubber elasticity. Comput Theor Polymer Sci 7:227–241

    Article  Google Scholar 

  10. Heinrich G, Straube E, Helmis G (1988) Rubber elasticity of polymer networks: theories. Adv Polymer Sci 85:33–87

    Article  Google Scholar 

  11. Jin T, Yu L, Yin Z, Xiao H (2014) Bounded elastic potentials for rubberlike materials with strain-stiffening effects. Z Angew Math Mech ZAMM 94:1–12

    Article  MATH  Google Scholar 

  12. Kaliske M, Heinrich G (2010) An extended tube-model for rubber elasticity: statistical-mechanical theory and finite element implementation. Rubber Chem Technol 72:602–632

    Article  Google Scholar 

  13. Kaliske M, Rothert H (1997) On the finite element implementation of rubber-like materials at finite strains. Eng Comput 14(2):216–232

    Article  MATH  Google Scholar 

  14. Kamiński M (2002) On probabilistic fatigue models for composite materials. Int J Fatigue 24(2–4):477–495

    Article  MATH  Google Scholar 

  15. Kamiński M (2013) The stochastic perturbation method for computational mechanics. Wiley, Chichester

    Book  MATH  Google Scholar 

  16. Kamiński M, Lauke B (2012) Probabilistic and stochastic analysis of the effective properties for the particle reinforced elastomers. Comput Mater Sci 56:147–160

    Article  Google Scholar 

  17. Kamiński M, Lauke B (2014) Probabilistic homogenization of polymers filled with rubber particles. Comput Mater Sci 82:483–496

    Article  MATH  Google Scholar 

  18. Mandel J, Roth FL, Steel MN, Stiehler RD (1959) Measurement of the aging of rubber vulcanizates. J Res Nat Bureau Stand–C: Eng Inst 63(2):141–145

    Google Scholar 

  19. Marckmann G, Verron E (2006) Comparison of hyperelastic models for rubber-like materials. Rubber Chem Technol 79:835–857

    Article  Google Scholar 

  20. Mooney M (1940) A theory of large elastic deformation. J Appl Phys 11(9):582–592

    Article  ADS  MATH  Google Scholar 

  21. Mott PH, Roland CM (2001) Aging of natural rubber in air and seawater. Rubber Chem Technol 74:79–88

    Article  Google Scholar 

  22. Mullins L (1947) Effect of stretching on the properties of rubber. J Rubber Res 16:275–289

    Google Scholar 

  23. Mullins L (1969) Softening of rubber by deformation. Rubber Chem Technol 42:339–362

    Article  Google Scholar 

  24. Ogden RW (1984) Non-linear elastic deformations. Dover Publ, Dover

    MATH  Google Scholar 

  25. Ogden RW, Roxburgh DG (1999) A pseudo-elastic model for the Mullins effect in filled rubber. Proc R Soc A 455:2861–2877

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Ostoja-Starzewski M (2005) Scale effects in plasticity of random media: status and challenges. Int J Plast 21:1119–1160

    Article  MATH  Google Scholar 

  27. Rivlin RS (1948) Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Phil Trans R Soc Lond Ser A: Math Phys Sci. 241(835):379–397

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Shannon CE (1948) A mathematical theory of communication. Bell Syst Technol J 27:379–423

    Article  MathSciNet  MATH  Google Scholar 

  29. Shen Y, Chandrashekhara K, Breig WF, Oliver LR (2004) Neural network based constitutive model for rubber material. Rubber Chem Technol 77:257–277

    Article  Google Scholar 

  30. Treloar LRG (1975) The physics of rubber elasticity. Clarendon Press, Oxford

    MATH  Google Scholar 

  31. Truesdell C, Noll W (2004) The non-linear field theories of mechanics, 3rd edn. Springer, Berlin

    Book  MATH  Google Scholar 

  32. Volokh KY (2010) On modeling failure of rubber-like materials. Mech Res Commun 37:684–689

    Article  MATH  Google Scholar 

  33. Volokh KY (2013) Review of the energy limiters approach to modeling failure of rubber. Rubber Chem Technol 86(3):470–487

    Article  Google Scholar 

  34. Yeoh OH (1993) Some forms of the strain energy function for rubber. Rubber Chem Technol 66(5):754–771

    Article  Google Scholar 

Download references

Acknowledgements

The first Author would like to acknowledge the research fellowship from Leibniz-Institut für Polymerforschung Dresden e.V. in Germany where this work has been partially completed. The Authors would like to declare that they both actively participated in preparation of any part of this work. It has been submitted nowhere else and any part of this work is entirely intellectual property of both Authors. The Authors would like to acknowledge a discussion of some ideas contained in this work with prof. G. Heinrich from IPF Dresden.

Author information

Authors and Affiliations

  1. Chair of Structural Reliability, Department of Structural Mechanics, Faculty of Civil Engineering, Architecture and Environmental Engineering, Technical University of Łódź, Al. Politechniki 6, 90-924, Łódź, Poland

    Marcin Kamiński

  2. Leibniz-Institut für Polymerforschung Dresden e.V, Hohe Strasse 6, 01069, Dresden, Germany

    Bernd Lauke

Authors
  1. Marcin Kamiński
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bernd Lauke
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcin Kamiński.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kamiński, M., Lauke, B. Probabilistic and stochastic aspects of rubber hyperelasticity. Meccanica 53, 2363–2378 (2018). https://doi.org/10.1007/s11012-018-0821-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-018-0821-7

Keywords

Search

Navigation