Abstract
A non-standard aspect of phase-field fracture formulations for pressurized cracks is the application of the pressure loading, due to the fact that a direct notion of the fracture surfaces is absent. In this work we study the possibility to apply the pressure loading through a traction boundary condition on a contour of the phase field. Computationally this requires application of a surface-extraction algorithm to obtain a parametrization of the loading boundary. When the phase-field value of the loading contour is chosen adequately, the recovered loading contour resembles that of the sharp fracture problem. The computational scheme used to construct the immersed loading boundary is leveraged to propose a hybrid model. In this hybrid model the solid domain (outside the loading contour) is unaffected by the phase field, while a standard phase-field formulation is used in the fluid domain (inside the loading contour). We present a detailed study and comparison of the \(\varGamma\)-convergence behavior and mesh convergence behavior of both models using a one-dimensional model problem. The extension of these results to multiple dimensions is also considered.
Similar content being viewed by others
1 Introduction
Over the last decade phase-field models for fracture [1,2,3,4]—which are closely related to traditional gradient-enhanced damage models [5]—have been successfully applied to a wide range of problems, such as dynamic fracturing [6,7,8,9], large deformation fracturing [10, 11], fracturing of electromechanical materials [12, 13], cohesive fracturing [14, 15], fracturing of thermo-elastic solids [16, 17] and many more. The primary advantage of these models is the flexibility with which complex fractures can be simulated, which is a result of the diffuse fracture representation and due to the fact that propagation laws generally follow naturally from energy minimization principles. However, compared to sharp fracture models, phase-field models require high-resolution computational grids in the vicinity of the fractures.
The flexibility of the phase-field framework with respect to the representation of complex fracture patterns is also exploited in the context of fluid-driven fracture propagations (see references below). These models are highly relevant in applications concerning flow in porous media such as hydraulic fracturing. A particularly interesting aspect of the extension of phase-field models to hydraulic fracturing is that the phase-field model not only represents the fracture in a diffuse sense, but also represents the fluid-flow domain.
Various phase-field formulations for fluid-driven fracture propagation have been developed over the last couple of years. In Bourdin et al. [18] a variational formulation for pressure-driven phase-field fracture propagation is considered, in which the work exerted by the pressure inside a crack on the fracture surface is accounted for by a volumetric body force. Crack growth is simulated by quasi-static incrementation of the fracture volume. Alternative formulations for fluid-driven fracture propagation have been developed by enriching a poro-mechanical formulation with a phase-field fracture representation, of which the works by Miehe et al. [19, 20], Mikelić, Wheeler et al. [21, 22], and Wilson et al. [23] are particularly noteworthy. The primary difference between the formulations in these works is the way in which the phase-field influences the flow and action of the fluid on the porous medium.
The above-mentioned models for pressure-loaded phase-field fractures all rely on indirect application of the fracture-surface loading, in the sense that the sharp loading boundary is represented by a phase field. This is a very natural approach in phase-field models, but it also inherently limits the capabilities of the developed models. The absence of a discrete fracture surface in the formulation impedes direct incorporation of a versatile fluid-flow model and fluid-solid interface conditions, and requires a reconstruction of the fracture opening for the fluid-flow model.
In this contribution we study the possibility to directly incorporate the sharp fracture surface pressure-loading in a phase-field fracture representation. The key idea behind this approach is to extract a contour from the phase field and to use it as a standard pressure-loading boundary. We present a detailed analysis for the solution behavior of this model, the behavior of which is intuitively troublesome. In terms of computational techniques, the essential novel ingredient in our approach is the loading-surface extraction routine, which is inspired by the segmentation technique developed in the context of the finite cell method for image-based analysis [24]. To ameliorate the complications associated with the imposition of the mechanical loads on the phase-field fracture, we propose a hybrid diffuse-sharp fracture model, which further exploits the computational capabilities of the finite cell techniques used for the loading-boundary reconstruction. Based on a model problem we present a detailed analysis of both models, which highlights the superior fracture opening approximation behavior of the hybrid model.
In this manuscript, we restrict ourselves to pressure-loaded pre-existing fractures. A detailed understanding of the model—in terms of dependence on the phase-field length scale parameter and discretization parameters—for such stable fractures is relevant in itself, but also a prerequisite for applying it to propagating fractures. To assess the properties of the models as a basis for fracture propagation, we study the behavior of the thermodynamic driving-force field, which is the essential model aspect in the context of fracture propagation. The study presented herein focuses on a constant pressure loading, but the presented results are generally valid for heterogeneous tractions along the fracture surface, thereby enabling enrichment of the model with more sophisticated fracture-loading models.
In Sect. 2 we introduce the sharp pressure-loaded fracture problem, along with its phase-field and hybrid model representations. In Sect. 3 we discuss the employed finite element discretization technique and interface-extraction technique. A detailed analysis of both the phase-field model and the hybrid model is presented for a one-dimensional model problem in Sect. 4. This analysis pertains to the convergence of the models to the sharp model for decreasing length scales, and to the convergence of the finite element solutions under mesh refinement. In Sect. 5 we consider a two-dimensional benchmark problem, for which we demonstrate how the observed behavior in one dimension translates to multiple dimensions. A three-dimensional problem is considered to demonstrate applicability of the models in a volumetric setting. Finally, conclusions are drawn in Sect. 6.
2 Pressure-loaded fracture model formulations
In this section we introduce the problem setup for a pressure-loaded fracture, after which we consider the phase-field model corresponding to this sharp problem representation. Moreover, we propose a hybrid model that mimics the phase-field model only in the part where it is relevant, i.e. in the vicinity of the fracture.
2.1 Sharp fracture formulation
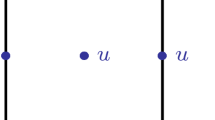
We consider an \(n_{\mathrm{dim}}\)-dimensional deformable solid \(\varOmega\) with external boundary \(\varGamma\) and an internal discontinuity boundary, \(\varGamma _{c}\), whose opposing sides are denoted by \(\varGamma _c^+\) and \(\varGamma _c^-\); see Fig. 1. The deformation of the solid is described by the displacement field \(\varvec{u}\). The external boundary is decomposed in a part, \(\varGamma _{D} \ne \emptyset\), on which Dirichlet conditions (prescribed displacements) are imposed, and a complementary part, \(\varGamma _N\), which is subject to Neumann conditions (prescribed traction). The outward pointing normal vector on the external boundary is denoted by \(\varvec{n}\). The opposing sides of the fracture surface \(\varGamma _{c}\), with outward-pointing (into the fluid domain) normal vectors \(\varvec{n}^+\) and \(\varvec{n}^-\), are loaded by a pressurized fluid with pressure p. Assuming small deformations and deformation gradients, the displacement of the solid under the influence of internal pressurization and in the absence of body forces is governed by:
The Cauchy stress tensor \(\varvec{\sigma }_e(\varvec{\varepsilon })\) is a function of the infinitesimal strain tensor \(\varvec{\varepsilon }=\nabla ^s \varvec{u}\), and \(\bar{\varvec{t}}\) and \(\bar{\varvec{u}}\) are the data for the Neumann and Dirichlet conditions, respectively.
Multiplication of the momentum balance in (1) with a test function and integration by parts yields the corresponding weak form problem:
In this formulation the trial space is defined as
which—modulo inhomogeneous boundary conditions—is also used as the test space \({\mathcal {V}}^{\varvec{u}}_0\). The jump operator acting on the normal component of the test function is defined as \(\llbracket v_n \rrbracket =(\varvec{v}^+-\varvec{v}^-)\cdot \varvec{n}\), where – in correspondence with the small deformations assumption—use is made of \(\varGamma _c=\varGamma _c^\pm\) and \(\varvec{n}=\varvec{n}^-=-\varvec{n}^+\). It is important to note here that in sharp fracture formulations a parametrization of the fracture boundaries is generally available. This parametrization is essential for the evaluation of the fracture surface integral in the weak form (2).
2.2 Phase-field fracture formulation
In the phase-field model for fracture the surface \(\varGamma _c\) is described by a phase (or damage) field, \(d:\varOmega \rightarrow [0,1]\), which approaches 1 at the center of the crack and vanishes far away from the fracture surface; see Fig. 2.
The surface area of the fracture is approximated by the functional
where \(l_0\) is a length-scale parameter that dictates the width of the smeared fracture, and where \(\left\| d \right\| _{S}\) is defined as the surface area measure. It has been proven that in the limit of the length scale going to zero, the diffuse fracture surface area converges to the sharp fracture surface area when the phase field satisfies the boundary value problem:
The equivalent weak form problem is given by
with the test and trial space being defined as \({\mathcal {V}}^d=H^1(\varOmega )\), with a constraint on d at \(\varGamma _c\).
The smeared elasticity problem associated with the phase-field description of the discrete fracture problem revolves around the idea of locally degrading the stiffness of the material through the phase field, which results—in its simplest form—in the redefinition of the Cauchy stress tensor as
where g(d) is a degradation function with properties \(g(0)=1\), \(g(1)=g^{\prime}(1)=0\), and \(\varvec{\sigma }_e\) is the stress associated with the undamaged, elastic, material. The vanishing derivative of g at \(d=1\) ensures that the fracture driving force vanishes upon completion of damage. The most common choice for the degradation function is \(g(d)=(1-d)^2\), which will also be considered in the remainder of this work. In order to restrict fracture propagation to tensile loading states, the stress degradation function is commonly merely applied to the tensile part of the stress tensor; see e.g. [2] for details.
Imposition of the pressure loading in the phase-field model is a non-standard aspect of the formulation, in the sense that it does not arise naturally as a volumetric term in the smeared problem. Fundamentally, the problem is that the phase-field formulation does provide a smeared representation of the fracture surface area, but that a direct notion of opposing sides of the fracture surface is lost. For that matter there is also no direct notion of a jump in the displacement field.
The absence of a direct notion of fracture opening can be resolved by approximating it in a smeared sense. Following the derivations by Chambolle [25, 26] in Bourdin et al. [18] the fracture volume increase is approximated as \(\int _\varOmega \varvec{u} \cdot \nabla d \,dV\) (conceptually, the jump is obtained by integrating perpendicular to the crack), whereas the fracture jump in References [19, 20, 23] is reconstructed using the stretch of the deformed material. Differences exists between the formulation of Miehe et al. [19, 20] and Wilson et al. [23] in the way the fracture opening influences the fluid flow.
The pivotal idea behind the phase-field formulation proposed and analyzed herein is to represent the internal discontinuity boundary by an \(\alpha\)-contour of the phase field
with \(0< \alpha < 1\). This boundary separates the domain in a part for which the phase field is larger than the threshold,
to which we refer as the fluid domain, and a part for which the phase is smaller than the threshold,
which we call the solid domain. The unit vector normal to the surface \(\varGamma _\alpha\) is denoted by \(\varvec{n}\) and points into the fluid domain \(\varOmega _{\ominus }\). The procedure to obtain a parametrization of this \(\alpha\)-contour and the corresponding parts of the domain is addressed in Sect. 3.2.
Using the \(\alpha\)-contour the strong form phase-field problem follows as
where \(\varvec{\sigma }(\varvec{\varepsilon },d)\) is the degraded stress tensor (7), and \(\llbracket \varvec{\sigma } \rrbracket = \varvec{\sigma }_{\oplus }-\varvec{\sigma }_{\ominus }\) is the degraded stress jump over the \(\alpha\)-contour. The corresponding weak form problem is
where the function spaces are similar to those in (3), but then equipped with the energy norm corresponding to (12).
2.3 Hybrid fracture formulation
The construction of the internal discontinuity boundary, \(\varGamma _\alpha\), and the fluid and solid domains, \(\varOmega _{\ominus }\) and \(\varOmega _{\oplus }\), provides a setup for a hybrid formulation that mimics the sharp problem in the solid domain, while it mimics the phase-field formulation in the fluid domain. The strong form problem for this hybrid model is written as:
The essential idea of this hybrid model is that the solid domain behaves elastically, i.e., the momentum balance (13a) pertains to the undamaged stress tensor, \(\varvec{\sigma }_e\), while the model behaves as a phase-field model in the fluid domain, which is reflected by the presence of the damaged stress tensor \(\varvec{\sigma }(\varvec{\varepsilon },d)\) in (13b). A Neumann pressure boundary condition is supplied for the solid domain as indicated by the subscript \(\oplus\) in (13e), and the jump in displacement over the interface between the fluid and solid, \(\varGamma _\alpha\), is set to zero. It is important to note that this hybrid model is only coupled in one direction, in the sense that the solution in the solid domain does not depend on the fluid domain, but that the boundary conditions of the fluid domain follow directly from the solution on the solid domain.
The weak solution of the hybrid formulation (13) follows by a two-step procedure. First, the deformation of the solid domain is computed by
where the function space is defined as:
Subsequently, the fluid domain solution is computed by
where the solution to the solid problem (14), \(\varvec{u}_{\oplus }\), is used as a constraint:
2.4 Quantities of interest
In the remainder of this work we will study the performance of the models introduced above for the simulation of pressure-loaded fractures. Although this study is restricted to the approximation behavior for steady fractures, the quantities of interest that we study are selected keeping the extension to propagating fractures in mind. To assess the appropriateness of the models in representing the solid deformation, we consider the energy norm
where the strain tensor, \(\varvec{\varepsilon }(\varvec{u})\), is a function of the displacement field. The associated energy inner product is denoted by \(\left( {\mathbf {u}}, \mathbf {v} \right) _{E(\varOmega {\setminus } \varGamma _c)}\). Moreover we study the \(L^2\)-norm
and \(H^1\)-norm
as quantities of interest. Note that the energy norm and \(H^1\)-norm exclude the discrete crack from the domain, so that the norms of the various models remain bounded. In analogy with the exclusion of the sharp fracture we also consider the \(H^1\)-norm with the fluid domain excluded, i.e., on \(\varOmega _{\oplus }=\varOmega {\setminus } \varOmega _{\ominus }\).
In relation to the envisioned usage of the fluid domain for the modeling of a fluid flow, it is essential to adequately approximate the fracture opening. Herein we consider the integrated fracture surface displacement, i.e., the fracture volume increase, as a quantity of interest:
The thermodynamic driving force field
where \(\psi _e\) is the elastic energy density, is studied to assess the capabilities of the hybrid model for driving fracture propagation. We study the driving force by consideration of the norm
with \(d({\mathbf {u}})\) the solution to the phase-field problem:
The corresponding weak form problem is
with \({\mathcal {V}}^d=H^1(\varOmega )\).
3 Interface parametrization and Galerkin discretization
The remainder of this work focuses on the finite element approximation of the phase-field model and hybrid model, where the sharp crack model will be used as a reference model. In this section we introduce the employed finite element discretization and the parametrization of the pressure-loading surface and the associated fluid and solid sub-domains.
3.1 Galerkin discretization
We consider a mesh \({\mathcal {T}}^h\) that partitions the domain \(\varOmega\), where h is a characteristic mesh parameter. As illustrated in Fig. 3 this mesh does in general not conform to the \(\alpha\)-contour. This mesh is used to construct a computational basis for both the phase field and the displacement field:
Note that the bold font for the displacement field basis functions indicates that these are vector-valued. While the mesh over which the bases are constructed is the same, the discretization spaces can in principle be different. In this work we will consider various B-spline bases, \(\mathrm{span}( \{ N_I \}_{I=1}^n ) = \mathcal {S}_r^k\), where k and r denote the order and regularity of the basis, respectively. The multi-dimensional simulations discussed in Sect. 5 are based on \(C^0\)-continuous linear finite element meshes.
Schematic representation of the employed finite element mesh \({\mathcal {T}}^h\), showing the linear finite element nodes corresponding to: blue circle basis functions with support only in the solid domain \(\varOmega _{\oplus }\); red circle basis functions with support only in the fluid domain \(\varOmega _{\ominus }\); green circle basis functions with support in both the fluid and the solid domain. (Color figure online)
Using the basis for the phase field in combination with the weak form (6) yields the system of equations \(\mathbf {K}^{dd}\mathbf {a}^d=\mathbf {f}^d\) with
where the constraints on the space, i.e. \(d=1\) on \(\varGamma _c\), are either imposed through the space by means of a standard lift approach in the case of a conforming grid, or are resolved through a Lagrange multiplier (field) for non-conforming cases.
The displacement field problem for the phase-field model follows from the system of equations \(\mathbf {K}^{\varvec{u}\varvec{u}}\mathbf {a}^{\varvec{u}}=\mathbf {f}^{\varvec{u}}\), where
for which the Dirichlet data on the external boundary \(\varGamma _D\) is applied through the imposition of constraints on the associated coefficients in the discretization in accordance with a standard lift approach.
The solution of the hybrid model is determined in a two step procedure. In the first step the elasticity problem is solved over the solid domain by \(\mathbf {K}^{\varvec{u}_{\oplus }\varvec{u}_{\oplus }}\mathbf {a}^{\varvec{u}_{\oplus }}=\mathbf {f}^{\varvec{u}_{\oplus }}\), with
in which only the basis functions with support over \(\varOmega _{\oplus }\) are taken into account (the blue and green nodes in Fig. 3). In the second step the degraded elasticity problem is solved over the domain \(\varOmega _{\ominus }\), \(\mathbf {K}^{\varvec{u}_{\ominus }\varvec{u}_{\ominus }}\mathbf {a}^{\varvec{u}_{\ominus }}=\mathbf {f}^{\varvec{u}_{\ominus }}\), with
where all coefficients of basis functions that are also supported in the solid domain (the green nodes in Fig. 3) are constrained to their values as computed in the first step. Effectively this constraining operation lifts the solid solution into the fluid domain, thereby guaranteeing the continuity of the displacement field over the internal boundary \(\varGamma _\alpha\).
3.2 Interface parametrization
In order to evaluate the integrals over the fracture surface boundaries in the weak form problems (12) and (14), a parametrization for the \(\alpha\)-contour is constructed. To obtain this parametrization we employ the bi-sectioning-based segmentation scheme proposed in [24] in the context of the isogeometric finite cell analysis of image-based geometric models, and enrich it with functionality to extract the interface between the segmented regions. The merits of this scheme are that it automatically extracts an interface parametrization from a level set function, i.e. the phase field, for \(n_{\mathrm{dim}}=1,2,3\), while having the capability of resolving the smoothness of the \(\alpha\)-contour in the case of higher-order continuous phase-field discretizations.
For completeness, the bisection-based tessellation scheme proposed in Ref. [24] is schematically shown in Fig. 4. The element-by-element segmentation and interface extraction routine commences with the evaluation of the phase field, \(d(\varvec{x})\), in the vertices associated with a \(\varrho _{\mathrm{max}}\)-times uniform refinement of the element. Subsequently the levels of uniform refinement are traversed, where for each element in that level it is determined whether the interface passes through it. If all vertices of an element exceed the \(\alpha\)-threshold, or if all values are lower than the threshold, the cell is kept as an integration cell. Otherwise a further subdivision of the cell is considered, and the same check is performed on the next refinement level. On the lowest level of refinement, i.e. a \(\varrho _{\mathrm{max}}\)-times uniform element refinement, this recursive bi-sectioning scheme is closed with a tessellation (a triangulation in 2-D and a tetrahedralization in 3-D) based on a point set in which the edge intersections are based on a linear interpolation of the level set function on this lowest level of refinement.
A schematic overview of the tessellation-based interface parametrization technique. The nodal colors match the definitions of Fig. 3. For the coarse mesh shown here there are no nodes whose associated basis function is supported completely inside the fluid domain
On one hand this bisection-based tessellation scheme provides a piecewise parametrization of the regions \(\varOmega _{\oplus }\) and \(\varOmega _{\ominus }\), which enables the construction of integration schemes with controllable precision. On the other hand, the tessellation scheme enables the construction of a piecewise parametrization of the interface between these two domains, \(\varGamma _\alpha\). The interface is constructed by collecting all boundary faces (edges in 2-D) in one of the regions that match a boundary face in the other region. For robustness it is crucial that the boundaries of the two regions are tessellated in a consistent way. As for the volumetric regions, this piecewise parametrization of the interface provides us with the possibility to evaluate integrals over this internal boundary. We note that the cells resulting from this bisection-based tessellation scheme may be distorted, but that this is not a fundamental problem from the perspective of integration.
4 Analysis of a one-dimensional model problem
To gain detailed understanding of the formulations presented in Sect. 2 and the behavior of the discretization schemes introduced in Sect. 3, in this section we study the one-dimensional model problem shown in Fig. 5. The problem consists of a one-dimensional domain of size 2L, \(\varOmega =[-L,L]\), which is clamped on its outer boundaries and with a fully developed fracture centered at the origin, i.e. \(\varGamma _c = \{ 0 \}\). Deformation of the solid in directions other than the x-direction are confined, and the Hookean stress-strain relation \(\sigma _e = E \varepsilon\) is considered. For the results presented below dimensionless values of parameters are chosen. A length of \(L=5\) is used, the modulus of elasticity is taken as \(E=100\), and the pressure is set to \(p=1\).
Under these conditions, the sharp fracture model yields the following solution:
Figure 6a shows the exact solution to the phase-field problem for \(L/l_0= 8\), where the phase field is taken as \(d=\exp {(-|x|/l_0)}\):
where
with \(f(x)=1-\exp {(|x|/l_0)}\). The phase field \(d=\exp {(-|x|/l_0)}\) is evidently only a solution to the strong form problem (5) in the limit that \(l_0/L\) goes to zero. However, for the parameter ranges considered in the remainder the ratio \(l_0/L\) remains small enough to neglect errors associated with the mismatch in the phase-field boundary conditions at the clamped boundaries.
The solution to the hybrid model (13) shown in Fig. 6b follows as:
In the remainder of this section we study the \(\varGamma\)-convergence behavior [1] of the phase-field model and the hybrid model, i.e. the convergence behavior of these models toward the sharp model for decreasing length-scale parameter \(l_0\). Moreover, we study the approximation behavior of the finite element discretizations of the models.
Exact solutions of a the phase-field model and b the hybrid model, both with \(L/l_0=8\) and threshold \(\alpha =0.8\). The sharp solution of the one-dimensional model problem is shown for comparison. Note that for this particular choice of \(l_0\) and \(\alpha\), the difference between the sharp and hybrid solution is hardly visible. A detailed inspection of the differences between these two models follows in Sect. 4.1.2
4.1 \(\varGamma\)-convergence
Prior to studying the finite element approximation behavior we study the dependence of the phase-field solution (32) and hybrid solution (34) on the length-scale parameter \(l_0\). Note that all errors reported below pertain to the difference between the exact solutions presented above and the sharp crack solution (31). The various error norms introduced in Sect. 2.4 have been computed by numerical integration over the domain \(\varOmega {\setminus } \varGamma _c\) on a high-resolution uniform mesh, where one element edge coincides with the sharp crack at \(x=0\). By virtue of the fact that Gauss points are used, this integration procedure automatically removes the singular point \(\varGamma _c=\{ 0 \}\) from the integration domain.
4.1.1 Phase-field model
In Fig. 7 the phase field and displacement field have been plotted for a range of length-scale parameters, \(L/l_0=8,16,32\). This figure conveys that visually the phase-field solution converges to the sharp solution, for both the phase field and the displacement field. The phase-field solution clearly differs from the sharp solution in the vicinity of the pressure loading points at \(\pm x_\alpha\). In the fluid domain, i.e. for \(| x | < x_\alpha\), the solution is constant, with a jump at \(x=0\). In the solid, the slope of the displacement field in the vicinity of the crack is observed to be steeper than that of the sharp solution. The steepness at the loading point is visually independent of the internal length scale. This slope increase is explained by the fact that the internal stress in the solid domain is uniform and equal to the applied pressure load \(-p\), from which the displacement gradient mismatch follows as
Hence, for \(\alpha =0.8\) as used in Fig. 7b, the ratio of the slope of the phase-field model to the slope of the sharp crack model at the pressure boundary is
As a matter of fact, this gradient diverges with \((1-\alpha )^{-2}\) when the damage threshold, \(\alpha\), goes to one.
Figure 8 shows the convergence behavior of the various error measures for a decreasing length-scale parameter \(l_0\). The energy error and the error in the \(H^1\)-norm are both observed to converge with a rate of \(\frac{1}{2}\) as \(l_0\) passes to zero, i.e.,
which follows directly from integration of (35). These rates are dictated by both the gradient mismatch in the fluid domain and in the solid domain, which is confirmed by the observed convergence in the solid domain \(\left\| u_{\mathrm{phase}} - u_{\mathrm{sharp}} \right\| _{H^1(\varOmega {\setminus } \varOmega _{\alpha })} = {\mathcal {O}}(l_0^{\frac{1}{2}})\). Note that since the phase field on the solid domain is bound from above by \(\alpha\), the energy norm over the solid domain is equivalent to this \(H^1\)-norm. The \(\varGamma\)-convergence rate in the \(L^2\)-norm is equal to \(\left\| u_{\mathrm{phase}} - u_{\mathrm{sharp}} \right\| _{L^2(\varOmega {\setminus } \varGamma _{c})} = {\mathcal {O}}(l_0^{\frac{3}{2}})\), which follows from integration of the difference between the phase-field solution (32) and sharp solution (31). The displacement jump converges with \(\left| \llbracket u_{\mathrm{phase}} \rrbracket -\llbracket u_{\mathrm{sharp}} \rrbracket \right| = {\mathcal {O}}(l_0)\), which follows by evaluation of (32) at \(x=\pm x_\alpha\), since in the one-dimensional case the crack opening \(\llbracket u_{\mathrm{phase}} \rrbracket\) is identical to the fracture volume increase (21).
4.1.2 Hybrid model
In Fig. 9 the dependence of the solution of the hybrid model on the length-scale parameter \(l_0\) is shown. By construction, the hybrid model resembles the sharp model in the solid domain, while it resembles the phase field model in the fluid domain. More specifically, the increase in the gradient near the loading points as observed for the phase-field model is not present. The \(\varGamma\)-convergence behavior of the hybrid model reflects this difference in behavior (see Fig. 10). The error in the gradient equals
from which it follows in combination with \(x_\alpha = -l_0\ln {(\alpha )}\) that the energy error and \(H^1\)-error converge with \({\mathcal {O}}( \sqrt{1-\alpha } ) \cdot {\mathcal {O}}(\sqrt{l_0})\) as \(l_0\) goes to zero and \(\alpha\) goes to one. The \(L^2\)-error and jump error converge with order \({\mathcal {O}}( (1-\alpha )^{\frac{3}{2}} )\cdot {\mathcal {O}}(l_0^\frac{3}{2})\) and \({\mathcal {O}}(1-\alpha ) \cdot {\mathcal {O}}(l_0)\), respectively. Note that the \(\varGamma\)-convergence behavior of the \(H^1\)-error over the solid domain is not included in Fig. 10 because it vanishes identically independent of \(l_0\) and \(\alpha\).
4.1.3 Model comparison
The fundamental difference between the phase-field model and hybrid model pertains to the displacement gradients near the loading points. For the phase-field model the displacement gradient is magnified by a factor of \((1-\alpha )^{-2}\) at the exterior of the loading point. This gradient amplification leads to diverging solution behavior in the limit of \(\alpha\) going to one. In contrast, the hybrid model does not suffer from the gradient increase near the loading points, as a consequence of which the solution of the hybrid model converges to the sharp model when the damage threshold goes to one.
The fundamentally different behavior of the two models is reflected in Table 1, which shows that all considered norms of the hybrid model converge with both \(\alpha\) going to one and \(l_0\) going to zero. The phase-field errors for all norms except the \(H^1\)-norm over the solid domain do converge for decreasing \(l_0\) with the same rates as the hybrid model, but they diverge with \(\alpha\) going to one. In Figs. 8 and 10 this difference in behavior is reflected by the error magnitudes, more than by the rates. The energy error and error in the \(H^1\)-norm are observed to be an order of magnitude larger for the phase-field model than for the hybrid model, and a difference of almost two orders of magnitude is observed for the error in the jump.
4.2 h-convergence
In the remainder of this section we study the convergence behavior of the finite element approximations under uniform mesh refinement for both the phase-field model and the hybrid model. All presented simulations pertain to meshes with an odd number of elements, such that both the loading points, and the center of the fracture are not coinciding with element boundaries. Let us note that in terms of observed solution behavior these results do not essentially differ from results with an even number of uniform elements (i.e., with the fracture coinciding with an element boundary).
The error analysis reported below focuses on the non-standard approximation of the displacement field in the phase-field model and hybrid model. The phase-field is in all cases computed using the finite element system (27), supplemented with a Lagrange multiplier constraint to satisfy the \(d(0)=1\) condition. The influence of the error in the phase field on the error in the energy norm and driving force field is observed to be negligible, as the phase field converges at a faster rate under mesh refinement than the displacement field.
4.2.1 Phase-field model
The finite element approximation of the phase-field model is studied by comparing the discrete solution, \(u^h_{\mathrm{phase}}\), to the phase-field solution, \(u_{\mathrm{phase}}\) (32). For all presented results the error associated with the Neumann boundary condition violation of the phase-field solution (32) was found to be insignificant in comparison to the finite element approximation error. Hence, to examine the effect of the order and smoothness of the approximation space, we consider the solution \(u_{\mathrm{phase}}\) as a reference solution for the finite element approximation \(u^h_{\mathrm{phase}}\). The phase-field discretization error is denoted by \(e_{\mathrm{phase}}^h = u_{\mathrm{phase}} -u_{\mathrm{phase}}^h\).
The energy norm The convergence behavior of the error in the energy norm, \(\Vert e_{\mathrm{phase}}^h \Vert _{E(\varOmega {\setminus } \varGamma _c )}\), is shown in Fig. 11a for spline bases of order k and regularity r. The observed rate of convergence of \(\frac{1}{2}\), independent of the order and regularity of the approximation, can be explained by considering the best approximation property of the Galerkin approximation, \(u_{\mathrm{phase}}^h \in {\mathcal {V}}^{u,h} \subset {\mathcal {V}}^{u}\). This property bounds the energy error from above by
for any interpolant \(U_{\mathrm{phase}}^h \in {\mathcal {V}}^{u,h}\). Considering the nodal interpolation
with \(L_i^k(x)\) the \(C^0\)-continuous Lagrange basis functions of order k (with property \(L_i^k(x_j)=\delta _{ij}\)) constructed over the considered uniform grid with spacing h, yields that on those parts of the domain where the solution is smooth:
This standard interpolation rate is impeded by both the kinks in the exact solution at \(x = \pm x_\alpha\) and by the displacement jump at \(x=0\). Using the standard interpolation estimate (41) the error in the best approximation can be bounded as
where \(\pm \bar{x}_\alpha\) are the centers of the elements that contain the kinks at \(\pm x_\alpha\), and where use is made of the continuity of the bilinear operator, i.e. \(\left\| e_{\mathrm{phase}}^h \right\| _{E(\varOmega {\setminus } \varGamma _c )} \le C \left\| e_{\mathrm{phase}}^h \right\| _{H^1(\varOmega {\setminus } \varGamma _c )}\). Note that the continuity of the bilinear operator follows directly from the fact that \(0 \le g(d) \le 1\). For the elements covering the kinks, one can construct a linear interpolant such that \(| u_{\mathrm{phase}}-U_{\mathrm{phase}}^h | = {\mathcal {O}}(h)\) and its derivative \(| u_{\mathrm{phase}}^{\prime}-(U_{\mathrm{phase}}^h)^{\prime} | ={\mathcal {O}}(1)\). Since \(g(d^h)={\mathcal {O}}(1)\) in the vicinity of the kinks, the energy error contribution of the elements covering the kinks converges with
Following the analysis in Ref. [27], from the linear interpolation \(U_{\mathrm{phase}}^h = \frac{\llbracket u_{\mathrm{phase}} \rrbracket }{h} x\) around the crack it follows that
where use is made of the fact that in the limit of h going to zero it holds that \(d^h = 1 - |x|/l_0\). From the integrand in (44) it is observed that the divergence of the gradient \(\llbracket u_{\mathrm{phase}}\rrbracket / h\) under h-refinement is compensated for by the vanishing degradation function \(g(d^h)\approx (x / l_0)^2\). It is important to note that although the energy error converges under mesh refinement, it diverges with the length-scale parameter \(l_0\). Decreasing the length scale (to attain \(\varGamma\)-convergence) therefore increases the energy error in the case that the mesh size is not appropriately refined along with it.
Substitution of of (43) and (44) in the best approximation inequality (42) yields the error estimate
From Fig. 11b it is observed that the convergence rate is independent of the value of the \(\alpha\)-threshold, but that an increase in error is observed as \(\alpha\) increases. This increase in energy is caused by the fact that the error contributions from the steep gradients around the loading point (see Sect. 4.1.1) become larger as the value of \(\alpha\) increases. Since the exact solution (32) diverges as \(\alpha\) goes to one, so does the error in the finite element approximation.
The \(L^2\) -norm and \(H^1\) -norm The convergence plots for the displacement field in the \(L^2(\varOmega )\)-norm, \(H^1(\varOmega )\)-norm and \(H^1(\varOmega _\oplus )\)-norm over the solid domain are shown in Fig. 12 for polynomial degrees \(k=1,2,3\) and regularities \(r=k-1\) and \(r=0\). The discretization independent observed convergence rate of \({\mathcal {O}}(h^{\frac{1}{2}})\) for the \(L^2(\varOmega )\)-norm as observed in Fig. 12a can be deduced from
where \(z_{e^h_{\mathrm{phase}}}\) is the solution to the dual problem:
Since it follows from the Lax-Milgram lemma that the energy norm of the dual solution is bounded from above by
where the positive constant \(C_{\mathrm{sup}}\) corresponds to the largest eigenvalue \(\lambda\) of the generalized eigenvalue problem \(\left( {v}, \tilde{u} \right) _{L^2(\varOmega )}=\lambda \left( {v}, \tilde{u} \right) _{E(\varOmega {\setminus } \varGamma _c)}\,\forall v\in {\mathcal {V}}^u\) (see Fig. 13), the \(L^2\)-norm is bounded from above by
Hence the \(L^2\)-norm converges at least with the same rate as the energy error. For sufficiently smooth functions the bound (49) is generally pessimistic, since no use is made of Galerkin orthogonality in (46). However, the observed rate of convergence for the \(L^2\)-norm in Fig. 12a indicates that for the phase-field problem under consideration the bound (49) is sharp for the convergence rate.
h-convergence behavior of the displacement field error for the phase-field model in a the \(L^2(\varOmega )\)-norm, b The \(H^1(\varOmega )\)-norm, and c the \(H^1(\varOmega ^{\oplus })\)-norm. The solid lines and dashed lines represent Lagrange and B-spline basis functions respectively. The order is represented by k. a \(L^2\)-error. b \(H^1\)-error. c Exterior \(H^1\)-error
Following the same arguments as in [28], the \(H^1\)-norm is expected to diverge with \({\mathcal {O}}(h^{-\frac{1}{2}})\) independent of the order and regularity of the discretization, which is in agreement with the results reported in Fig. 12b. When the fluid domain is excluded, the \(H^1(\varOmega _\oplus )\) norm converges with the same rate as the energy error, i.e. \({\mathcal {O}}(h^\frac{1}{2})\), by virtue of the fact that on the solid domain the energy error and \(H^1\)-norm are equivalent. The minor fluctuations in Fig. 12c are a consequence of the fact that by virtue of the continuity of the bases across the loading contour, the errors associated with the kink in the solution at the loading points behaves irregularly depending on the near coincidence of the loading contour with an element boundary.
Computation of the constant \(C_{\mathrm{sup}}^{h_{\mathrm{ref}}}\) as the maximum eigenvalue of the generalized eigenvalue problem \(\left( {v}^{h_{\mathrm{ref}}}, \tilde{u}^{h_{\mathrm{ref}}} \right) _{L^2(\varOmega )}=\lambda \left( {v}^{h_{\mathrm{ref}}}, \tilde{u}^{h_{\mathrm{ref}}} \right) _{E(\varOmega {\setminus } \varGamma _c)}\,\forall v\in {\mathcal {V}}^{u,{h_{\mathrm{ref}}}}\) on a uniform linear finite element mesh with element size \(h_{\mathrm{ref}}\). a The two eigenfunctions corresponding to the maximum eigenvalue with a multiplicity of two. b Convergence under mesh refinement of \(C_{\mathrm{sup}}^h\) relative to the reference solution \(C_{\mathrm{sup}}^{h_{\mathrm{ref}}}\) with \(h_{\mathrm{ref}} \ll h\). a Eigenfunction. b Relative error
Displacement jump and fracture surface area norm The mesh convergence behavior of the displacement jump is shown in Fig. 14a, where a convergence rate of 1 is observed independent of the order and regularity of the basis. This rate is expected from the fact that the jump can be expressed as
so that the dual problem for the jump is equivalent to the primal problem (6) with pressure \(p=-1\):
As a consequence the dual solution \(z^h\) converges with the same rates as the primal solution. In particular the energy error of the dual solution converges with \(\left\| z - z^h \right\| _{E(\varOmega {\setminus } \varGamma _c)} = {\mathcal {O}}( h^{\frac{1}{2}} )\), corresponding to the derived rate of the primal solution (45). The Babuška–Miller theorem (e.g. [29]) then yields
as \(h\rightarrow 0\).
Figure 14b displays the behavior of the error in the fracture surface area norm (23). This figure shows a rate of convergence of \({\mathcal {O}}(h^{\frac{1}{2}})\). This is explained by the fact that for small element sizes the strain field approaches a function which is equal to \(\llbracket u_{\mathrm{phase}} \rrbracket / h\) for \(|x|<\frac{h}{2}\) and zero everywhere else. The exact solution to (24) with the phase field vanishing at the domain boundaries can in that case be approximated by \(d(u^h_{\mathrm{phase}})=\hat{d} \phi ^h\) with
such that \(\hat{d}\) is equal to the phase field value at the sharp crack boundary. Substitution of \(\phi ^h\) as the single test function in the weak form problem corresponding to (24) then yields
Upon substitution of (53) in (54) and evaluating the integrals, one obtains
from which the coefficient of the approximation \(d(u^h_{\mathrm{phase}})=\hat{d} \phi ^h\) follows as
In the limit of h going to zero, the phase field evidently converges to \(d(u_{\mathrm{phase}})\) with a rate of \({\mathcal {O}}(h)\) in its point value at the sharp crack. It then follows that the corresponding error in the surface area norm converges as
as \(h \rightarrow 0\). One may note that the dominant error is proportional to \(h/l_0\), which indicates the necessity to resolve the length scale \(l_0\) by the mesh to control this error.
4.2.2 Hybrid model
The finite element solution of the hybrid model, \(u^h_{\mathrm{hybrid}}\), is compared with the exact solution, \(u_{\mathrm{hybrid}}\) (34) for the various error norms introduced in Sect. 2.4. The discretization error of the hybrid model is denoted by \(e^h_{\mathrm{hybrid}} = u^h_{\mathrm{hybrid}} - u_{\mathrm{hybrid}}\). As the hybrid solution follows a standard elasticity problem on the solid domain, and a standard phase-field model on the fluid domain, its convergence behavior evidently derives from the properties of these two models. It is noted that the linear displacement field on the solid domain is represented exactly by the computational basis, as a consequence of which various of the error measures vanish. For generalities sake, below we will also report the standard convergence rates of the solid problem.
Energy norm On the solid domain the energy error converges with the standard rate of k, whereas a rate of \(\frac{1}{2}\) was derived above for the fluid domain phase-field model. As a consequence, the rate of convergence of the energy norm is dictated by the phase-field solution, i.e.,
which is corroborated by the results in Fig. 15a. In Fig. 15b the dependence of the error on the threshold \(\alpha\) is shown. Note that by virtue of the fact that the gradient increase near the loading points is not present in the hybrid model, the \(\alpha\)-dependence of the discretization is virtually absent. In particular, the hybrid model does not exhibit the singular behavior of the phase-field model in the limit of \(\alpha \rightarrow 1\).
The \(L^2\) -norm and \(H^1\) -norm In general, the \(H^1\)-norm on the solid domain converges with a rate of k, and the \(L^2\)-norm with a rate of \(k+1\). As derived above for the phase-field model, on the fluid domain the \(H^1\)-norm diverges with a rate of \(\frac{1}{2}\), whereas the \(L^2\)-norm converges with a rate of \(\frac{1}{2}\). As shown in Fig. 16a, b the fluid domain solution behavior dictates the convergence rates of the hybrid model for both the \(L^2\)-norm and \(H^1\)-norm, i.e., \(\Vert e^h_{\mathrm{hybrid}} \Vert _{L^2(\varOmega )}={\mathcal {O}}(h^{\frac{1}{2}})\) and \(\Vert e^h_{\mathrm{hybrid}} \Vert _{H^1(\varOmega {\setminus } \varGamma _c)}={\mathcal {O}}(h^{-\frac{1}{2}})\)
Displacement jump and fracture surface area norm Due to the one-way coupling of the hybrid model, the displacement jump merely depends on the solid solution. Since the energy error for both the primal and the dual problem generally converges with \({\mathcal {O}}(h^k)\), the Babuška–Miller theorem yields
for \(h \rightarrow 0\). By virtue of the fact that the energy error and \(H^1\)-error on the solid domain are identical to zero, so is the error in the displacement jump.
As discussed for the phase-field model, the fracture surface area norm is dictated by the continuous approximation of the jump across the sharp crack. Since this approximation in the hybrid model is identical to that of the phase-field model, the error in the surface area norm behaves very similarly for both models (Fig. 16c).
h-convergence behavior of the displacement field error for the hybrid model in a the \(L^2(\varOmega )\)-norm, b the \(H^1(\varOmega )\)-norm and c the fracture surface area norm. The solid lines and dashed lines represent Lagrange and B-spline basis functions respectively. The order is represented by k. a \(L^2\)-error. b \(H^1\)-error. c Surface area error
4.2.3 Model comparison
In terms of approximation behavior, the errors are generally dictated by the continuous approximation of the jump over the sharp fracture. Since this approximation in the fluid domain is identical for the phase-field model and hybrid model, in terms of rates of convergence there is no different asymptotic behavior for all error norms that involve the fluid domain. This is reflected in Table 2, where identical rates are observed for the energy error, \(H^1\)-error, \(L^2\)-error, and surface area error. A minor difference between the two models is observed from the \(\alpha\)-threshold dependence. While the phase-field model shows error increases (for example in the energy norm) for increasing values of \(\alpha\) due to the approximation of the steep gradients near the loading points, this dependence is absent for the hybrid model.
For error norms that do not involve the fluid domain, the two models do behave fundamentally different. As seen from Table 2 the jump error and \(H^1\)-error over the solid domain converge respectively with rates of 1 and \(\frac{1}{2}\) for the phase-field model. For the hybrid model, these errors are, however, zero up to machine precision by virtue of the fact that on the solid domain the displacement field is linear. In practice in particular the approximation of the displacement jump using the phase-field model is troublesome, as it depends on resolving the gradient increase near the loading points. The hybrid model does not suffer from this complication, as there is no gradient increase on the solid domain.
5 Multi-dimensional simulations
To demonstrate how the results attained above for the one-dimensional case extend to multiple dimensions, in this section we consider a two-dimensional benchmark problem and perform a detailed study of the mesh convergence and \(\varGamma\)-convergence behavior of the phase-field model and hybrid model. Subsequently we demonstrate the applicability of the models and methods in three dimensions.
5.1 A two-dimensional planar crack
We consider the two-dimensional model problem shown in Fig. 17a. The problem consists of a square solid domain \(\varOmega =[-L/2,L/2]\times [-L/2,L/2]\), which is clamped on its outer boundaries and with a fully developed horizontal fracture of length 2c centered at the origin, i.e. \(\varGamma _c = [-c,c] \times \{ 0 \}\). The dimensions and parameters are taken from Ref. [18]. The dimension of the domain is taken as \(L=8\) m and the semi-length of the fracture is \(c=0.2\) m. A plane stress Hookean linear elastic law is used with modulus of elasticity \(E=10\) GPa and Poisson ratio \(\nu =0.3\). The pressure loading is taken as \(p=1\) Mpa.
The sharp solution to this problem closely resembles the classical solution provided by Sneddon [30] by virtue of the fact that since \(L \gg c\) the far field conditions are well represented by the homogeneous Dirichlet conditions on the solid boundary. However, in contrast to the one-dimensional test case studied in the previous section, an analytical reference solution for the phase-field model and hybrid model is not available. To study the \(\varGamma\)-convergence of these models we therefore rely on the finite element approximations of the phase-field model and hybrid model. For that reason we first study the h-convergence behavior in Sect. 5.1.1, before considering the \(\varGamma\)-convergence behavior in Sect. 5.1.2.
5.1.1 Mesh convergence
To study the mesh convergence behavior for the two-dimensional problem we take the length-scale parameter as \(l_0=c/4\). All results presented in this section are based on linear finite elements on locally refined triangular meshes as illustrated in Fig. 17b. In a box with a height and width of \(l_0\times (2c+l_0)\) centered at the sharp crack a uniform mesh with mesh parameter h is created, where h corresponds to the edge lengths of the element edges that coincide with the sharp crack boundary and refinement box. Outside the refinement box the mesh is gradually coarsened as illustrated in Fig. 17b.
The phase-field, \(d^h\), is computed by solving the finite element system (27) where the \(d=1\) constraint is imposed by prescribing the degrees of freedom associated with the nodes on the sharp crack boundary. The approximate phase-field for \(h=l_0/128\) is shown in Fig. 18a. Figure 18b shows part of the corresponding trimmed domain, i.e. the solid domain \(\varOmega _{\oplus }\) and fluid domain \(\varOmega _{\ominus }\), corresponding to a threshold value of \(\alpha =0.8\). Note that Fig. 18b shows the integration sub-cells corresponding to a refinement depth of zero (no bi-sectioning), where the integration scheme discussed in Sect. 3.2 is applied to triangular elements. Due to the fact that the phase field is interpolated linearly, this zero refinement depth yields the exact \(\alpha\)-contour.
Figure 19 displays the Von Mises stress computed using the phase-field model (top) and hybrid model (bottom) for \(h=\frac{l_0}{8},\frac{l_0}{32},\frac{l_0}{64}\). For both models it is observed that along the straight fracture surfaces the Von Mises stress matches the applied pressure load in the solid domain, while it is practically equal to zero in the fluid domain. For the coarsest mesh both models show inaccuracies in the representation of the zero stress behavior in the fluid domain. On this mesh the stress field for the hybrid model is observed to be of better accuracy than that of the phase-field model, in the sense that along the crack surfaces the Von Mises stress shows a better match with the pressure loading. The tip behavior of the two models is distinctly different, in that the tip stresses of the hybrid model are significantly higher than those of the phase-field model for \(l_0=c/4\). This is explained by the fact that for the hybrid model the undamaged material in the solid domain has more load-carrying capacity than the degraded material in the phase-field model. This is evidently consistent with the hybrid model more closely resembling the sharp problem in the solid domain.
Mesh dependence of the Von Mises stress for the phase-field model and hybrid model. The contour plots show a zoom of the domain centered around the fracture. a Phase-field model, \(h=\frac{l_0}{8}\). b Phase-field model, \(h=\frac{l_0}{32}\). c Phase-field model, \(h=\frac{l_0}{64}\). d Hybrid model, \(h=\frac{l_0}{8}\). e Hybrid model, \(h=\frac{l_0}{32}\). f Hybrid model, \(h=\frac{l_0}{64}\)
In Fig. 20a the convergence under mesh refinement of the elastic energy for the phase-field model and hybrid model is shown for a mesh range of \(h=l_0/8,\ldots ,l_0/128\). While the hybrid model gradually converges to a value close to that of the sharp model, \(\varPsi =\pi p^2 c^2 (1-\nu ^2)/E\approx 11.4\) J, the phase-field model converges to a value which is considerably higher. The difference in the asymptotic values as \(h \rightarrow 0\) is explained by the fact that the phase-field model significantly overestimates the fracture opening for this particular choice of the length-scale parameter, \(l_0=c/4\), as is evidenced by the convergence of the fracture volume increase in Fig. 20b. While the volume increase for the hybrid model closely resembles that of the sharp model, \(\varDelta V_c = 2 \pi p c^2 (1-\nu ^2)/E\approx 2.3\cdot 10^{-5}\,\mathrm{m^2}\), the phase-field model significantly over-predicts the volume increase. Note that the close correspondence of the internal elastic energy and the fracture volume increase is due to the internal elastic energy being directly related to the externally applied work. For the hybrid model the discretization error in the elastic energy is dominated by the behavior in the fluid domain, which is corroborated by the observation that the energy over the solid domain is virtually constant.
The significantly higher internal energy and volume increase of the phase-field model is a consequence of the gradient increase near the loading boundary, as was also observed in the one-dimensional problem of the previous section. A similar increase in the strain field near the loading contour is observed in Fig. 21a, which shows the displacement along the vertical center line (\(x=0\)) of the domain. Note that the maximum displacement in Fig. 21a for the phase-field model (resp. Fig. 21c for the hybrid model) is equal to the maximum fracture opening as shown in Fig. 21b (resp. Fig. 21c). It is important to note here that the phase-field model does not only need smaller elements to attain essential mesh independence, but that it also converges to a solution which for this particular choice of \(l_0\) and \(\alpha\) differs significantly from the sharp solution as opposed to the hybrid model. As we will discuss in more detail in the next section, the mesh parameter h and length scale \(l_0\) cannot be selected independently. As a consequence, for decreasing \(l_0\), the mesh insensitivity of the hybrid model compared to the phase-field model is an essential advantage of the former. Another difference in the approximation behavior of the displacement field is seen from the fracture opening evaluated at the loading contour, i.e. Fig. 21b, c. While the hybrid model yields a smooth solution that closely approximates the sharp solution for the considered range of element sizes, the phase-field model shows considerable mesh-dependent fluctuations. These fluctuations are a consequence of the fact that the loading boundary is immersed inside a mesh that continuously interpolates the displacement field, while in the hybrid approach the splitting of the domain effectively makes the loading boundary conforming to the fluid and solid domains.
Mesh convergence behavior of the vertical component of the displacement field for the phase-field model (top) and hybrid model (bottom) along the vertical center line of the domain (left) and along the sharp fracture (right). a Phase-field model, center line displacement. b Phase-field model, fracture opening c Hybrid model, center line displacement. d Hybrid model, fracture opening
In Fig. 22 the dependence of the mesh convergence behavior on the \(\alpha\)-contour is studied. Note that, as discussed above, there is a direct scaling between the elastic energy over the solid domain and the fracture volume increase. As a consequence, for the phase-field model the Figs. 22a, b are scaled versions of one another. Since the elastic energy over the complete domain is considered in Fig. 22c, for the hybrid model the scaling with the fracture volume increase in Fig. 22d is perturbed by the elastic energy in the fluid domain. The most important difference observed between the two models is that the solution of the phase-field model diverges with \(\alpha\) approaching 1, while the hybrid model converges toward the sharp problem solution. This observation is in complete agreement with our analysis of the one-dimensional model problem; see Sect. 4.1.3. In terms of h-convergence behavior the most notable difference between the two models is observed from the fracture opening increase, a quantity of interest that only depends on the solution in the solid domain. The quality of the approximation depends significantly on the mesh size for the phase-field model, since the gradient near the loading boundary must be resolved by the mesh. For this reason, the mesh dependence increases when the \(\alpha\)-threshold approaches 1. In contrast, the volume increase for the hybrid model is virtually independent of the mesh size, since the coarsest meshes considered are already capable of representing the displacement field adequately. These observations are in excellent agreement with our analysis for the one-dimensional model problem; see Sect. 4.2.3.
Mesh convergence behavior of the elastic energy (left) and fracture volume increase (right) for the phase-field model (top) and hybrid model (bottom) for various values of the threshold parameter \(\alpha\). a Phase-field model, elastic energy. b Phase-field model, fracture volume increase. c Hybrid model, elastic energy. d Hybrid model, fracture volume increase
Figure 23 shows the convergence of the fracture surface area norm for both the phase-field model and hybrid model. Note that the result of both models closely resemble the initial phase-field surface area \(S_{\varGamma _c,l_0}\approx 0.4517\) m. The observed minor difference in the results of the hybrid model and the phase-field model is caused by the fact that on the fluid domain both models generate a similar solution for the displacement field, in the sense that both models result in a jump in the displacement field over the fluid domain (see Fig. 21). Accordingly, the computed fracture surface areas are also very similar.
5.1.2 \(\varGamma\)-convergence
In this section we study the dependence of the solution on the length-scale parameter \(l_0\). For all presented results the meshes are defined in accordance with Fig. 17b, with the mesh size parameter equal to \(h=l_0/64\). We consider a range of length-scale parameters \(l_0=c/4,\ldots ,c/16\), for which the associated phase field and fracture surface areas are shown in Fig. 24. Note that the surface area converges to the sharp fracture result of \(2c=0.4\) m from above, with the well-known linear dependence of the error on \(l_0\) [1].
Length scale parameter, \(l_0\), dependence of the phase field. The contour plots show a zoom of the domain centered around the fracture. a \(l_0=\frac{c}{4}\), \(S_{\varGamma _\mathrm{c},l_0}=0.4517\). b \(l_0=\frac{c}{8}\), \(S_{\varGamma _\mathrm{c},l_0}=0.4266\). c \(l_0=\frac{c}{16}\), \(S_{\varGamma _\mathrm{c},l_0}=0.4140\)
Figure 25 shows the Von Mises stress for the phase-field model and hybrid model. Since both models converge to the sharp model, which has a stress singularity at the tip, significant stress concentrations are observed for both models. Evidently, the phase-field model smears out the stresses ahead of the fracture tip, as a consequence of which the stress concentration only becomes visible for a sufficiently small length-scale parameter \(l_0\). The hybrid model on the other hand represents the elastic problem on the solid domain, and hence the stress concentration is already visible for relatively large \(l_0\). The intensity of the stress concentration increases also in this case as the length-scale parameter decreases, but the dependence is much weaker than for the phase-field model. Similar observations are made for the dependence of the Von Mises stress on the threshold parameter, \(\alpha\), as shown in Fig. 26. Most notably, the stress concentration shows a stronger dependence on the \(\alpha\) parameter for the phase-field model than for the hybrid model.
The elastic energy dependence on \(l_0\) for both models is shown in Fig. 27a. For the phase-field model we observe a gradual decrease in the internal energy, which is in one-to-one correspondence with the decrease in fracture volume. This decrease is explained by the fact that the gradient increase near the loading boundary decreases with \(l_0\), as can be seen directly from Fig. 28a. From Fig. 29b it is observed that the fracture opening in the phase-field model gradually converges toward the sharp solution [30]
although differences remain apparent in the tip region even for \(l_0=c/16\). The volume increase and internal energy corresponding to this sharp solution are plotted in Fig. 27 for reference. In contrast to the phase-field model, the energy and the volume increase for the hybrid model are virtually independent of the length-scale parameter. The observed increase in the internal energy over the internal domain can be explained by Eq. (44), which demonstrated that the energy error for an element overlapping the sharp fracture is proportional to the square root of the mesh size, but inversely proportional to the length scale \(l_0\). Since for all simulations presented here the mesh size is taken equal to \(l_0/64\), a decrease in \(l_0\) by a factor of two results in a \(\sqrt{2}\) times increase in the error of the internal elastic energy. This error increase is also present for the phase-field model, but is not visible in that case because other error contributions are dominant. The center line displacement field and fracture opening profile for the hybrid model are shown in Fig. 28c, d. In correspondence with the one-dimensional problem studied in the previous section it is observed that the sharp opening profile is resolved for large values of \(l_0\).
The fracture surface area norm for both the phase-field model and hybrid model is plotted in Fig. 29, from which it is observed that both models converge to the sharp model result of \(2c=0.4\) m. As already observed for the h-convergence behavior, the surface area norm reflects the solution behavior in the fluid domain. Although the fundamental behavior of the displacement field in the fluid domain is the same for the two models, the displacement jump is larger for the phase-field model. As a consequence, also the predicted surface area is larger for the phase-field model.
Length scale parameter, \(l_0\), dependence of the Von Mises stress for the phase-field model and hybrid model. The contour plots show a zoom of the domain centered around the fracture. a Phase-field model, \(l_0=\frac{c}{4}\). b Phase-field model, \(l_0=\frac{c}{8}\). c Phase-field model, \(l_0=\frac{c}{16}\). d Hybrid model, \(l_0=\frac{c}{4}\). e Hybrid model, \(l_0=\frac{c}{8}\). f Hybrid model, \(l_0=\frac{c}{16}\)
Loading contour parameter, \(\alpha\), dependence of the Von Mises stress for the phase-field model and hybrid model. The contour plots show a zoom of the domain centered around the fracture. a Phase-field model, \(\alpha =0.4\). b Phase-field model, \(\alpha =0.6\). c Phase-field model, \(\alpha =0.8\). d Hybrid model, \(\alpha =0.4\). e Hybrid model, \(\alpha =0.6\). f Hybrid model, \(\alpha =0.8\)
\(\varGamma\)-convergence behavior of the vertical component of the displacement field for the phase-field model and hybrid model along the vertical center line of the domain and along the sharp fracture. a Phase-field model, center line displacement. b Phase-field model, fracture opening. c Hybrid model, center line displacement. d Hybrid model, fracture opening
5.2 Three-dimensional interacting penny-shaped cracks
We consider the three-dimensional problem shown in Fig. 30. Two penny-shaped cracks of radius \(R_1=R_2=2\) m are immersed in the domain \(\varOmega =[-L/2,L/2]^3\) with \(L=4\) m. The circular pennies are centered at \(\varvec{c}_1=(0,0,0)\) m and \(\varvec{c}_2=(\frac{1}{2},-\frac{1}{2}\frac{1}{2})\) m, respectively, with the first penny in the xy-plane, and the second penny in a plane that is rotated \(-\,30^\circ\) around the y-axis. The two pennies together constitute the sharp crack boundary \(\varGamma _c\). A Hookean linear elastic law with \(E=10\) GPa and \(\nu =0.3\) is considered, and the internal pressure in the penny-shaped fractures is taken as \(p=1\) Mpa. The displacements on the outer boundaries of the domain are constrained to zero.
We discretize the phase field, \(d^h\), and displacement field, \(\varvec{u}^h\), using a hierarchically refined mesh (see e.g. [31]) with trilinear basis functions. The base mesh consists of \(16 \times 16 \times 16\) elements, and 3 levels of local element refinement are considered in the vicinity of the sharp cracks (see Fig. 31). The locally refined mesh consists of 84134 elements and 299600 scalar basis functions. Since the sharp cracks do not conform to the computational mesh, the phase field cannot be imposed through nodal constraints. Instead we construct the phase field by Eq. (24) with the driving force taken as \({\mathcal {F}}(\varvec{u},d)=2(1-d)\mathcal {H}\), where \(\mathcal {H}=10^5 \times {\mathcal {G}}_c\) on all elements that are intersected by the sharp pennies, and zero everywhere else. The phase field with length-scale parameter \(l_0=0.5\) m is shown in Fig. 31a. The \(\alpha =0.8\) loading contour shown in Fig. 31b is extracted using the algorithm discussed in Sect. 3.2 with a bisectioning depth of 1.
Comparison of the vertical (z-direction) displacement (in meters) of the pressure-loaded penny-shaped crack problem using (left) the phase-field model, and (right) the hybrid model. The deformed configuration, with the displacements magnified by a factor of 500, are depicted in the xz-plane (\(y=0\)) for three choices of the threshold parameter \(\alpha\). a \(\alpha =0.4\). b \(\alpha =0.6\). c \(\alpha =0.8\)
In Fig. 32 the computed vertical (z-direction) displacement field of the problem is shown for both the phase-field model (Fig. 32a) and hybrid model (Fig. 32b). In agreement with the observations made for the one-dimensional model problem and two-dimensional test case discussed above, the displacement jumps in the phase-field model are magnified due to the large displacement gradients in the phase-field model near the loading boundary. For the particular setting considered here, with \(\alpha =0.8\), an amplification of almost a factor of two is observed in comparison to the hybrid model. As for the other examples, the hybrid model closely resembles the sharp fracture problem. Figure 33 compares the two models in the xy-plane for three choices of the threshold parameter \(\alpha\). The increased fracture opening for the phase-field model in comparison to the hybrid model is clearly observed in this figure, where the same color scale is used for both models. In agreement with the results discussed above, the mismatch between the two models decreases as \(\alpha\) decreases. As can be seen from the plotted damage contours, regardless of the selection of \(\alpha\), the discrepancy between the two models vanishes away from the crack, which illustrates that the deviations between the models are essentially localized near the fracture.
6 Conclusions
We have studied the possibility of incorporating the loading of pressurized fractures in phase-field fracture formulations as a non-homogeneous Neumann condition over a phase field contour. Computationally, this approach to modeling the fracture loading is enabled by a bisection-based surface tessellation scheme which was originally developed in the context of immersed finite element simulations. The applicability of this tessellation procedure has been demonstrated for two and three dimensional test cases.
In its simplest form the standard phase-field model for fracture is supplemented with an \(\alpha\)-contour integral to incorporate the pressure loading. The behavior of this model is characterized by the presence of an artificial sharp gradient in the solid displacement field near the loading boundary. This gradient—which results in an overestimation of the fracture opening—is a result of the lowered stiffness near the loading boundary when \(\alpha\) is chosen close to 1. Choosing \(\alpha\) sufficiently close to 1 is required, however, as otherwise the geometric information of the sharp fracture boundaries that is encoded in the phase field is not recovered by the extraction operation. For a fixed value of \(0 \ll \alpha < 1\) the sharp problem solution is recovered when the phase field length-scale parameter, \(l_0\), goes to zero.
In terms of mesh dependence, the h-convergence rates of various norms is impeded by the discretization effects associated with the non-conforming pressure loading and by the approximation of the displacement jump through a continuous displacement field. Evidently, the mesh size h cannot be selected independently of the phase field parameter \(l_0\), since the approximation space should have sufficient resolution in the non-homogeneous part of the phase-field (i.e. near the smeared fractures). For a fixed value of the length-scale parameter, the most notable effect in the phase-field model is the presence of the sharp gradient layer surrounding the fluid domain. This effect does not only result in an \(l_0\)-dependent error of the solid domain deformation, but also creates a significant h-dependent error contribution requiring small elements in the solid domain near the pressure loading boundary.
The shortcomings observed for the phase-field model have led us to the development of a hybrid fracture formulation. The idea of this hybrid formulation is to leverage the computational functionality of the tessellation procedure used for the loading boundary extraction to also provide separate sub-domains for the fluid and the solid. On the solid domain the standard (without phase-field degradation) elasticity problem is then solved, thereby avoiding the occurrence of the gradient increases near the loading boundaries. The solution in the solid is then lifted back into the fluid domain by solving the phase-field problem (in the fluid domain). Effectively the result is a two-step solution procedure that mimics the sharp fracture problem in the solid, and the phase-field model in the fluid domain. More specifically, the hybrid model is capable of accurately representing the sharp problem fracture boundary deformation for length-scale parameters, \(l_0\), and mesh sizes, h, considerably larger than those needed for the phase-field model to obtain the same accuracy.
In terms of the selection of the \(\alpha\)-threshold parameter, the phase-field model and the hybrid model behave differently. For both models, one, in principle, wants to select \(\alpha\) very close to 1, since doing so would yield a loading condition very similar to that of the sharp model. As indicated above, letting the threshold approach 1 in the phase-field model would result in the creation of an artificial, highly compliant, boundary layer, which, practically, leads to e.g. overestimation of the fracture opening. This erroneous behavior is rigorously resolved by the hybrid formulation, as a result of which the compromising conditions to select \(\alpha\) close to 1 as induced by the phase-field model are significantly relaxed. What remains, however, is that the loading zone (i.e., the fluid domain) must be resolved by the computational grid. More specifically, at least a few elements need to be present across the thickness of the fracture to represent the jump in the displacement over the fracture. Hence, bringing \(\alpha\) closer to 1 while keeping the internal length scale constant means that the minimum mesh size must be reduced accordingly. With respect to the selection of \(\alpha\) we finally note that the considerations herein are based on the stationary setting, and that additional selection aspects might need consideration in a propagating fracture setting.
In our future work we aim at extending the hybrid approach to propagating fractures. The conceptual idea of the envisaged extension is to apply the hybrid model in a staggered solution strategy. Given an initial phase field (a preexisting fracture) and loading condition, the domain is segmented (using the \(\alpha\)-threshold) and the hybrid model is used to compute the displacement field, both in the solid domain and in the fluid domain. From the displacement field the thermodynamic driving force is then computed, which serves as the input to the phase-field problem defined over the entire domain. The updated phase-field, along with an update of the loading condition, then again serves as input to the segmentation process and hybrid model. A necessary condition for this staggered approach to work is that the thermodynamic driving force is approximated correctly by the hybrid model. Therefore, we have already studied the behavior of the thermodynamic driving force in this manuscript. The main conclusion of this study is that the hybrid model is capable of mimicking the driving force similar to that of the phase-field model, while significantly improving the accuracy with which the fracture opening is modeled. A detailed investigation of this propagating setting is a topic of further study, which includes a study of how to select the \(\alpha\) parameter, how to treat nucleation from sharply represented initial fractures, and how to deal with non-monotonous pressure loading.
References
Bourdin B, Francfort GA, Marigo J (2008) The variational approach to fracture. J Elast 91:5–148
Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199(45–48):2765–2778
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field fe implementations. Int J Numer Methods Eng 83(10):1273–1311
Karma A (2001) Phase-field formulation for quantitative modeling of alloy solidification. Phys Rev Lett 87(11):115701
de Borst R, Verhoosel CV (2016) Gradient damage vs phase-field approaches for fracture: similarities and differences. Comput Methods Appl Mech Eng 312:78–94
Borden MJ, Verhoosel CV, Scott MA, Hughes TJ, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217–220:77–95
Hofacker M, Miehe C (2012) Continuum phase field modeling of dynamic fracture: variational principles and staggered FE implementation. Int J Fract 178(1–2):113–129
Schlüter A, Willenbücher A, Kuhn C, Müller R (2014) Phase field approximation of dynamic brittle fracture. Comput Mech 54(5):1141–1161
Karma A, Kessler DA, Levine H (2001) Phase-field model of mode III dynamic fracture. Phys Rev Lett 87(4):045501
Hildebrand F, Miehe C (2012) A phase field model for the formation and evolution of martensitic laminate microstructure at finite strains. Philos Mag 92(34):4250–4290
Miehe C, Schänzel LM (2013) Phase field modeling of fracture in rubbery polymers. Part I: finite elasticity coupled with brittle failure. J Mech Phys Solids 65:93–113
Miehe C, Welschinger F, Hofacker M (2010) A phase field model of electromechanical fracture. J Mech Phys Solids 58(10):1716–1740
Abdollahi A, Arias I (2012) Phase-field modeling of crack propagation in piezoelectric and ferroelectric materials with different electromechanical crack conditions. J Mech Phys Solids 60(12):2100–2126
Verhoosel CV, de Borst R (2013) A phase-field model for cohesive fracture. Int J Numer Methods Eng 96(1):43–62
Vignollet J, May S, de Borst R, Verhoosel CV (2014) Phase-field models for brittle and cohesive fracture. Meccanica 49(11):2587–2601
Miehe C, Schänzel LM, Ulmer H (2015) Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput Methods Appl Mech Eng 294:449–485
Miehe C, Hofacker M, Schänzel LM, Aldakheel F (2015) Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic-plastic solids. Comput Methods Appl Mech Eng 294:486–522
Chukwudozie C, Bourdin B, Yoshioka K (eds) (2013) A variational approach to the modeling and numerical simulation of hydraulic fracturing under in-situ stresses. In: Thirty-Eighth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, California
Miehe C, Mauthe S, Teichtmeister S (2015) Minimization principles for the coupled problem of Darcy–Biot-type fluid transport in porous media linked to phase field modeling of fracture. J Mech Phys Solids 82:186–217
Miehe C, Mauthe S (2016) Phase field modeling of fracture in multi-physics problems. Part III. Crack driving forces in hydro-poro-elasticity and hydraulic fracturing of fluid-saturated porous media. Comput Methods Appl Mech Eng 304:619–655
Wheeler MF, Wick T, Wollner W (2014) An augmented-Lagrangian method for the phase-field approach for pressurized fractures. Comput Methods Appl Mech Eng 271:69–85
Mikelić A, Wheeler MF, Wick T (2015) Phase-field modeling of a fluid-driven fracture in a poroelastic medium. Comput Geosci 19(6):1171–1195
Wilson ZA, Landis CM (2016) Phase-field modeling of hydraulic fracture. J Mech Phys Solids 96:264–290
Verhoosel CV, van Zwieten GJ, van Rietbergen B, de Borst R (2015) Image-based goal-oriented adaptive isogeometric analysis with application to the micro-mechanical modeling of trabecular bone. Comput Methods Appl Mech Eng 284:138–164
Chambolle A (2004) An approximation result for special functions with bounded deformation. Journal de Mathématiques Pures et Appliquées 83(7):929–954
Chambolle A (2005) Addendum to “An approximation result for special functions with bounded deformation” [J Math Pures Appl (9) 83 (7) (2004) 929–954]: the N-dimensional case. Journal de Mathématiques Pures et Appliquées 84(1):137–145
Borden MJ, Hughes TJR, Landis CM, Verhoosel CV (2014) A higher-order phase-field model for brittle fracture: formulation and analysis within the isogeometric analysis framework. Comput Methods Appl Mech Eng 273:100–118
van Zwieten GJ, van Brummelen EH, van der Zee KG, Gutiérrez MA, Hanssen RF (2014) Discontinuities without discontinuity: the weakly-enforced slip method. Comput Methods Appl Mech Eng 271:144–166
Babuška I, Miller A (1984) The post-processing approach in the finite element method—part 1: calculation of displacements, stresses and other higher derivatives of the displacements. Int J Numer Methods Eng 20(6):1085–1109
Sneddon I, Lowengrub M (1969) Crack problems in the classical theory of elasticity. The SIAM series in applied mathematics. Wiley, Hoboken
Vuong AV, Giannelli C, Jüttler B, Simeon B (2011) A hierarchical approach to adaptive local refinement in isogeometric analysis. Comput Methods Appl Mech Eng 200(49–52):3554–3567
Acknowledgements
All simulations in this work were performed using the open source software package Nutils (www.nutils.org).
Funding
This work is part of the Industrial Partnership programme (IPP) ’Computational sciences for energy research’ of the NWO Institutes Organisation (NWO-I). This research programme is co-financed by Shell Global Solutions International B.V.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Singh, N., Verhoosel, C.V. & van Brummelen, E.H. Finite element simulation of pressure-loaded phase-field fractures. Meccanica 53, 1513–1545 (2018). https://doi.org/10.1007/s11012-017-0802-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-017-0802-2