Dynamics of masonry walls connected by a vibrating cable in a historic structure

Abstract

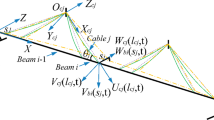
An original parametric model is presented to describe the modal interactions characterizing the linearized free dynamics of a cable–beam system. The structural system is composed by two vertical cantilever beams, connected by a suspended nonlinear cable. A closed form solution is achieved for the linear eigenproblem governing the undamped small-amplitude vibrations. The eigensolution shows a rich scenario of frequency crossing and veering phenomena between global modes, dominated by the beam dynamics, and local modes, dominated by the cable vibrations. Veering phenomena are accompanied by modal hybridization processes. The role played by different parameters is discussed, with focus on the resonance regions. The discussion allows the identification of an updated set of parameters, which offers a satisfying explanation of some unexpected dynamic interactions, observed in the experimental behavior of the masonry walls of the Basilica of Collemaggio, a historic structure heavily damaged by the 2009 L’Aquila earthquake.

Appendix

1.1 Characteristic equation

The frequencies $\beta_{b}$ of the beam eigenfunctions are the infinite positive roots of a characteristic equation, which is given by the singularity condition

$$\det \left( {{\mathbf{B}}(\beta_{b} )} \right) = 0$$

(20)

where the characteristic 8-by-8 matrix ${\mathbf{B}}(\beta_{b} )$ can be expressed

$${\mathbf{B}}(\beta_{b} ) = \left( {\begin{array}{*{20}c} {{\mathbf{B}}_{ 1} (\beta_{b} )} & {{\mathbf{B}}_{ 2} (\beta_{b} )} \\ {{\mathbf{B}}_{ 2} (\beta_{b} )} & {{\mathbf{B}}_{ 1} (\beta_{b} )} \\ \end{array} } \right)$$

(21)

and the 4-by-4 submatrices are

$$\begin{aligned} & {\mathbf{B}}_{ 1} (\beta_{b} ) = \left( {\begin{array}{*{20}c} {C_{c} (\beta_{b} )} & {S_{c} (\beta_{b} )} & {Ch_{c} (\beta_{b} )} & {Sh_{c} (\beta_{b} )} \\ { - B_{s} (\beta_{b} )} & { - B_{c} (\beta_{b} )} & { - Bh_{s} (\beta_{b} )} & { - Bh_{c} (\beta_{b} )} \\ {\beta_{b} } & 0 & {\beta_{b} } & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} } \right) \\ & {\mathbf{B}}_{ 2} (\beta_{b} ) = \hat{e}(\beta_{b} )\,\left( {\begin{array}{*{20}c} {\sin (\beta_{b} )} & {\cos (\beta_{b} )} & {\sinh (\beta_{b} )} & {\cosh (\beta_{b} )} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right) \\ \end{aligned}$$

(22)

The $\beta_{b}$-dependent auxiliary functions read

$$\begin{aligned} & B_{c} (\beta_{b} ) = \beta_{b}^{2} \cos \beta_{b} \\ & B_{s} (\beta_{b} ) = \beta_{b}^{2} \sin \beta_{b} \\ & Bh_{c} (\beta_{b} ) = \beta_{b}^{2} \cosh \beta_{b} \\ & Bh_{s} (\beta_{b} ) = \beta_{b}^{2} \sinh \beta_{b} \\ & C_{c} (\beta_{b} ) = - \chi_{b} \beta_{b}^{3} \cos \beta_{b} - \hat{e}(\beta_{b} )\sin \beta_{b} \\ & S_{c} (\beta_{b} ) = \chi_{b} \beta_{b}^{3} \sin \beta_{b} - \hat{e}(\beta_{b} )\cos \beta_{b} \\ & Ch_{c} (\beta_{b} ) = \chi_{b} \beta_{b}^{3} \cosh \beta_{b} - \hat{e}(\beta_{b} )\sinh \beta_{b} \\ & Sh_{c} (\beta_{b} ) = \chi_{b} \beta_{b}^{3} \sinh \beta_{b} - \hat{e}(\beta_{b} )\cosh \beta_{b} \\ \end{aligned}$$

(23)

while the implicit $\beta_{b}$—dependence of the function

$$\hat{e}(\beta_{b} ) = \frac{\alpha }{{\left\{ {1 + \left[ {\frac{{\lambda^{2} }}{{\beta_{c}^{2} }}\left( {1 - \frac{2}{{\beta_{c} }}\tan\frac{{\beta_{c} }}{2}} \right)} \right]} \right\}}}$$

(24)

follows from the relation (10).

1.2 Eigenfunctions

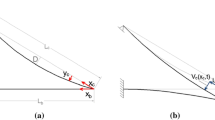
The beam and cable eigenfunctions are

$$\begin{aligned} \varphi_{b1} (x_{b} ) = & C_{1} \sin (\beta_{b} x_{b} ) + C_{2} \cos (\beta_{b} x_{b} ) \\ & + C_{3} \sinh (\beta_{b} x_{b} ) + C_{4} \cosh (\beta_{b} x_{b} ) \\ \varphi_{b2} (x_{b} ) = & C_{5} \sin (\beta_{b} x_{b} ) + C_{6} \cos (\beta_{b} x_{b} ) \\ & + C_{7} \sinh (\beta_{b} x_{b} ) + C_{8} \cosh (\beta_{b} x_{b} ) \\ \varphi_{c} (x_{c} ) = & C_{9} \sin (\beta_{c} x_{c} ) + C_{10} \sin (\beta_{c} x_{c} ) + \frac{{8\mu \,\nu \,\tilde{e}}}{{\beta_{c}^{2} }} \\ \end{aligned}$$

(25)

If $C_{1}$ is intended as indeterminate modal amplitude, the other coefficients read

$$\begin{aligned} & C_{2} = - C_{1} \frac{{\sin \beta_{b} + \sinh \beta_{b} }}{{\cos \beta_{b} + \cosh \beta_{b} }} \\ & C_{3} = - C_{1} \\ & C_{4} = - C_{1} \frac{{\sin \beta_{b} - \sinh \beta_{b} }}{{\cos \beta_{b} + \cosh \beta_{b} }} \\ & C_{5} = - 2C_{1} \hat{e}(\beta_{b} )M_{c} (\beta_{b} )P_{d} (\beta_{b} )D(\beta_{b} ) \\ & C_{6} = 2C_{1} \hat{e}(\beta_{b} )M_{c} (\beta_{b} )P_{d} (\beta_{b} )D(\beta_{b} ) \\ & C_{7} = 2C_{1} \hat{e}(\beta_{b} )M_{s} (\beta_{b} )P_{d} (\beta_{b} )D(\beta_{b} ) \\ & C_{8} = - 2C_{1} \hat{e}(\beta_{b} )M_{s} (\beta_{b} )P_{d} (\beta_{b} )D(\beta_{b} ) \\ & C_{9} = \frac{{8\mu {\kern 1pt} \nu {\kern 1pt} \tilde{e}}}{{\beta_{c}^{2} }}\frac{{(\cos \beta_{c} - 1)}}{{\sin \beta_{c} }} \\ & C_{10} = - \frac{{8\mu {\kern 1pt} \nu {\kern 1pt} \tilde{e}}}{{\beta_{c}^{2} }} \\ \end{aligned}$$

(26)

where the following auxiliary functions have been introduced

$$\begin{aligned} & D(\beta_{b} ) = \left( {M_{c} \left( {\beta_{b} } \right)\left[ {\chi \beta_{b}^{3} Q\left( {\beta_{b} } \right) - 2\hat{e}\left( {\beta_{b} } \right)P_{d}( {\beta_{b} }} \right]} \right)^{ - 1} \\ &P_{d} \left( {\beta_{b} } \right) = \cos \beta_{b} \sinh \beta_{b} - \cosh \beta_{b} \sin \beta_{b} \\ &Q({\beta_{b} }) = \cos \left( {\beta_{b}^{2} } \right) + 2\cos \left( {\beta_{b} } \right)\cosh \left( {\beta_{b} } \right) + \\ &\quad + \cosh \left( {\beta_{b}^{2} } \right) + \sin \left( {\beta_{b}^{2} } \right) - \sinh \left( {\beta_{b}^{2} } \right) \\ & M_{c} ({\beta_{b} }) = \cos \beta_{b} + \cosh \beta_{b} \\ & M_{s} ({\beta_{b} }) = \sin \beta_{b} + \sinh \beta_{b} \\ \end{aligned}$$

(27)