Screw dislocation near a piezoelectric oblique edge crack

Abstract

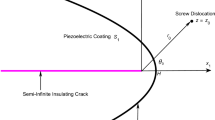
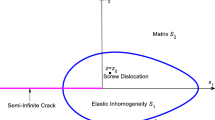
The interaction between a screw dislocation and an oblique edge crack in a semi-infinite piezoelectric medium under remote anti-plane mechanical and in-plane electrical loadings is studied in this article. The screw dislocation suffers a finite discontinuity in the displacement and electric potential across the slip plane. The dislocation also has a line force and a line charge along its core. In the framework of linear piezoelectricity theory, the analytical solutions are derived from the complex variable and Schwarz–Christoffel transformation. Furthermore, the electric field, stress field, generalized stress intensity factor, image force and crack extension force are formulated exactly. Numerical calculations are then given graphically for studying the effects of crack length, crack angle and load position on these electric mechanical parameters. Besides, the dislocation solutions proposed here can be served as Green’s functions for the analyses of corresponding piezoelectric cracking or distributed loading problems.

Appendix

• (a) The derivation of (38).

From (14)

$$\begin{aligned} m(\zeta ) & = \frac{a}{{\alpha^{1 - (\omega /\pi )} }}(\zeta + \alpha )^{1 - (\omega /\pi )} (\zeta - 1)^{(\omega /\pi )} \\ & = \frac{a}{{\alpha^{1 - (\omega /\pi )} }}( - 1)^{{^{(\omega /\pi )} }} (\zeta + \alpha )^{1 - (\omega /\pi )} (1 - \zeta )^{(\omega /\pi )} \\ & = \frac{{ae^{i\omega } }}{{\alpha^{1 - (\omega /\pi )} }}(\zeta + \alpha )^{1 - (\omega /\pi )} (1 - \zeta )^{(\omega /\pi )} \\ \end{aligned}$$

(51)

$$\begin{aligned} m^{\prime } (\zeta ) & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(1 - \omega /\pi )(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} } \right. \\ & = \left. { - (\omega /\pi )(\zeta + \alpha )^{{(1 - \omega /\pi )}} (1 - \zeta )^{{(\omega /\pi - 1)}} } \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} - \omega /\pi } \right. \\ & = \left. {\left[ {(\zeta + \alpha )^{{ - \omega /\pi }} (1 - \zeta )^{{\omega /\pi }} + (\zeta + \alpha )^{{(1 - \omega /\pi )}} (1 - \zeta )^{{(\omega /\pi - 1)}} } \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} - \omega /\pi } \right. \\ & = \left. {\left[ {(\zeta + \alpha )^{{ - \omega /\pi }} (1 - \zeta )^{{\omega /\pi }} [1 + (\zeta + \alpha )(1 - \zeta )^{{ - 1}} ]} \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} } \right. \\ & = \left. {\left[ {1 - \omega /\pi [1 + (\zeta + \alpha )(1 - \zeta )^{{ - 1}} ]} \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} } \right. \\ & = \left. {\left[ {1 - \omega /\pi [1 + (\zeta + \pi /\omega - 1)(1 - \zeta )^{{ - 1}} ]} \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} } \right. \\ & = \left. {\left[ {1 - \omega /\pi [1 + (\zeta - 1)(1 - \zeta )^{{ - 1}} + \pi /\omega (1 - \zeta )^{{ - 1}} ]} \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} \left[ {1 - (1 - \zeta )^{{ - 1}} } \right]} \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {(\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi )}} \left[ {\frac{{ - \zeta }}{{(1 - \zeta )}}} \right]} \right\} \\ \end{aligned}$$

(52)

$$\mathop {\lim }\limits_{\zeta \to 0} m^{\prime } (\zeta ) = - \frac{a}{\alpha }e^{i\omega } \zeta$$

• (b) The derivation of (39)

$$\sqrt {r - a} = \left( {\frac{m(\zeta )}{{e^{i\omega } }} - a} \right)^{\frac{1}{2}}$$

$$\mathop {\lim }\limits_{r \to a} \sqrt {r - a} = \mathop {\lim }\limits_{\zeta \to 0} \left( {\frac{m(\zeta )}{{e^{i\omega } }} - a} \right)^{\frac{1}{2}}$$

(53)

$$\mathop {\lim }\limits_{\zeta \;\to\; 0} m(\zeta )\, \doteq\, m^{\prime } (0) + m^{\prime } (0)\zeta + \frac{{m^{\prime \prime } (0)}}{2}\zeta^{2} + \cdots$$

(54)

From (51),

$$m(0) = ae^{i\omega }$$

(55)

From (52),

$$m^{\prime } (0) = 0$$

(56)

$$\begin{aligned} m^{{\prime \prime }} (\zeta ) & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {\begin{array}{*{20}l} {(\omega /\pi )(\omega /\pi - 1)\left[ {(\zeta + \alpha )^{{ - (\omega /\pi ) - 1}} (1 - \zeta )^{{(\omega /\pi )}} } \right.} \hfill \\ { + (\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi - 1)}} + (\zeta + \alpha )^{{1 - (\omega /\pi )}} } \hfill \\ {\left. {(1 - \zeta )^{{(\omega /\pi - 2)}} + (\zeta + \alpha )^{{ - (\omega /\pi )}} (1 - \zeta )^{{(\omega /\pi - 1)}} } \right]} \hfill \\ \end{array} } \right\} \\ & = \frac{{ae^{{i\omega }} }}{{\alpha ^{{1 - (\omega /\pi )}} }}\left\{ {\frac{{ - \alpha }}{{(1 + \alpha )^{2} }}\left[ {\alpha ^{{1 - (\omega /\pi )}} \left( {\alpha ^{{ - 2}} + \alpha ^{{ - 1}} + \alpha ^{{ - 1}} + 1} \right)} \right]} \right\} \\ \end{aligned}$$

(57)

From (57),

$$m^{\prime \prime } (0) = - \frac{a}{\alpha }e^{i\omega }$$

(58)

substituting (55), (56) and (58) into (54) and (53), get

$$\mathop {\lim }\limits_{r \to a} \sqrt {r - a} = \mathop {\lim }\limits_{\zeta \to 0} \left( {\frac{m(\zeta )}{{e^{i\omega } }} - a} \right)^{\frac{1}{2}} = - i\sqrt {\frac{a}{2\alpha }} \zeta$$