Abstract
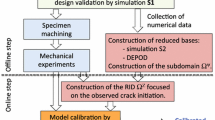
Finite element (FE) elasto-plastic or elasto-viscoplastic simulations of complex components can still be prohibitive for lifetime predictions. There is a need for fast estimation methods of plasticity in a given region of interest, where a crack could be initiated. Some rules are already available for fast predictions of elasto-plastic stress and strain, by using elastic simulations. Furthermore, as shown by the Herbland’s model, inclusion theory can be incorporated in simplified rules to improve their accuracy. Recent advances in model reduction methods for nonlinear mechanical models give access to fast elasto-plastic or elasto-viscoplastic predictions having both accuracy and computational complexity in between usual FE predictions and these simplified rules. Hyper-reduction performs quite well in the simplification of elasto-plastic or elasto-viscoplastic models. Similarly to Herbland’s model, we show in this paper a first attempt to improve hyper-reduced models by the recourse to a virtual inclusion placed in the region of interest. In the proposed numerical example, a finite element model involving 5000 degrees of freedom is reduced to 12 variables. The mesh is also reduced to 550 elements over a total of 900 elements for the original mesh. The approximation error on the predicted plastic strains and stresses is lower than 3 % and the computational time is reduced up to a factor 5.




Similar content being viewed by others
References
Alexandrov N, Dennis J, Lewis R, Torczon V (1998) A trust-region framework for managing the use of approximation models in optimization. Struct Optim 15:16–23
Arian E, Fahl M, Sachs EW (2000) Trust-region proper orthogonal decomposition for flow control. Technical report 25 ICASE, Ohio University
Astrid P (2004) Reduction of process simulation models: a proper orthogonal decomposition approach. PhD thesis, Technische Universiteit Eindhoven, ISBN 90-386-1653-8
Barrault M, Maday Y, Nguyen NC, Patera AT (2004) An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. C R Acad Sci Paris Ser I 339:667–672
Bergmann M, Cordier L (2008) Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced-order models. J Comput Phys 227:7813–7840
Besson J, Cailletaud G, Chaboche J-L, Forest S (2001) Mécanique non-lineaire des matériaux. Hermes, Paris
Cailletaud G, Chaboche JL (1982) Lifetime predictions in 304 stainless steel by damage approach. In: ASME-PVP conference, Orlando, Florida
Carlberg K, Bou-Mosleh C, Farhat C (2011) Efficient non-linear model reduction via a least-squares Petrov-Galerkin projection and compressive tensor approximations. Int J Numer Methods Eng 86:155–181
Carlberg K, Cortial J, Amsallem D, Zahr M, Farhat C (2011) The GNAT nonlinear model reduction method and its application to fluid dynamics problems. 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii, June 27–30, pp 2011–3112
Chouman M, Gaubert A, Chaboche J, Kanout P, Cailletaud G, Quilici S (2014) Elastic-viscoplastic notch correction methods. Int J Solids Struct 51(18):3025–3041. doi:10.1016/j.ijsolstr.2014.04.017
Dvorak GJ (1992) transformation field analysis of inelastic composite-materials. Proc R Soc Lond Ser A Math Phys Eng Sci 437(1900):311–327
Everson R, Sirovich L (1995) Karhunen-Loève procedure for gappy data. J Opt Soc Am A 12:1657–1664
Galbally D, Fidkowski K, Willcox K, Ghattas O (2010) Non-linear model reduction for uncertainty quantification in large-scale inverse problems. Int J Numer Methods Eng 81:1581–1608
Lampoh K, Charpentier I, Daya EM (2011) A generic approach for the solution of nonlinear residual equations. part III: sensitivity computations. Comput Methods Appl Mech Eng 200:2983–2990
Lorenz EN (1956) Empirical orthogonal functions and statistical weather prediction. Scientific report 1, MIT Departement of Meteorology, Statistical Forecasting Project
Lumley J (1967) The structure of inhomogeneous turbulence. Atmospheric turbulence and wave propagation. Nauka, Moscow, pp 166–178
Michel J, Suquet P (2003) Nonuniform transformation field analysis. Int J Solids Struct 40:6937–6955
Neuber H (1961) Theory of stress concentration for shear-strained prismatic bodies with arbitrary non-linear stressstrain law. J Appl Mech 28:544–551
Ryckelynck D (2005) A priori hypereduction method: an adaptive approach. Int J Comput Phys 202:346–366
Ryckelynck D (2009) Hyper reduction of mechanical models involving internal variables. Int J Numer Methods Eng 77(1):75–89
Ryckelynck D, Gallimard L, Jules S (2015) Estimation of the validity domain of hyper-reduction approximations in generalized standard elastoviscoplasticity. Adv Model Simul Eng Sci 2(1):6. doi:10.1186/s40323-015-0027-7
Ryckelynck D, Missoum Benziane D (2010) Multi-level a priori hyper reduction of mechanical models involving internal variables. Comput Methods Appl Mech Eng 199:1134–1142
Schmidt A, Potschka A, Koerkel S, Bock HG (2013) Derivative-extended pod reduced-order modeling for parameter estimation. SIAM J Sci Comput 35:A2696–A2717
Sirovich L (1987) Turbulence and the dynamics of coherent structures part I : coherent structures. Q Appl Math 65(3):561–571
Sirovich L (1987) Turbulence and the dynamics of coherent structures part III : dynamics and scaling. Q Appl Math 65(3):583–590
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ryckelynck, D., Lampoh, K. & Quilicy, S. Hyper-reduced predictions for lifetime assessment of elasto-plastic structures. Meccanica 51, 309–317 (2016). https://doi.org/10.1007/s11012-015-0244-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-015-0244-7