Skip to main content
SpringerLink
Log in

Geometrically nonlinear dynamic analysis of functionally graded thick hollow cylinders using total Lagrangian MLPG method

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

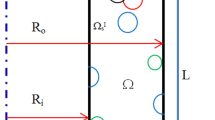
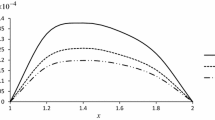
In this article, geometrically nonlinear transient analysis based on the meshless local Petrov–Galerkin method (MLPG) is presented for functionally graded material thick hollow cylinders with infinite length subjected to a mechanical shock loading. The cylinder is assumed to be axisymmetric and in plane strain conditions. The mechanical properties of functionally graded cylinder are assumed to vary across the thickness. In MLPG analysis, the total Lagrangian formulation, radial base function, and Heaviside test function are used for approximation of displacement field in the weak form of the equation of motion. The system nonlinear equations are solved by Newmark finite difference and Newton–Raphson iteration methods. The time history of the radial displacement and stress for various values of the power law exponents, radii and thicknesses are investigated. The effects of different loading types and also the duration of loading on the dynamic behaviors of displacement and stress fields are obtained and discussed in details. Moreover, the obtained results from nonlinear analysis are compared with those obtained from linear analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

References

  1. Suresh S, Mortensen A (1998) Fundamentals of functionally graded materials. IOM Communications Ltd, London

    Google Scholar 

  2. Birman V, Byrd LW (2007) Modeling and analysis of functionally graded materials and structures. Appl Mech Rev 60:195–216

    Article  ADS  Google Scholar 

  3. Alwar RS, Reddy BS (1979) Large deflection static and dynamic analysis of isotropic and orthotropic annular plates. Int J Non-Linear Mech 14:347–359

    Article  MATH  Google Scholar 

  4. Reddy JN, Huang CL (1981) Nonlinear axisymmetric bending of annular plates with varying thickness. Int J Solids Struct 17:811–825

    Article  MATH  Google Scholar 

  5. Dumir PC (1988) Large deflection axisymmetric analysis of orthotropic annular plates on elastic foundations. Int J Solids Struct 24:777–787

    Article  Google Scholar 

  6. Srinivasan RS, Ramachandra LS (1989) Large deflection analysis of bimodulus annular and circular plates using finite elements. Comput Struct 31:681–691

    Article  MATH  Google Scholar 

  7. Shiue F-C (1989) Geometrically nonlinear analysis for an elastic body by the boundary element method. Retrospective theses and dissertations, Iowa State University

  8. Shiue F-C (1991) Application of sub-element technique for improving the interior displacement and stress calculations by using the boundary element method. In: Brebbia CA et al (eds) Bound elem XIII. Springer, Netherlands, pp 1005–1013

    Chapter  Google Scholar 

  9. Woo J, Meguid SA (2001) Nonlinear analysis of functionally graded plates and shallow shells. Int J Solids Struct 38:7409–7421

    Article  MATH  Google Scholar 

  10. Reddy JN, Arciniega RA (2006) Nonlinear analysis of composite and FGM shells using tensor-based shell finite elements. In: Motasoares CA et al (eds) III European conference on computational mechanics. Springer, Netherlands, pp 31–32

    Chapter  Google Scholar 

  11. Arciniega RA, Reddy JN (2007) Large deformation analysis of functionally graded shells. Int J Solids Struct 44:2036–2052

    Article  MATH  Google Scholar 

  12. Owatsiriwong A, Park KH (2008) A BEM formulation for transient dynamic elastoplastic analysis via particular integrals. Int J Solids Struct 45:2561–2582

    Article  MATH  Google Scholar 

  13. Zhao X, Liew KM (2009) Geometrically nonlinear analysis of functionally graded shells. Int J Mech Sci 51:131–144

    Article  MATH  Google Scholar 

  14. Sepahi O, Forouzan MR, Malekzadeh P (2010) Large deflection analysis of thermo-mechanical loaded annular FGM plates on nonlinear elastic foundation via DQM. Compos Struct 92:2369–2378

    Article  Google Scholar 

  15. Ke L-L, Yang J, Kitipornchai S (2010) An analytical study on the nonlinear vibration of functionally graded beams. Meccanica 45:743–752

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhang W, Hao Y, Guo X (2012) Complicated nonlinear responses of a simply supported FGM rectangular plate under combined parametric and external excitations. Meccanica 47:985–1014

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhang W, Hao YX, Yang J (2012) Nonlinear dynamics of FGM circular cylindrical shell with clamped–clamped edges. Sci Technol 94:1075–1086

    Google Scholar 

  18. Akinola AP, Fadodun OO, Olokuntoye BA (2012) Large deformation of transversely isotropic elastic thin circular disk in rotation. Int J Basic Appl Sci 12:22–26

    Google Scholar 

  19. Upadhyay AK, Shukla KK (2013) Geometrically nonlinear static and dynamic analysis of functionally graded skew plates. Commun Nonlinear Sci Numer Simul 18:2252–2279

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Arefi M (2013) Nonlinear thermoelastic analysis of thick-walled functionally graded piezoelectric cylinder. Acta Mech 224:2771–2783

    Article  MathSciNet  MATH  Google Scholar 

  21. Dong L, Hao Y, Wang J, Yang L (2013) Nonlinear vibration of functionally graded material cylindrical shell based on Reddy’s third-order plates and shells theory. Adv Mater Res 625:18–24

    Article  Google Scholar 

  22. Panda SK, Mahapatra TR (2014) Nonlinear finite element analysis of laminated composite spherical shell vibration under uniform thermal loading. Meccanica 49:191–213

    Article  MathSciNet  MATH  Google Scholar 

  23. Zhang A, Ming F, Cao X (2014) Total Lagrangian particle method for the large-deformation analyses of solids and curved shells. Acta Mech 225:253–275

    Article  MathSciNet  MATH  Google Scholar 

  24. Borboni A, De Santis D (2014) Large deflection of a non-linear, elastic, asymmetric Ludwick cantilever beam subjected to horizontal force, vertical force and bending torque at the free end. Meccanica 49:1327–1336

    MathSciNet  MATH  Google Scholar 

  25. Enshaeian A, Rofooei FR (2014) Geometrically nonlinear rectangular simply supported plates subjected to a moving mass. Acta Mech 608:595–608

    Article  MathSciNet  Google Scholar 

  26. Shegokar NL, Lal A (2014) Stochastic finite element nonlinear free vibration analysis of piezoelectric functionally graded materials beam subjected to thermo-piezoelectric loadings with material uncertainties. Meccanica 49:1039–1068

    Article  MathSciNet  MATH  Google Scholar 

  27. Atlut SN, Zhu TL (1998) A new MLPG approach to nonlinear problems in computer modeling and simulation. Comput Model Simul Eng 3:187–196

    Google Scholar 

  28. Sladek J, Stanak P, Han Z et al (2013) Applications of the MLPG method in engineering & sciences : a review. Tech Sci Press 92:423–475

    Google Scholar 

  29. Xiong YB, Long SY, Hu DA, Li GY (2006) An application of the local petrov-galerkin method in solving geometrically nonlinear problems. In: Liu GR, Tan VBC, Han X (eds) Computational methods. Springer, Netherlands, pp 1509–1514

    Chapter  Google Scholar 

  30. Xiong YB, Long SY, Liu KY, Li GY (2006) A meshless local Petrov-Galerkin method for elasto-plastic problems. In: Liu GR, Tan VBC, Han X (eds) Computational methods. Springer, Netherlands, pp 1477–1478

    Chapter  Google Scholar 

  31. Zhang X, Yao Z, Zhang Z (2006) Application of MLPG in large deformation analysis. Acta Mech Sin 22:331–340

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Soares JD (2010) A time-domain meshless local Petrov–Galerkin formulation for the dynamic analysis of nonlinear porous media. Tech Sci Press 66:227–248

    MathSciNet  MATH  Google Scholar 

  33. Soares JD, Sladek J, Sladek V (2009) Dynamic analysis by meshless local Petrov–Galerkin formulations considering a time-marching scheme based on implicit Green’s functions. Comput Model Eng Sci 50:115–140

    MathSciNet  MATH  Google Scholar 

  34. Soares JD, Sladek J, Sladek V (2010) Non-linear dynamic analyses by meshless local Petrov–Galerkin formulations. Int J Numer Eng 82:1687–1699

    MathSciNet  Google Scholar 

  35. Wang D, Sun YUE (2011) A Galerkin meshfree method with stabilized conforming nodal integration for geometrically nonlinear analysis of shear deformable plates. Int J Comput Methods 8:685–703

    Article  MathSciNet  MATH  Google Scholar 

  36. Moosavi MR, Khelil A (2015) Isogeometric meshless finite volume method in nonlinear elasticity. Acta Mech 226:123–135

    Article  MathSciNet  MATH  Google Scholar 

  37. Ghadiri Rad MH, Shahabian F, Hosseini SM (2014) A meshless local Petrov–Galerkin method for nonlinear dynamic analyses of hyper-elastic FG thick hollow cylinder with Rayleigh damping. Acta Mech. doi:10.1007/s00707-014-1266-2

    Google Scholar 

  38. Ghadiri Rad MH, Shahabian F, Hosseini SM (2015) Geometrically nonlinear elastodynamic analysis of hyper-elastic neo-Hooken FG cylinder subjected to shock loading using MLPG method. Eng Anal Bound Elem 50:83–96

    Article  MathSciNet  Google Scholar 

  39. Liu GR, Gu YT (2005) An introduction to meshfree methods and their programming. Springer, New York

    Google Scholar 

  40. Moussavinezhad SM, Shahabian F, Hosseini SM (2013) Two-dimensional elastic wave propagation analysis in finite length FG thick hollow cylinders with 2D nonlinear grading patterns using MLPG method. Tech Sci Press 1:1–27

    Google Scholar 

  41. Santos H, Soares CMM, Soares CAM, Reddy JN (2005) A semi-analytical finite element model for the analysis of laminated 3D axisymmetric shells Bending, free vibration and buckling. Compos Struct 71:273–281

    Article  Google Scholar 

  42. Zhu Y, Luo XY, Ogden RW (2010) Nonlinear axisymmetric deformations of an elastic tube under external pressure. Eur J Mech/A Solids 29:216–229

    Article  MathSciNet  Google Scholar 

  43. Bathet KJ, Bolourchit S (1979) Large displacement analysis of three-dimensional beam structures. Int J Numer Eng 14:961–986

    Article  Google Scholar 

  44. Reddy JN (2004) An introduction to nonlinear finite element analysis. Oxford University Press, New York

    Book  MATH  Google Scholar 

  45. Bathe KJ, Ramm E, Wilson EL (1975) Finite element formulations for large deformation dynamic analysis. Int J Numer Methods Eng 9:353–386

    Article  MATH  Google Scholar 

  46. Hosseini SM, Akhlaghi M, Shakeri M (2007) Dynamic response and radial wave propagation velocity in thick hollow cylinder made of functionally graded materials. Eng Comput 24:288–303

    Article  MATH  Google Scholar 

  47. Shariyat M, Nikkhah M, Kazemi R (2011) Exact and numerical elastodynamic solutions for thick-walled functionally graded cylinders subjected to pressure shocks. Int J Press Vessel Pip 88:75–87

    Article  Google Scholar 

  48. Moradi-dastjerdi R, Foroutan M, Pourasghar A (2013) Dynamic analysis of functionally graded nanocomposite cylinders reinforced by carbon nanotube by a mesh-free method. J Mater Des 44:256–266

    Article  Google Scholar 

  49. Upadhyay AK, Pandey R, Shukla KK (2011) Nonlinear dynamic response of laminated composite plates subjected to pulse loading. Commun Nonlinear Sci Numer Simul 16:4530–4544

    Article  ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lean Production Engineering Research Center, Mechanical Engineering Department, Ferdowsi University of Mashhad, PO Box 91775-1111, Mashhad, Iran

    Seyed Yaghoub Sajadi & Mohammad Hossein Abolbashari

  2. Industrial Engineering Department, Faculty of Engineering, Ferdowsi University of Mashhad, PO Box 91775-1111, Mashhad, Iran

    Seyed Mahmoud Hosseini

Authors
  1. Seyed Yaghoub Sajadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad Hossein Abolbashari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Seyed Mahmoud Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammad Hossein Abolbashari.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sajadi, S.Y., Abolbashari, M.H. & Hosseini, S.M. Geometrically nonlinear dynamic analysis of functionally graded thick hollow cylinders using total Lagrangian MLPG method. Meccanica 51, 655–672 (2016). https://doi.org/10.1007/s11012-015-0228-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0228-7

Keywords

Search

Navigation