Size-dependent axial buckling analysis of functionally graded circular cylindrical microshells based on the modified strain gradient elasticity theory

Abstract

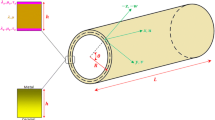
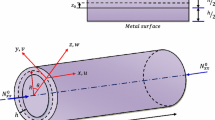
In this paper, a size-dependent first-order shear deformable shell model is developed based upon the modified strain gradient theory (MSGT) for the axial buckling analysis of functionally graded (FG) circular cylindrical microshells. It is assumed that the material properties of FG materials, which obey a simple power-law distribution, vary through the thickness direction. The principle of virtual work is utilized to formulate the governing equations and corresponding boundary conditions. Numerical results are presented for the axial buckling of FG circular cylindrical microshells subject to simply-supported end conditions and the effects of material length scale parameter, material property gradient index, length-to-radius ratio and circumferential mode number on the size-dependent critical buckling load are extensively studied. For comparison purpose, the critical buckling loads predicted by modified couple stress theory (MCST) and classical theory (CT) are also presented. Results show that the size effect plays an important role for lower values of dimensionless length scale parameter. Moreover, it is observed that the critical buckling loads obtained based on MSGT are greater than those obtained based on MCST and CT.

Appendices

Appendix 1

The force resultants and moment resultants on the basis of Eq. (16) in terms of displacements are defined as

$$ \begin{aligned} N_{xx} & = A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{{\partial \psi_{x} }}{\partial x} + A_{12} \left( {\frac{\partial v}{\partial y} + \frac{w}{R}} \right) + B_{12} \frac{{\partial \psi_{y} }}{\partial y},\quad Q_{x} = k_{s} A_{55} \left( {\psi_{x} + {\mkern 1mu} \frac{\partial w}{\partial x}} \right), \\ N_{yy} & = A_{11} \left( {\frac{\partial v}{\partial y} + \frac{w}{R}} \right) + B_{11} \frac{{\partial \psi_{y} }}{\partial y} + A_{12} \frac{\partial u}{\partial x} + B_{12} \frac{{\partial \psi_{x} }}{\partial x},\quad Q_{y} = k_{s} A_{55} \left( {\frac{\partial w}{\partial y} + \psi_{y} - \frac{v}{R}} \right), \\ N_{xy} & = A_{55} \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right) + B_{55} \left( {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \right), \\ M_{xx} & = B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{{\partial \psi_{x} }}{\partial x} + B_{12} \left( {\frac{\partial v}{\partial y} + \frac{w}{R}} \right) + D_{12} \frac{{\partial \psi_{y} }}{\partial y}, \\ M_{yy} & = B_{11} \left( {\frac{\partial v}{\partial y} + \frac{w}{R}} \right) + D_{11} \frac{{\partial \psi_{y} }}{\partial y} + B_{12} \frac{\partial u}{\partial x} + D_{12} \frac{{\partial \psi_{x} }}{\partial x}, \\ M_{xy} & = B_{55} \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right) + D_{55} \left( {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \right). \\ \end{aligned} $$

(27)

$$ \begin{aligned} P_{x} & = 2A_{55} l_{0}^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial y} + \frac{1}{R}\frac{\partial w}{\partial x}} \right) + 2B_{55} l_{0}^{2} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{y} }}{\partial x\,\partial y}} \right), \\ P_{y} & = 2A_{55} l_{0}^{2} \left( {\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{1}{R}\frac{\partial w}{\partial y}} \right) + 2B_{55} l_{0}^{2} \left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ P_{z} & = 2A_{55} l_{0}^{2} \left( { - \frac{1}{R}\frac{\partial v}{\partial y} - \frac{w}{{R^{2} }} + \frac{{\partial \psi_{x} }}{\partial x} + \frac{{\partial \psi_{y} }}{\partial y}} \right), \\ M_{x}^{p} & = 2B_{55} l_{0}^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial y} + \frac{1}{R}\frac{\partial w}{\partial x}} \right) + 2D_{55} l_{0}^{2} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{y} }}{\partial x\partial y}} \right), \\ M_{y}^{p} & = 2B_{55} l_{0}^{2} \left( {\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{1}{R}\frac{\partial w}{\partial y}} \right) + 2D_{55} l_{0}^{2} \left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right). \\ \end{aligned} $$

(28)

$$ \begin{aligned} Y_{xx} & = A_{55} l_{2}^{2} \left( {\frac{{\partial \psi_{y} }}{\partial x} + \frac{1}{R}\frac{\partial v}{\partial x} - \frac{{\partial^{2} w}}{\partial x\partial y}} \right),\quad Y_{yy} = A_{55} l_{2}^{2} \left[ {\frac{1}{R}\left( {\frac{\partial u}{\partial y} - \frac{\partial v}{\partial x}} \right) + \frac{{\partial^{2} w}}{\partial x\partial y} - \frac{{\partial \psi_{x} }}{\partial y}} \right], \\ Y_{zz} & = A_{55} l_{2}^{2} \left( {\frac{{\partial \psi_{x} }}{\partial y} - \frac{{\partial \psi_{y} }}{\partial x} - \frac{1}{R}\frac{\partial u}{\partial y}} \right),\quad Y_{xy} = \frac{{A_{55} l_{2}^{2} }}{2}{\mkern 1mu} \left( {\frac{1}{R}{\mkern 1mu} \frac{\partial v}{\partial y} + \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial \psi_{x} }}{\partial x} + \frac{{\partial \psi_{y} }}{\partial y}} \right), \\ Y_{xz} & = \frac{{A_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} u}}{\partial x\partial y} - \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{v}{{R^{2} }} + \frac{1}{R}\frac{\partial w}{\partial y} + \frac{{\psi_{y} }}{R}} \right) + \frac{{B_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} - \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }}} \right), \\ Y_{yz} & = \frac{{A_{55} l_{2}^{2} }}{2}\left( {{\mkern 1mu} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\partial^{2} v}}{\partial x\partial y} - \frac{1}{R}\frac{\partial w}{\partial x} + \frac{{\psi_{x} }}{R}} \right) + \frac{{B_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} - \frac{{\partial^{2} \psi_{y} }}{\partial x\partial y}} \right), \\ H_{xz} & = \frac{{B_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} u}}{\partial x\partial y} - \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{v}{{R^{2} }} + \frac{1}{R}\frac{\partial w}{\partial y} + \frac{{\psi_{y} }}{R}} \right) + \frac{{D_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} - \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }}} \right), \\ H_{yz} & = \frac{{B_{55} l_{2}^{2} }}{2}\left( {{\mkern 1mu} \frac{{\partial^{2} u}}{{\partial y^{2} }} - {\mkern 1mu} \frac{{\partial^{2} v}}{\partial x\partial y} - \frac{1}{R}\frac{\partial w}{\partial x} + \frac{{\psi_{x} }}{R}} \right) + \frac{{D_{55} l_{2}^{2} }}{2}\left( {\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} - \frac{{\partial^{2} \psi_{y} }}{\partial x\partial y}} \right). \\ \end{aligned} $$

(29)

$$ \begin{aligned} T_{xxx} & = \frac{{2A_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} u}}{{\partial x^{2} }} - \frac{{\partial^{2} u}}{{\partial y^{2} }} - 2\frac{{\partial^{2} v}}{\partial x\partial y} - \frac{1}{R}\frac{\partial w}{\partial x}} \right) - \frac{{2B_{55} l_{1}^{2} }}{5}\left( {\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} - 2\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }}} \right), \\ T_{yyy} & = - \frac{{2A_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{{\partial^{2} v}}{{\partial x^{2} }} - 2\frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{3}{R}\frac{\partial w}{\partial y} + \frac{v}{{R^{2} }} - {\mkern 1mu} \frac{{\psi_{y} }}{R}} \right) - \frac{{2B_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ T_{xxy} & = \frac{{2A_{55} l_{1}^{2} }}{15}\left( {8\frac{{\partial^{2} u}}{\partial x\partial y} + 4\frac{{\partial^{2} v}}{{\partial x^{2} }} - 3\frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{2}{R}\frac{\partial w}{\partial y} - \frac{v}{{R^{2} }} + \frac{{\psi_{y} }}{R}} \right) + \frac{{2B_{55} l_{1}^{2} }}{15}\left( {4\frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} + 8\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} - 3\frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ T_{yyx} & = \frac{{2A_{55} l_{1}^{2} }}{15}\left( { - 3\frac{{\partial^{2} u}}{{\partial x^{2} }} + 4\frac{{\partial^{2} u}}{{\partial y^{2} }} + 8\frac{{\partial^{2} v}}{\partial x\partial y} + \frac{4}{R}\frac{\partial w}{\partial x}} \right) + \frac{{2B_{55} l_{1}^{2} }}{15}\left( {8\frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} - 3\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + 4\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }}} \right), \\ T_{zzy} & = \frac{{2A_{55} l_{1}^{2} }}{15}\left( { - 2\frac{{\partial^{2} u}}{\partial x\partial y} - {\mkern 1mu} \frac{{\partial^{2} v}}{{\partial x^{2} }} - 3\frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{7}{R}\frac{\partial w}{\partial y} + 4\frac{v}{{R^{2} }} - 4\frac{{\psi_{y} }}{R}} \right) - \frac{{2B_{55} l_{1}^{2} }}{15}\left( {\frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + 3\frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ T_{xxz} & = \frac{{2A_{55} l_{1}^{2} }}{15}\left( {\frac{2}{R}\frac{\partial v}{\partial y} + 4\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{w}{{R^{2} }} + 8\frac{{\partial \psi_{x} }}{\partial x} - 2\frac{{\partial \psi_{y} }}{\partial y}} \right), \\ T_{yyz} & = \frac{{2A_{55} l_{1}^{2} }}{15}{\mkern 1mu} \left( {4\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }} - 4\frac{w}{{R^{2} }} - \frac{8}{R}\frac{\partial v}{\partial y} + 8\frac{{\partial \psi_{y} }}{\partial y} - 2\frac{{\partial \psi_{x} }}{\partial x}} \right), \\ T_{xyz} & = \frac{{2A_{55} l_{1}^{2} }}{3}\left( { - \frac{1}{2R}\frac{\partial v}{\partial x} - \frac{1}{2R}\frac{\partial u}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x} + \frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial \psi_{x} }}{\partial y}} \right), \\ \end{aligned} $$

$$ \begin{aligned} M_{xxx} & = \frac{{2B_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} u}}{{\partial x^{2} }} - \frac{{\partial^{2} u}}{{\partial y^{2} }} - 2\frac{{\partial^{2} v}}{\partial x\partial y} - \frac{1}{R}\frac{\partial w}{\partial x}} \right) - \frac{{2D_{55} l_{1}^{2} }}{5}\left( {\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} - 2\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }}} \right), \\ M_{yyy} & = - \frac{{2B_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{{\partial^{2} v}}{{\partial x^{2} }} - 2\frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{3}{R}\frac{\partial w}{\partial y} + \frac{v}{{R^{2} }} - \frac{{\psi_{y} }}{R}} \right) - \frac{{2D_{55} l_{1}^{2} }}{5}\left( {2\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ M_{xxy} & = \frac{{2B_{55} l_{1}^{2} }}{15}\left( {8{\mkern 1mu} \frac{{\partial^{2} u}}{\partial x\partial y} + 4{\mkern 1mu} \frac{{\partial^{2} v}}{{\partial x^{2} }} - 3\frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{2}{R}\frac{\partial w}{\partial y} - {\mkern 1mu} \frac{v}{{R^{2} }} + {\mkern 1mu} \frac{{\psi_{y} }}{R}} \right) + \frac{{2D_{55} l_{1}^{2} }}{15}\left( {4\frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} + 8\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} - 3\frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right), \\ M_{yyx} & = \frac{{2B_{55} l_{1}^{2} }}{15}\left( { - 3\frac{{\partial^{2} u}}{{\partial x^{2} }} + 4\frac{{\partial^{2} u}}{{\partial y^{2} }} + 8\frac{{\partial^{2} v}}{\partial x\partial y} + \frac{4}{R}\frac{\partial w}{\partial x}} \right) + \frac{{2D_{55} l_{1}^{2} }}{15}\left( {8\frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} - 3\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + 4\frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }}} \right). \\ \end{aligned} $$

(30)

Appendix 2

$$ \begin{aligned} C_{1} & = \left( {2l_{0}^{2} + \frac{4}{5}{\mkern 1mu} l_{1}^{2} } \right),C_{2} = \left( {\frac{8}{15}l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{3} = \left( {2l_{0}^{2} + \frac{4}{3}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{4} = \left( {2l_{0}^{2} + \frac{4}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right), \\ C_{5} & = \left( {2l_{0}^{2} + \frac{2}{3}l_{1}^{2} - \frac{1}{2}l_{2}^{2} } \right),C_{6} = \left( {\frac{1}{3}l_{1}^{2} + l_{2}^{2} } \right),C_{7} = \left( {\frac{3}{5}{\mkern 1mu} l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{8} = \left( {2l_{0}^{2} - \frac{2}{5}l_{1}^{2} } \right), \\ C_{9} & = \left( {\frac{5}{4}{\mkern 1mu} l_{2}^{2} + \frac{2}{3}{\mkern 1mu} l_{1}^{2} } \right),C_{10} = \left( {\frac{14}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{11} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{44}{15}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{12} = \left( {\frac{3}{5}{\mkern 1mu} l_{1}^{2} + \frac{1}{2}{\mkern 1mu} l_{2}^{2} } \right), \\ C_{13} & = \left( {2{\mkern 1mu} l_{1}^{2} + 2{\mkern 1mu} l_{0}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{14} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{6}{5}{\mkern 1mu} l_{1}^{2} + \frac{3}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{15} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{34}{15}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right), \\ C_{16} & = \left( {\frac{{4{\mkern 1mu} }}{15}l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{17} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{2}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{2}{\mkern 1mu} l_{2}^{2} } \right),C_{18} = \left( {\frac{4}{5}{\mkern 1mu} l_{1}^{2} - \frac{3}{4}{\mkern 1mu} l_{2}^{2} } \right), \\ C_{19} & = \left( {2l_{0}^{2} + \frac{38}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{20} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{4}{15}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{21} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{16}{5}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}l_{2}^{2} } \right), \\ C_{22} & = \left( {2l_{0}^{2} + \frac{8}{15}{\mkern 1mu} l_{1}^{2} } \right),C_{23} = \left( {\frac{16}{15}l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{24} = \left( {2{\mkern 1mu} l_{0}^{2} - \frac{4}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{25} = \left( {2l_{0}^{2} + \frac{32}{15}{\mkern 1mu} l_{1}^{2} + \frac{1}{4}{\mkern 1mu} l_{2}^{2} } \right), \\ C_{26} & = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{4}{5}{\mkern 1mu} l_{1}^{2} - \frac{3}{4}{\mkern 1mu} l_{2}^{2} } \right),C_{27} = \left( {\frac{4}{3}{\mkern 1mu} l_{1}^{2} + l_{2}^{2} } \right),C_{28} = \left( {\frac{4}{15}{\mkern 1mu} l_{1}^{2} - \frac{1}{2}{\mkern 1mu} l_{2}^{2} } \right),C_{29} = \left( {2{\mkern 1mu} l_{0}^{2} + \frac{6}{5}l_{1}^{2} } \right). \\ \end{aligned} $$