Non-local theory solution to a 3-D rectangular crack in an infinite transversely isotropic elastic material

Abstract

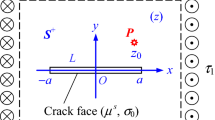
The non-local theory solution to a 3-D rectangular crack in an infinite transversely isotropic elastic material is proposed by means of the generalized Almansi’s theorem and the Schmidt method in the present paper. By using the Fourier transform and defining the jumps of displacement across the crack surface as the unknown variables, three pairs of dual integral equations are derived. To solve the dual integral equations, the jumps of displacement across the crack surface are expanded in a series of Jacobi polynomials. Numerical examples are provided to show the effects of the geometric shape of the rectangular crack and the lattice parameter of the material on the stress field near the crack edges. Unlike the classical solution, the present solution is no stress singularity along the rectangular crack edges, i.e. the stress field near the rectangular crack edges is finite. Therefore, we can use the maximum stress as a fracture criterion.

Appendix

The (38) and (39) can be rewritten as

$$ Ma + Mb = \left[ \begin{gathered} \bar{f}_{1} \hfill \\ \bar{f}_{2} \hfill \\ 0 \hfill \\ \end{gathered} \right],\quad Na - Nb = \left[ \begin{gathered} \bar{f}_{3} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(63)

where $M = \left[ {\begin{array}{*{20}c} {s\chi_{1}^{(1)} } & {s\chi_{2}^{(1)} } & t \\ {t\chi_{1}^{(1)} } & {t\chi_{2}^{(1)} } & { - s} \\ {\beta_{1}^{(1)} h_{1}^{*} } & {\beta_{2}^{(1)} h_{2}^{*} } & 0 \\ \end{array} } \right]$, $N = \left[ {\begin{array}{*{20}c} {\chi_{1}^{(2)} } & {\chi_{2}^{(2)} } & 0 \\ {\beta_{1}^{(2)} h_{1}^{*} } & {\beta_{2}^{(2)} h_{2}^{*} } & {\beta_{0}^{(2)} h_{0}^{*} } \\ {\beta_{1}^{(3)} h_{1}^{*} } & {\beta_{2}^{(3)} h_{2}^{*} } & {\beta_{0}^{(3)} h_{0}^{*} } \\ \end{array} } \right]$, $a = \left[ \begin{gathered} A_{1} \hfill \\ A_{2} \hfill \\ A_{3} \hfill \\ \end{gathered} \right]$, $b = \left[ \begin{gathered} B_{1} \hfill \\ B_{2} \hfill \\ B_{3} \hfill \\ \end{gathered} \right]$, A ₃ = A ₀ and B ₃ = −B ₀.

So it can be obtained that

$$ a = \frac{1}{2}M^{ - 1} \left[ \begin{gathered} \bar{f}_{1} \hfill \\ \bar{f}_{2} \hfill \\ 0 \hfill \\ \end{gathered} \right] + \frac{1}{2}N^{ - 1} \left[ \begin{gathered} \bar{f}_{3} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right],\quad b = \frac{1}{2}M^{ - 1} \left[ \begin{gathered} \bar{f}_{1} \hfill \\ \bar{f}_{2} \hfill \\ 0 \hfill \\ \end{gathered} \right] - \frac{1}{2}N^{ - 1} \left[ \begin{gathered} \bar{f}_{3} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(64)

So the unknown functions A _k and B _k can be expressed a

$$ A_{k} = \frac{1}{2}(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} + n_{k1} \bar{f}_{3} ),\quad B_{k} = \frac{1}{2}(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} - n_{k1} \bar{f}_{3} ) $$

(65)

where [m _kj ]_3×3 = [M]⁻¹, [n _kj ]_3×3 = [N]⁻¹.

Substituting (65) into (63), it can be obtained:

$$ \bar{f}_{1} \left[ {\begin{array}{*{20}c} {s\chi_{1}^{(1)} } & {s\chi_{2}^{(1)} } & t \\ {t\chi_{1}^{(1)} } & {t\chi_{2}^{(1)} } & { - s} \\ {\beta_{1}^{(1)} h_{1}^{*} } & {\beta_{2}^{(1)} h_{2}^{*} } & 0 \\ \end{array} } \right]\left[ \begin{gathered} m_{11} \hfill \\ m_{21} \hfill \\ m_{31} \hfill \\ \end{gathered} \right] + \bar{f}_{2} \left[ {\begin{array}{*{20}c} {s\chi_{1}^{(1)} } & {s\chi_{2}^{(1)} } & t \\ {t\chi_{1}^{(1)} } & {t\chi_{2}^{(1)} } & { - s} \\ {\beta_{1}^{(1)} h_{1}^{*} } & {\beta_{2}^{(1)} h_{2}^{*} } & 0 \\ \end{array} } \right]\left[ \begin{gathered} m_{12} \hfill \\ m_{22} \hfill \\ m_{32} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \bar{f}_{1} \hfill \\ \bar{f}_{2} \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(66)

$$ \bar{f}_{3} \left[ {\begin{array}{*{20}c} {\chi_{1}^{(2)} } & {\chi_{2}^{(2)} } & 0 \\ {\beta_{1}^{(2)} h_{1}^{*} } & {\beta_{2}^{(2)} h_{2}^{*} } & {\beta_{0}^{(2)} h_{0}^{*} } \\ {\beta_{1}^{(3)} h_{1}^{*} } & {\beta_{2}^{(3)} h_{2}^{*} } & {\beta_{0}^{(3)} h_{0}^{*} } \\ \end{array} } \right]\left[ \begin{gathered} n_{11} \hfill \\ n_{21} \hfill \\ n_{31} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \bar{f}_{3} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(67)

Therefore, we have

$$ \left[ {\begin{array}{*{20}c} {s\chi_{1}^{(1)} } & {s\chi_{2}^{(1)} } & t \\ {t\chi_{1}^{(1)} } & {t\chi_{2}^{(1)} } & { - s} \\ {\beta_{1}^{(1)} h_{1}^{*} } & {\beta_{2}^{(1)} h_{2}^{*} } & 0 \\ \end{array} } \right]\left\{ {\left[ \begin{gathered} m_{11} \hfill \\ m_{21} \hfill \\ m_{31} \hfill \\ \end{gathered} \right]\bar{f}_{1} + \left[ \begin{gathered} m_{12} \hfill \\ m_{22} \hfill \\ m_{32} \hfill \\ \end{gathered} \right]\bar{f}_{2} } \right\} = \left[ \begin{gathered} \bar{f}_{1} \hfill \\ \bar{f}_{2} \hfill \\ 0 \hfill \\ \end{gathered} \right] \Rightarrow \sum\limits_{k = 1}^{2} {\beta_{k}^{(1)} h_{k}^{*} (} m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} ) = 0 $$

(68)

$$ \left[ {\begin{array}{*{20}c} {\chi_{1}^{(2)} } & {\chi_{2}^{(2)} } & 0 \\ {\beta_{1}^{(2)} h_{1}^{*} } & {\beta_{2}^{(2)} h_{2}^{*} } & {\beta_{0}^{(2)} h_{0}^{*} } \\ {\beta_{1}^{(3)} h_{1}^{*} } & {\beta_{2}^{(3)} h_{2}^{*} } & {\beta_{0}^{(3)} h_{0}^{*} } \\ \end{array} } \right]\left[ \begin{gathered} n_{11} \hfill \\ n_{21} \hfill \\ n_{31} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 1 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right] \Rightarrow \left\{ \begin{gathered} \sum\limits_{k = 1}^{2} {\beta_{k}^{(2)} } h_{k}^{*} n_{k1} + \beta_{0}^{(2)} h_{0}^{*} n_{31} = 0 \hfill \\ \sum\limits_{k = 1}^{2} {\beta_{k}^{(3)} } h_{k}^{*} n_{k1} + \beta_{0}^{(3)} h_{0}^{*} n_{31} = 0 \hfill \\ \end{gathered} \right. $$

(69)

Substituting (65) into (35) and applying (68) and (69), we have

$$ \begin{aligned} \sigma_{zz}^{ * (1)} (x,y,0) & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\sum\limits_{k = 1}^{2} {\beta_{k}^{(1)} (s,t)h_{k}^{*} (p,s,t)} } \,\times\,(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} + n_{k1} \bar{f}_{3} )} \cos (sx)\cos (ty)dsdt \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\sum\limits_{k = 1}^{2} {\beta_{k}^{(1)} (s,t)h_{k}^{*} (p,s,t)} }\,\times\, n_{k1} \bar{f}_{3} \cos (sx)\cos (ty)dsdt} \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {g_{1} (p,s,t)} \,\times\,\bar{f}_{3} \cos (sx)\cos (ty)dsdt} \\ \end{aligned} $$

(70)

$$ \begin{aligned} \sigma_{xz}^{ * (1)} (x,y,0) & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\left[ {\sum\limits_{k = 1}^{2} {\beta_{k}^{(2)} (s,t)h_{k}^{*} (p,s,t)(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} + n_{k1} \bar{f}_{3} )} } \right.} } \\ & \quad \left. { + \beta_{0}^{(2)} (s,t)h_{0}^{*} (p,s,t)n_{31} \bar{f}_{3} } \right]\sin (sx)\cos (ty)dsdt \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\sum\limits_{k = 1}^{2} {\beta_{k}^{(2)} (s,t)h_{k}^{*} (p,s,t)} } (m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} )\sin (sx)\cos (ty)dsdt} \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } [ g_{2} (p,s,t)\bar{f}_{1} + g_{3} (p,s,t)\bar{f}_{2} ]\sin (sx)\cos (ty)dsdt} \\ \end{aligned} $$

(71)

$$ \begin{aligned} \sigma_{yz}^{ * (1)} (x,y,0) & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\left[ {\sum\limits_{k = 1}^{2} {\beta_{k}^{(3)} (s,t)h_{k}^{*} (p,s,t)(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} + n_{k1} \bar{f}_{3} )} } \right.} } \\ & \quad \left. { + \beta_{0}^{(3)} (s,t)h_{0}^{*} (p,s,t)n_{31} \bar{f}_{3} } \right]\cos (sx)\sin (ty)dsdt \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } {\sum\limits_{k = 1}^{2} {\beta_{k}^{(3)} (s,t)} } h_{k}^{*} (p,s,t)(m_{k1} \bar{f}_{1} + m_{k2} \bar{f}_{2} )\cos (sx)\sin (ty)dsdt} \\ & = \frac{2}{{\pi^{2} }}\int_{0}^{\infty } {\int_{0}^{\infty } [ g_{4} (p,s,t)\bar{f}_{1} + g_{5} (p,s,t)\bar{f}_{2} ]\cos (sx)\sin (ty)dsdt} \\ \end{aligned} $$

(72)