Skip to main content
SpringerLink
Log in

Application of the differential quadrature method to free vibration of viscoelastic thin plate with linear thickness variation

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

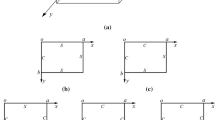
The differential quadrature method has been applied to investigate vibrations of viscoelastic thin plate with variable thickness. Firstly, the governing equations are derived in terms of the thin-plate theory and the two-dimensional viscoelastic differential constitutive relation. Then, the convergence of the method is demonstrated based on the differential equation of uniform thickness elastic square plate, which is reduced from the differential equation of viscoelastic plate with varying thickness. Lastly, the effects of aspect ratio, thickness ratio and dimensionless delay time on the vibrations of the linear thickness viscoelastic plate with different boundary conditions have been studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Aksu G, Al-Kaabi SA (1987) Free vibration analysis of Mindlin plates with linearly varying thickness. J Sound Vib 119:189–205

    Article  ADS  Google Scholar 

  2. Mizusawa T (1993) Vibration of rectangular Mindlin plates with tapered thickness by the spline strip method. Comput Struct 46:451–463

    Article  ADS  Google Scholar 

  3. Sakiyama T, Huang M (1998) Free vibration analysis of rectangular plates with variable thickness. J Sound Vib 216:379–397

    Article  ADS  Google Scholar 

  4. Mizusawa T, Kondo Y (2001) Application of the spline element method to analyze vibration of skew Mindlin plates with varying thickness in one direction. J Sound Vib 241:485–501

    Article  ADS  Google Scholar 

  5. Zenkour AM, Mashat DS (2009) Exact solutions for variable-thickness inhomogeneous elastic plates under various boundary conditions. Meccanica 44:433–447

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhou YF, Wang ZM (2008) Vibrations of axially moving viscoelastic plate with parabolically varying thickness. J Sound Vib 316:198–210

    Article  ADS  Google Scholar 

  7. Zhou YF, Wang ZM (2009) Dynamic behaviors of axially moving viscoelastic plate with varying thickness. Chin J Mech Eng 22(2):276–281

    Article  Google Scholar 

  8. Flügge W (1975) Viscoelasticity, 2nd edn. Springer, Berlin

    Book  MATH  Google Scholar 

  9. Malekzadeh P, Karami G (2004) Vibration of non-uniform thick plates on elastic foundation by differential quadrature method. Eng Struct 26:1473–1482

    Article  Google Scholar 

  10. Fu YM, Chen Y, Zhang P (2013) Thermal buckling analysis of functionally graded beam with longitudinal crack. Meccanica 48:1227–1237

    Article  MathSciNet  MATH  Google Scholar 

  11. Gorman DJ (1982) Free vibration analysis of rectangular plates. Elsevier North Holland Inc, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Instrument Science & Opto-electronics Engineering, Beijing University of Aeronautics & Astronautics, Beijing, 100191, China

    Yin Feng Zhou

  2. School of Civil Engineering and Architecture, Xi’an University of Technology, Xi’an, 710048, China

    Zhong Min Wang

Authors
  1. Yin Feng Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhong Min Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yin Feng Zhou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, Y.F., Wang, Z.M. Application of the differential quadrature method to free vibration of viscoelastic thin plate with linear thickness variation. Meccanica 49, 2817–2828 (2014). https://doi.org/10.1007/s11012-014-0043-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0043-6

Keywords

Search

Navigation