Skip to main content
SpringerLink
Log in

A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

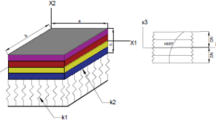
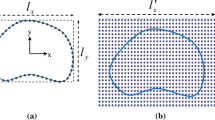
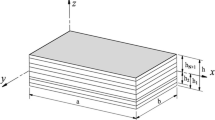
This paper deals with the static and dynamic analyses of multi-layered plates with discontinuities. The two-dimensional first-order shear deformation theory is used to derive the fundamental system of equations in terms of generalized displacements. The fundamental set, with its boundary conditions, is solved in its strong form. A new method termed strong formulation finite element method is considered in the present paper to solve this kind of plates. This numerical methodology is the cohesion of derivative evaluation of partial differential systems of equations and a domain sub-division. The numerical results in terms of natural frequencies and maximum deflections are compared to literature and to the same results obtained with a finite element code. The stability, accuracy and reliability of the present methodology is shown through several numerical applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Pagano NJ (1994) Exact solutions for rectangular bidirectional composites and sandwich plates. In: Reddy JN (ed) Mechanics of composite materials, vol 34., Solid mechanics and its applicationsSpringer, Dordrecht, pp 86–101

    Chapter  Google Scholar 

  2. Wang CM, Ang KK, Yang L, Watanabe E (2001) Vibration analysis of arbitrarily shaped sandwich plates via Ritz method. Mech Compos Mater Struct 8:101–118

    Article  Google Scholar 

  3. Reddy JN (2003) Mechanics of laminated composite plates and shells. CRC Press, Boca Raton

    Google Scholar 

  4. Ferreira AJM (2008) MATLAB codes for finite element analysis: solids and structures., Solid mechanics and its applicationsSpringer, New York

    Google Scholar 

  5. Ferreira AJM, Castro LMS, Bertoluzza S (2011) Analysis of plates on winkler foundation by wavelet collocation. Meccanica 46(4):865–873

    Article  MATH  Google Scholar 

  6. Akbarzadeh AH, Abbasi M, Hosseinizad SK, Eslami MR (2011) Dynamic analysis of functionally graded plates using the hybrid Fourier-Laplace transform under thermomechanical loading. Meccanica 46(6):1373–1392

    Article  MATH  MathSciNet  Google Scholar 

  7. Jedrysiak J, Radzikowska A (2012) Tolerance averaging of heat conduction in transversally graded laminates. Meccanica 47(1):95–107

    Article  MathSciNet  Google Scholar 

  8. Yas MH, Jodaei A, Irandoust S, Nasiri Aghdam M (2012) Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates on elastic foundations. Meccanica 47(6):1401–1423

    Article  MathSciNet  Google Scholar 

  9. Roque CMC, Rodrigues JD, Ferreira AJM (2012) Analysis of thick plates by local radial basis functions-finite differences method. Meccanica 47(5):1157–1171

    Article  MathSciNet  Google Scholar 

  10. Malekzadeh P, Golbahar Haghighi MR, Alibeygi Beni A (2012) Buckling analysis of functionally graded arbitrary straight-sided quadrilateral plates on elastic foundations. Meccanica 47(2):321–333

    Article  MathSciNet  Google Scholar 

  11. Asemi K, Akhlaghi M, Salehi M (2012) Dynamic analysis of thick short length FGM cylinders. Meccanica 47(6):1441–1453

    Article  MathSciNet  Google Scholar 

  12. Michalak B, Wirowski A (2012) Dynamic modelling of thin plate made of certain functionally graded materials. Meccanica 47(6):1487–1498

    Article  Google Scholar 

  13. Liu B, Xing YF, Eisenberger M, Ferreira AJM (2014) Thickness-shear vibration analysis of rectangular quartz plates by a numerical extended Kantorovich method. Compos Struct 107:429–435

    Article  Google Scholar 

  14. Gottlieb D, Orszag SA (1997) Numerical analysis of spectral methods: theory and applications. In: CBMS-NSF regional conference series in applied mathematics. Society for Industrial and Applied Mathematics, Philadelphia

  15. Shu C (1991) Generalized differential: integral quadrature and application to the simulation of incompressible viscous flows including parallel computation. PhD thesis, Glasgow University, Glasgow

  16. Boyd JP (2001) Chebyshev and Fourier spectral methods, 2nd edn. Dover, Mineola

    MATH  Google Scholar 

  17. Canuto C, Hussaini MY, Quarteroni A, Zang TA (2006) Spectral method: fundamentals in single domains. Springer, New York

    Google Scholar 

  18. Kansa EJ (1990) Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-i surface approximations and partial derivative estimates. Comput. Math. Appl. 19(8–9):127–145

    Article  MATH  MathSciNet  Google Scholar 

  19. Kansa EJ (1990) Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics-ii solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 19(8–9):147–161

    Article  MATH  MathSciNet  Google Scholar 

  20. Wendland H (1995) Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 4(1):389–396

    Article  MATH  MathSciNet  Google Scholar 

  21. Wendland H (1998) Error estimates for interpolation by compactly supported radial basis functions of minimal degree. J Approx Theory 93(2):258–272

    Article  MATH  MathSciNet  Google Scholar 

  22. Wendland H (1999) Meshless Galerkin methods using radial basis functions. Math Comput 68(228):1521–1531

    Article  MATH  MathSciNet  ADS  Google Scholar 

  23. Fasshauer GE (1999) Solving differential equations with radial basis functions: multilevel methods and smoothing. Adv Comput Math 11(2–3):139–159

    Article  MATH  MathSciNet  Google Scholar 

  24. Buhmann MD (2003) Radial basis functions. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  25. Ferreira AJM, Roque CMC, Martins PALS (2003) Analysis of composite plates using higher-order shear deformation theory and a finite point formulation based on the multiquadric radial basis function method. Compos Part B 34(7):627–636

    Article  Google Scholar 

  26. Ferreira AJM, Roque CMC, Jorge RMN (2005) Analysis of composite plates by trigonometric shear deformation theory and multiquadrics. Comput Struct 83(27):2225–2237

    Article  Google Scholar 

  27. Fasshauer GE, Zhang JG (2007) On choosing “optimal” shape parameters for RBF approximation. Numer Algorithms, 45(1–4):345–368. cited By (since 1996)55.

  28. Xiang S, Wang K-M (2009) Free vibration analysis of symmetric laminated composite plates by trigonometric shear deformation theory and inverse multiquadric RBF. Thin-Walled Struct 47(3):304–310

    Article  MathSciNet  Google Scholar 

  29. Xiang S, Jiang S-X, Bi Z-Y, Jin Y-X, Yang M-S (2011) A nth-order meshless generalization of Reddy’s third-order shear deformation theory for the free vibration on laminated composite plates. Compos Struct 93(2):299–307

    Article  Google Scholar 

  30. Rodrigues JD, Roque CMC, Ferreira AJM, Carrera E, Cinefra M (2011) Radial basis functions-finite differences collocation and a unified formulation for bending, vibration and buckling analysis of laminated plates, according to Murakami’s zig-zag theory. Compos Struct 93(7):1613–1620

    Article  Google Scholar 

  31. Ferreira AJM, Roque CMC, Neves AMA, Jorge RMN, Soares CMM, Liew KM (2011) Buckling and vibration analysis of isotropic and laminated plates by radial basis functions. Compos Part B 42(3):592–606

    Article  Google Scholar 

  32. Ferreira AJM, Carrera E, Cinefra M, Roque CMC, Polit O (2011) Analysis of laminated shells by a sinusoidal shear deformation theory and radial basis functions collocation, accounting for through-the-thickness deformations. Compos Part B 42:1276–1284

    Article  Google Scholar 

  33. Gherlone M, Iurlaro L, Di Sciuva M (2012) A novel algorithm for shape parameter selection in radial basis functions collocation method. Compos Struct 94(2):453–461

    Article  Google Scholar 

  34. Neves AMA, Ferreira AJM, Carrera E, Cinefra M, Roque CMC, Jorge RMN, Soares CMM (2012) A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos Struct 94(5):1814–1825

    Article  Google Scholar 

  35. Giunta G, Biscani F, Belouettar S, Ferreira AJM, Carrera E (2013) Free vibration analysis of composite beams via refined theories. Compos Part B 44(1):540–552

    Article  Google Scholar 

  36. Tornabene F, Fantuzzi N, Viola E, Ferreira AJM (2013) Radial basis function method applied to doubly-curved laminated composite shells and panels with a general higher-order equivalent single layer theory. Compos Part B 55:642–659

    Article  Google Scholar 

  37. Iurlaro L, Gherlone M, Di Sciuva M (2014) Energy based approach for shape parameter selection in radial basis functions collocation method. Compos Struct 107:70–78

    Article  Google Scholar 

  38. Maturi DA, Ferreira AJM, Zenkour AM, Mashat DS (2014) Analysis of sandwich plates with a new layerwise formulation. Compos Part B 56:484–489

    Article  Google Scholar 

  39. Bert CW, Malik M (1996) The differential quadrature method for irregular domains and application to plate vibration. Int J Mech Sci 38(6):589–606

    Article  MATH  Google Scholar 

  40. Shu C, Chew YT (1999) Application of multi-domain GDQ method to analysis of waveguides with rectangular boundaries. Prog Electromagn Res 21:1–19

    Article  Google Scholar 

  41. Shu C (2000) Differential quadrature and its applications in engineering. Springer, New York

    Book  Google Scholar 

  42. Shu C, Chen W, Du H (2000) Free vibration analysis of curvilinear quadrilateral plates by the differential quadrature method. J Comput Phys 163(2):452–466

    Article  MATH  ADS  Google Scholar 

  43. Karami G, Malekzadeh P (2003) Application of a new differential quadrature methodology for free vibration analysis of plates. Int J Numer Methods Eng 56(6):847–868

    Article  MATH  Google Scholar 

  44. Viola E, Tornabene F (2005) Vibration analysis of damaged circular arches with varying cross-section. Struct Integr Durab (SID-SDHM) 1(2):155–169

    Google Scholar 

  45. Viola E, Tornabene F (2006) Vibration analysis of conical shell structures using GDQ method. Far East J Appl Math 25(1):23–39

    MATH  MathSciNet  Google Scholar 

  46. Tornabene F (2007) Modellazione e soluzione di strutture a guscio in materiale anisotropo. PhD thesis, University of Bologna, Bologna

  47. Tornabene F, Viola E (2007) Vibration analysis of spherical structural elements using the GDQ method. Comput Math Appl 53(10):1538–1560

    Article  MATH  MathSciNet  Google Scholar 

  48. Viola E, Dilena M, Tornabene F (2007) Analytical and numerical results for vibration analysis of multi-stepped and multi-damaged circular arches. J Sound Vib 299(1–2):143–163

    Article  ADS  Google Scholar 

  49. Marzani A, Tornabene F, Viola E (2008) Nonconservative stability problems via generalized differential quadrature method. J Sound Vib 315(1–2):176–196

    Article  ADS  Google Scholar 

  50. Tornabene F, Viola E (2008) 2D solution for free vibrations of parabolic shells using generalized differential quadrature method. Eur J Mech 27(6):1001–1025

    Article  MATH  Google Scholar 

  51. Tornabene F, Viola E (2009) Free vibration analysis of functionally graded panels and shells of revolution. Meccanica 44(3):255–281

    Article  MATH  Google Scholar 

  52. Viola E, Tornabene F (2009) Free vibrations of three parameter functionally graded parabolic panels of revolution. Mech Res Commun 36(5):587–594

    Article  MATH  Google Scholar 

  53. Tornabene F, Viola E (2009) Free vibrations of four-parameter functionally graded parabolic panels and shells of revolution. Eur J Mech 28(5):991–1013

    Article  MATH  Google Scholar 

  54. Tornabene F (2009) Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput Methods Appl Mech Eng 198(37–40):2911–2935

    Article  MATH  ADS  Google Scholar 

  55. Tornabene F, Viola E, Inman DJ (2009) 2D differential quadrature solution for vibration analysis of functionally graded conical, cylindrical shell and annular plate structures. J Sound Vib 328(3):259–290

    Article  ADS  Google Scholar 

  56. Tornabene F, Marzani A, Viola E, Elishakoff I (2010) Critical flow speeds of pipes conveying fluid by the generalized differential quadrature method. Adv Theor Appl Mech 3(3):121–138

    MATH  Google Scholar 

  57. Tornabene F, Liverani A, Caligiana G (2011) FGM and laminated doubly-curved shells and panels of revolution with a free-form meridian: a 2D GDQ solution for free vibrations. Int J Mech Sci 53:446–470

    Article  Google Scholar 

  58. Tornabene F (2011) Free vibrations of laminated composite doubly-curved shells and panels of revolution via the GDQ method. Comput Methods Appl Mech Eng 200:931–952

    Article  MATH  MathSciNet  ADS  Google Scholar 

  59. Malekzadeh P, Golbahar Haghighi MR, Atashi MM (2011) Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment. Meccanica 46(5):893–913

    Article  MATH  MathSciNet  Google Scholar 

  60. Tornabene F (2011) 2D GDQ solution for free vibrations of anisotropic doubly-curved shells and panels of revolution. Compos Struct 93:1854–1876

    Article  Google Scholar 

  61. Tornabene F (2011) Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler–Pasternak elastic foundations. Compos Struct 94:186–206

    Article  Google Scholar 

  62. Soleimani S, Qajarjazi A, Bararnia H, Barari A, Domairry G (2011) Entropy generation due to natural convection in a partially heated cavity by local RBF-DQ method. Meccanica 46(5):1023–1033

    Article  MATH  Google Scholar 

  63. Viola E, Rossetti L, Fantuzzi N (2012) Numerical investigation of functionally graded cylindrical shells and panels using the generalized unconstrained third order theory coupled with the stress recovery. Compos Struct 94:3736–3758

    Article  Google Scholar 

  64. Tornabene F, Liverani A, Caligiana G (2012) Laminated composite rectangular and annular plates: a GDQ solution for static analysis with a posteriori shear and normal stress recovery. Compos Part B 43:1847–1872

    Article  Google Scholar 

  65. Tornabene F, Liverani A, Caligiana G (2012) Static analysis of laminated composite curved shells and panels of revolution with a posteriori shear and normal stress recovery using generalized differential quadrature method. Int J Mech Sci 61:71–87

    Article  Google Scholar 

  66. Tornabene F, Liverani A, Caligiana G (2012) General anisotropic doubly-curved shell theory: a differential quadrature solution for free vibrations of shells and panels of revolution with a free-form meridian. J Sound Vib 331:4848–4869

    Article  ADS  Google Scholar 

  67. Tornabene F (2012) Meccanica delle strutture a guscio in materiale composito. Il Metodo generalizzato di quadratura differenziale. Esculapio, New York

    Book  Google Scholar 

  68. Tornabene F, Ceruti A (2013) Free-form laminated doubly-curved shells and panels of revolution on Winkler–Pasternak elastic foundations: A 2D GDQ solution for static and free vibration analysis. World J Mech 3:1–25

    Article  Google Scholar 

  69. Tornabene F, Viola E, Fantuzzi N (2013) General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos Struct 104:94–117

    Article  Google Scholar 

  70. Eftekhari SA, Jafari AA (2014) A mixed modal-differential quadrature method for free and forced vibration of beams in contact with fluid. Meccanica 49:535–564

    Article  MATH  MathSciNet  Google Scholar 

  71. Tornabene F, Ceruti A (2013) Mixed static and dynamic optimizazion of four-parameter functionally graded completely doubly-curved and degenerate shells and panels using GDQ method. Math Probl Eng 2013:1–33. Article ID 867079, http://dx.doi.org/10.1155/2013/867079

  72. Tornabene F, Viola E (2013) Static analysis of functionally graded doubly-curved shells and panels of revolution. Meccanica 48:901–930

    Article  MathSciNet  Google Scholar 

  73. Viola E, Tornabene F, Fantuzzi N (2013) General higher-order shear deformation theories for the free vibration analysis of completely doubly-curved laminated shells and panels. Compos Struct 95:639–666

    Article  Google Scholar 

  74. Viola E, Tornabene F, Fantuzzi N (2013) Static analysis of completely doubly-curved laminated shells and panels using general higher-order shear deformation theories. Compos Struct 101:59–93

    Article  Google Scholar 

  75. Ferreira AJM, Viola E, Tornabene F, Fantuzzi N, Zenkour AM (2013) Analysis of sandwich plates by generalized differential quadrature method. Math Probl Eng 2013:1–12. Article ID 964367. http://dx.doi.org/10.1155/2013/964367

  76. Tornabene F, Reddy JN (2013) FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundation: a GDQ solution for static analysis with a posteriori stress and strain recovery. J Indian Inst Sci 93(4):635–688

    MathSciNet  Google Scholar 

  77. Tornabene F, Fantuzzi N, Viola E, Reddy JN (2014) Winkler–Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos Part B 57:269–296

    Article  Google Scholar 

  78. Eftekhari SA, Jafari AA (2013) A simple and accurate mixed FE-DQ formulation for free vibration of rectangular and skew mindlin plates with general boundary conditions. Meccanica 48(5):1139–1160

    Article  MathSciNet  Google Scholar 

  79. Tornabene F, Fantuzzi N, Viola E, Carrera E (2014) Static analysis of doubly-curved anisotropic shells and panels using CUF approach, differential geometry and differential quadrature method. Compos Struct 107:675–697

    Article  Google Scholar 

  80. Ferreira AJM, Carrera E, Cinefra M, Viola E, Tornabene F, Fantuzzi N, Zenkour AM (2014) Analysis of thick isotropic and cross-ply laminated plates by generalized differential quadrature method and a unified formulation. Compos Part B 58:544–552

    Article  Google Scholar 

  81. Viola E, Rossetti L, Fantuzzi N, Tornabene F (2014) Static analysis of functionally graded conical shells and panels using the generalized unconstrained third order theory coupled with the stress recovery. Compos Struct 112(1):44–65

    Article  Google Scholar 

  82. Tornabene F, Fantuzzi N (2014) Mechanics of laminated composite doubly-curved shell structures. Esculapio, New York

    Book  Google Scholar 

  83. Cottrell JA, Reali A, Bazilevs Y, Hughes TJR (2006) Isogeometric analysis of structural vibrations. Comput Methods Appl Mech Eng 195(41–43):5257–5296

    Article  MATH  MathSciNet  ADS  Google Scholar 

  84. Schillinger D, Evans JA, Reali A, Scott MA, Hughes TJR (2013) Isogeometric collocation: cost comparison with Galerkin methods and extension to adaptive hierarchical NURBS discretizations. Comput Methods Appl Mech Eng 267:170–232

    Article  MATH  MathSciNet  ADS  Google Scholar 

  85. Nguyen-Xuan H, Thai CH, Nguyen-Thoi T (2013) Isogeometric finite element analysis of composite sandwich plates using a higher order shear deformation theory. Compos Part B 55:558–574

    Article  Google Scholar 

  86. Evans JA, Hughes TJR (2013) Isogeometric divergence-conforming B-splines for the Darcy–Stokes–Brinkman equations. Math Models Methods Appl Sci 23(4):671–741

    Article  MATH  MathSciNet  Google Scholar 

  87. Thai CH, Ferreira AJM, Carrera E, Nguyen-Xuan H (2013) Isogeometric analysis of laminated composite and sandwich plates using a layerwise deformation theory. Compos Struct 104:196–214

    Article  Google Scholar 

  88. Patera AT (1984) A spectral element method for fluid dynamics: laminar flow in a channel expansion. J Comput Phys 54(3):468–488

    Article  MATH  MathSciNet  ADS  Google Scholar 

  89. Funaro D (1986) A multidomain spectral approximation of elliptic equations. Numer Methods Partial Differ Equ 2(3):187–205

    Article  MATH  MathSciNet  Google Scholar 

  90. Quarteroni A (1987) Domain decomposition techniques using spectral methods. Calcolo 24(2):141–177

    Article  MATH  MathSciNet  Google Scholar 

  91. Gonzalez David, Cueto Elias, Doblare Manuel (2009) Towards an isogeometric meshless natural element method. Comput Methods Appl Sci 11:237–257

    MathSciNet  Google Scholar 

  92. Fischer P, Mergheim J, Steinmann P (2010) On the c1 continuous discretization of non-linear gradient elasticity: a comparison of nem and fem based on bernstein-bezier patches. Int J Numer Methods Eng 82:1282–1307

    MATH  MathSciNet  Google Scholar 

  93. Rajagopal Amirtham, Fischer Paul, Kuhl Ellen, Steinmann Paul (2010) Natural element analysis of the Cahn–Hilliard phase-field model. Comput Mech 46:471–493

    Article  MATH  MathSciNet  Google Scholar 

  94. Striz AG, Chen WL, Bert CW (1994) Static analysis of structures by the quadrature element method (QEM). Int J Solids Struct 31(20):2807–2818

    Article  MATH  Google Scholar 

  95. Striz AG, Chen WL, Bert CW (1997) Free vibration of plates by the high accuracy quadrature element method. J Sound Vib 202(5):689–702

    Article  MATH  ADS  Google Scholar 

  96. Wang X, Gu H (1997) Static analysis of frame structures by the differential quadrature element method. Int J Numer Methods Eng 40(4):759–772

    Article  MATH  Google Scholar 

  97. Zhong H, He Y (1998) Solution of poisson and laplace equations by quadrilateral quadrature element. Int J Solids Struct 35(21):2805–2819

    Article  MATH  Google Scholar 

  98. Wang X, Wang Y-L, Chen R-B (1998) Static and free vibrational analysis of rectangular plates by the differential quadrature element method. Commun Numer Methods Eng 14(12):1133–1141

    Article  MATH  Google Scholar 

  99. Liu FL, Liew KM (1998) Static analysis of reissner-mindlin plates by differential quadrature element method. J Appl Mech ASME 65:705–710

    Article  Google Scholar 

  100. Liu F-L, Liew KM (1999) Vibration analysis of discontinuous mindlin plates by differential quadrature element method. J Vib Acoust 121:204–208

    Article  Google Scholar 

  101. Liu F-L (1999) Differential quadrature element method for static analysis of shear deformable cross-ply laminates. Int J Numer Methods Eng 46(8):1203–1219

    Article  MATH  Google Scholar 

  102. Chen C-N (1999) The differential quadrature element method irregular element torsion analysis model. Appl Math Model 23(4):309–328

    Article  MATH  Google Scholar 

  103. Chen C-N (1999) The development of irregular elements for differential quadrature element method steady-state heat conduction analysis. Comput Methods Appl Mech Eng 170(1–2):1–14

    MATH  ADS  Google Scholar 

  104. Chen C-N (2000) A generalized differential quadrature element method. Comput Methods Appl Mech Eng 188(1–3):553–566

    Article  MATH  ADS  Google Scholar 

  105. Chen C-N (2003) DQEM and DQFDM for the analysis of composite two-dimensional elasticity problems. Compos Struct 59(1):3–13

    Article  Google Scholar 

  106. Zong Z, Lam KY, Zhang YY (2005) A multidomain differential quadrature approach to plane elastic problems with material discontinuity. Math Comput Model 41(4–5):539–553

    Article  MATH  MathSciNet  Google Scholar 

  107. Xing Y, Liu B (2009) High-accuracy differential quadrature finite element method and its application to free vibrations of thin plate with curvilinear domain. Int J Numer Methods Eng 80(13):1718–1742

    Article  MATH  MathSciNet  Google Scholar 

  108. Zhong H, Yu T (2009) A weak form quadrature element method for plane elasticity problems. Appl Math Model 33(10):3801–3814

    Article  MATH  MathSciNet  Google Scholar 

  109. Zong Z, Zhang Y (2009) Advanced differential quadrature methods. Chapman & Hall/CRC Applied Mathematics & Nonlinear Science. Taylor & Francis

  110. Xing Y, Liu B, Liu G (2010) A differential quadrature finite element method. Int J Appl Mech 2:207–227

    Article  Google Scholar 

  111. Fantuzzi N (2013) Generalized differential quadrature finite element method applied to advanced structural mechanics. PhD thesis, University of Bologna, Bologna

  112. Viola E, Tornabene F, Fantuzzi N (2013) Generalized differential quadrature finite element method for cracked composite structures of arbitrary shape. Compos Struct 106:815–834

    Article  Google Scholar 

  113. Fantuzzi N, Tornabene F, Viola E (2014) Generalized differential quadrature finite element method for vibration analysis of arbitrarily shaped membranes. Int J Mech Sci 79:216–251

    Article  Google Scholar 

  114. Fantuzzi N, Tornabene F (2014) Strong formulation finite element method for arbitrarily shaped laminated plates - I. Theoretical analysis. Adv Aircr Spacecr Sci 1(2):125–143

    Google Scholar 

  115. Fantuzzi N, Tornabene F (2014) Strong formulation finite element method for arbitrarily shaped laminated plates II. Numerical analysis. Adv Aircr Spacecr Science 1(2):145–175

    Google Scholar 

  116. Matuszyk Pawel J, Demkowicz Leszek F (2013) Parametric finite elements, exact sequences and perfectly matched layers. Comput Mech 51:35–45

    Article  MATH  MathSciNet  Google Scholar 

  117. Viola E, Tornabene F, Ferretti E, Fantuzzi N (2013) Soft core plane state structures under static loads using GDQFEM and cell method. Comput Model Eng Sci 94:301–329

    MathSciNet  Google Scholar 

  118. Viola E, Tornabene F, Ferretti E, Fantuzzi N (2013) On static analysis of composite plane state structures via GDQFEM and cell method. Comput Model Eng Sci 94:421–458

    MathSciNet  Google Scholar 

  119. Viola E, Tornabene F, Ferretti E, Fantuzzi N (2013) GDQFEM numerical simulations of continuous media with cracks and discontinuities. Comput Model Eng Sci 94:331–369

    MathSciNet  Google Scholar 

  120. Hughes TJR (2000) The finite element method: linear static and dynamic finite element analysis., Dover civil and mechanical engineering seriesDover Publications, Mineola

    Google Scholar 

  121. Evans JA, Hughes TJR (2012) Discrete spectrum analyses for various mixed discretizations of the Stokes eigenproblem. Comput Mech 50(6):667–674

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The research topic is one of the subjects of the Center of Study and Research for the Identification of Materials and Structures (CIMEST)-“M. Capurso” of the University of Bologna (Italy).

Author information

Authors and Affiliations

  1. DICAM Department, University of Bologna, Viale del Risorgimento 2, 40136, Bologna, Italy

    Nicholas Fantuzzi, Francesco Tornabene & Erasmo Viola

  2. Faculdade de Engenharia da Universidade do Porto, Porto, Portugal

    A. J. M. Ferreira

  3. Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O. Box 80203, Jeddah, 21589, Saudi Arabia

    A. J. M. Ferreira

Authors
  1. Nicholas Fantuzzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francesco Tornabene
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erasmo Viola
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. J. M. Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francesco Tornabene.

Additional information

Preliminary results were presented by the authors at the XXI° National Conference of Italian Association of Theoretical and Applied Mechanics (AIMETA 2013)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fantuzzi, N., Tornabene, F., Viola, E. et al. A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape. Meccanica 49, 2503–2542 (2014). https://doi.org/10.1007/s11012-014-0014-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0014-y

Keywords

Search

Navigation