Skip to main content
SpringerLink
Log in

Kinematic analysis of a 5-R SP parallel mechanism with centralized motion

  • Parallel Manipulators
  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

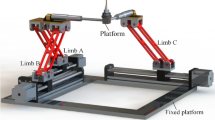
The paper presents a kinematic analysis of a parallel mechanism, referred to here as a mechanism with centralized motion. The paper includes a proof, based on the geometry of the mechanism, that the platform exhibits centralized motion. An interesting feature of this parallel mechanism is that it is partially collapsible which may be beneficial in practical applications where storage space is limited. The platform is connected to a base, regarded as fixed in this paper, by five identical legs where each leg is a three-link chain connected by a revolute joint, a spherical joint, and a prismatic joint. The result is that the platform has a screw motion about an axis which is perpendicular to the base and passes through the centroids of the base and the platform, for all positions of the platform. The pitch of the instantaneous screw depends on the platform assembly configuration and is a function of the platform position and orientation. To complete the kinematic study, the paper includes closed-form solutions to the inverse and forward position and velocity problems. Finally, the paper includes several numerical examples to illustrate some of the key features of this novel parallel mechanism.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gough VE, Whitehall SG (1961) Universal tire testing machine. In: Proc international technical congress FISITA, Institution of Mechanical Engineers, UK, p 117

    Google Scholar 

  2. Stewart D (1965) A platform with six degrees of freedom. Proc Inst Mech Eng 180:371–386

    Article  Google Scholar 

  3. Wang J, Gosselin CM (1998) Kinematic analysis of singularity loci of spatial four-degree-of-freedom parallel mechanisms using a vector formulation. J Mech Des 120(4):555–558

    Article  Google Scholar 

  4. Dai JS, Kerr DR (2000) Six-component contact force measurement device based on the Stewart platform. J Mech Eng Sci 214(5):687–697

    Article  Google Scholar 

  5. Tsai LW (2000) Solving the inverse dynamics of a Stewart-Gough mechanism by the principle of virtual work. J Mech Des 122(1):3–9

    Article  Google Scholar 

  6. Gosselin CM, Angeles J (1990) Singularity analysis of closed-loop kinematic chains. IEEE Trans Robot Autom 6(3):281–290

    Article  Google Scholar 

  7. Kumar V (1992) Characterization of workspaces of parallel mechanisms. J Mech Des 114(3):368–375

    Article  Google Scholar 

  8. Rico JM, Aguilera LD, Gallardo J, Rodríguez R, Orozco H, Barrera JM (2006) A more general mobility criterion for parallel platforms. J Mech Des 128(1):207–219

    Article  Google Scholar 

  9. Shai O, Pennock GR (2006) Extension of graph theory to the duality between static systems and mechanisms. J Mech Des 128(1):179–191

    Google Scholar 

  10. Dai JS, Sodhi C, Kerr DR (1994) Design and analysis of a new six-component force transducer based on the Stewart platform for robotic grasping. In: Proc the second Biennial European joint conference on engineering systems design and analysis, ASME PD 64(8-3), London, UK, pp 809–817

    Google Scholar 

  11. Mohamed MG, Duffy J (1985) A direct determination of the instantaneous kinematics of fully parallel robot mechanisms. J Mech Transm Autom Des 107(2):226–229

    Article  Google Scholar 

  12. Hunt KH (1983) Structural kinematics of in-parallel-actuated robot-arms. J Mech Transm Autom Des 105(4):705–712

    Article  Google Scholar 

  13. Waldron KJ, Raghavan M, Roth B (1989) Kinematics of a hybrid series-parallel manipulation system. J Dyn Syst Meas Control 111(2):211–221

    Article  Google Scholar 

  14. Clavel R (1988) DELTA, a fast robot with parallel geometry. In: 18th international symposium on industrial robots, Lausanne, France, April 26–28, pp 91–100

    Google Scholar 

  15. Callegari M, Tarantini M (2003) Kinematic analysis of a novel translational platform. J Mech Des 125(2):308–315

    Article  Google Scholar 

  16. Kong X, Gosselin CM (2004) Type synthesis of 3-DOF spherical parallel mechanisms. Int J Robot Res 23(3):237–245

    Article  Google Scholar 

  17. Fang Y, Tsai LW (2004) Structure synthesis of a class of 3-DOF rotational parallel mechanisms. IEEE Trans Robot Autom 20(1):117–121

    Article  Google Scholar 

  18. Bi ZM, Lang SYT (2006) Forward kinematic solution and its applications for a 3-DOF parallel kinematic machine (PKM) with a passive link. Robotica 24(5):549–555

    Article  Google Scholar 

  19. Rodriguez-Leal E, Dai JS (2007) From origami to a new class of centralized 3-DOF parallel mechanisms. In: Proc ASME international design engineering technical conferences & computers and information in engineering conference, September 4–7, Las Vegas, Nevada

    Google Scholar 

  20. Saglia JA, Dai JS, Caldwell DG (2008) Geometry and kinematic analysis of a redundantly actuated parallel mechanism that eliminates singularities and improves dexterity. ASME J Mech Des 130(12):124501

    Article  Google Scholar 

  21. Hunt KH (1982) Structural kinematics of in-parallel actuated robot-arms. In: Proc ASME design and production engineering technical conference, Washington, DC, Sept 12–15, p 9

    Google Scholar 

  22. Zhao TS, Dai JS, Huang Z (2002) Geometric analysis of overconstrained parallel manipulators with three and four degrees of freedom. JSME Int J Ser C Mech Syst Mach Elem Manuf 45(3):730–740

    Google Scholar 

  23. Rodriguez-Leal E, Dai JS, Pennock GR (2008) Kinematic analysis of a new family of centralized parallel mechanisms. In: Proc second international workshop on fundamental issues and future research directions for parallel mechanisms and manipulators, Montpellier, France, September 21 and 22, pp 57–65

    Google Scholar 

  24. Marble SD, Pennock GR (2000) Algebraic-geometric properties of the coupler curves of the RCCC spatial four-bar mechanism. Mech Mach Theory 35(5):675–693

    Article  MATH  MathSciNet  Google Scholar 

  25. Bennett GT (1903) A new mechanism. Engineering 76:777–778

    Google Scholar 

  26. Baker JE (1988) The Bennett linkage and its associated quadric surfaces. Mech Mach Theory 23(2):147–156

    Article  ADS  Google Scholar 

  27. Davidson JK, Hunt KH (2004) Robots and screw theory: applications of kinematics and statics to robotics. Oxford Science Publications, Oxford

    MATH  Google Scholar 

  28. Dai JS, Huang Z, Lipkin H (2006) Mobility of overconstrained parallel mechanisms. J Mech Des 128(1):220–229

    Article  Google Scholar 

  29. Merlet JP (2000) Parallel robots. Kluwer Academic, Dordrecht

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechatronics and Automation, Tecnológico de Monterrey, Monterrey, 64849, Mexico

    Ernesto Rodriguez-Leal

  2. Department of Mechanical Engineering, King’s College London, University of London, Strand, London, WC2R 2LS, UK

    Jian S. Dai

  3. School of Mechanical Engineering, Purdue University, West Lafayette, IN, 47907, USA

    Gordon R. Pennock

Authors
  1. Ernesto Rodriguez-Leal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian S. Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gordon R. Pennock
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian S. Dai.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rodriguez-Leal, E., Dai, J.S. & Pennock, G.R. Kinematic analysis of a 5-R SP parallel mechanism with centralized motion. Meccanica 46, 221–237 (2011). https://doi.org/10.1007/s11012-010-9412-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-010-9412-y

Keywords

Search

Navigation