Dynamic analysis of functionally graded plates using the hybrid Fourier-Laplace transform under thermomechanical loading

Abstract

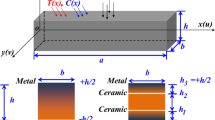
In this study, the analytical solution is presented for dynamic response of a simply supported functionally graded rectangular plate subjected to a lateral thermomechanical loading. The first-order and third-order shear deformation theories and the hybrid Fourier-Laplace transform method are used. The material properties of the plate, except Poisson’s ratio, are assumed to be graded in the thickness direction according to a power-law distribution in terms of the volume fractions of the constituents. The plate is subjected to a heat flux on the bottom surface and convection on the upper surface. A third-order polynomial temperature profile is considered across the plate thickness with unknown constants. The constants are obtained by substituting the profile into the energy equation and applying the Galerkin method. The obtained temperature profile is considered along with the equations of motion. The governing partial differential equations are solved using the finite Fourier transformation method. Using the Laplace transform, the unknown variables are obtained in the Laplace domain. Applying the analytical Laplace inverse method, the solution in the time domain is derived. The computed results for static, free vibration, and dynamic problems are presented for different power law indices for a plate with simply supported boundary conditions. The results are validated with the known data reported in the literature. Furthermore, the results calculated by the analytical Laplace inversion method are compared with those obtained by the numerical Newmark method.