Abstract
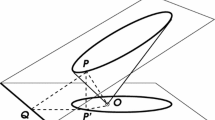
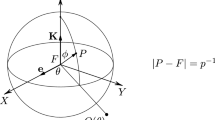
By reconsidering anew our unitary S-description of the family of Kepler conic sections, we show how the plane sum vector S unravels at the core the existence of a constant vector N, which not only discloses in a natural way the cone structure in R 3 which defines the Kepler conic sections, but also enlightens the peculiar genesis of the map devised by Levi-Civita for the regularization of the Kepler problem at collision.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Condurache D, Martinusi V (2007) A complete closed form vectorial solution to the Kepler problem. Meccanica 42:465–476
Deprit A, Elipe A, Ferrer S (1994) Linearization: Laplace vs Stiefel. Celest Mech Dyn Astron 58:151–201
Levi-Civita T (1973) Opere Matematiche, vol 6. Zanichelli, Bologna, pp 111–133
Stiefel EL, Scheifele G (1971) Linear and regular celestial mechanics. Springer, Berlin
Vivarelli MD (1994) The Kepler problem: a unifying view. Celest Mech Dyn Astron 60:291–305
Vivarelli MD (2000) The sum vector S and the fictitious time s in the Kepler problem. Meccanica 35:55–67
Vivarelli MD (2005) The amazing S-code of the conic sections and the Kepler problem. Polipress, Milano
Vivarelli MD (2007) A Julia set for the Kepler problem. Meccanica 42:365–374
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vivarelli, M.D. The Kepler problem: a concealed vector. Meccanica 45, 331–340 (2010). https://doi.org/10.1007/s11012-009-9255-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-009-9255-6