Skip to main content
SpringerLink
Log in

Mathematic modeling and characteristic analysis for dynamic system with asymmetrical hysteresis in vibratory compaction

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

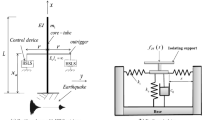
We investigate dynamic characteristics of vibratory compaction system with asymmetrical hysteresis. An asymmetrical model derived from Bouc-Wen differential equation is employed to describe hysteretic behavior of vibration engineering. A practical polynomial expression for hysteretic restoring force is deduced to be substituted into standard equation of the system, assuming that the non-linearity of the restoring force is weak. An asymptotic method, which combines Krylov-Bogolyubov-Mitropolsky (KBM) method with harmonic balance (HB) method, is applied to analyze steady-state responses of the asymmetrical hysteretic system subjected to harmonic excitation. Dynamic responses, such as the restoring force time histories and frequency responses of the system for the first order approximate, are obtained. Furthermore, numerical solution obtained using Runge-Kutta method as well as results of experiments (asphalt compaction on the Beijing-Fuzhou highway) are compared with the asymptotic solution. These results investigated that asymmetrical hysteretic model and the methods applied in this paper are quite appropriate for engineering applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Riedler M, Leitner H, Prillhofer B, Winter G, Eichlseder W (2007) Lifetime simulation of thermo-mechanically loaded components. Meccanica 42:47–59

    Article  MATH  Google Scholar 

  2. Sorokin SV, Terentiev AV, Karihaloo BL (1999) Nonlinear dynamics and stability of a two D.O.F. elastic/elasto-plastic model system. Meccanica 34:311–336

    Article  MATH  Google Scholar 

  3. Ayoub A (2007) Seismic analysis of wood building structures. Eng Struct 29:213–223

    Article  Google Scholar 

  4. Viallet E, Bolsee G, Ladouceur B, Goubin T, Rigaudeau J (2003) Validation of PWR core seismic models with shaking table tests on interacting scale 1 fuel assemblies. In: Transactions of 17th international conference on structural mechanics in reactor technology (SMiRT 17), Prague, Czech Republic, 17–22 August 2003, pp 1–8

  5. Hong SR, Choi SB, Choi YT, Wereley NM (2005) A hydro-mechanical model for hysteretic damping force prediction of ER damper: experimental verification. J Sound Vib 285:1180–1188

    Article  ADS  Google Scholar 

  6. Caughey TK (1960) Sinusoidal excitation of a system with bilinear hysteresis. J Appl Mech (Trans ASME) 27:640–643

    MathSciNet  Google Scholar 

  7. Iwan WD, Furuike DM (1973) The transient and steady-state response of a hereditary system. Int J Non-Linear Mech 8:395–406

    Article  MATH  Google Scholar 

  8. Zhang YF, Iwan WD (2003) Some observations on two piecewise-linear dynamic systems with induced hysteretic damping. Int J Non-Linear Mech 38:753–765

    Article  MATH  MathSciNet  Google Scholar 

  9. Aoki S, Watanabe T (2004) Practical response analysis of a mass-spring impact system with hysteresis damping. Nucl Eng Des 234:1–9

    Article  Google Scholar 

  10. Capecchi D, Vestroni F (1986) Steady-state dynamic analysis of hysteretic systems. J Eng Mech 111:1515–1531

    Article  Google Scholar 

  11. Jin JD, Zhang YF, Wei W (2006) Steady-state response of a binon-linear hysteretic system. Int J Non-Linear Mech 41:926–935

    Article  MATH  Google Scholar 

  12. Bouc R (1967) Forced vibrations of a mechanical system with hysteresis. In: Proceedings of the 4th conference on non-linear oscillation, Prague, Czechoslovakia, 5–9 September 1967, p 315

  13. Wen YK (1976) Method for random vibration of hysteretic systems. J Eng Mech 102:249–263

    Google Scholar 

  14. Chang SI (2004) Bifurcation analysis of a non-linear hysteretic oscillator under harmonic excitation. J Sound Vib 276:215–225

    Article  ADS  Google Scholar 

  15. Awrejcewicz J, Dzyubak LP (2005) Influence of hysteretic dissipation on chaotic responses. J Sound Vib 284:513–519

    Article  ADS  MathSciNet  Google Scholar 

  16. Wong CW, Ni YQ, Lau SL (1994) Steady-state oscillation of hysteretic differential model, I: response analysis. J Eng Mech 120:2271–2297

    Article  Google Scholar 

  17. Wong CW, Ni YQ, Ko JM (1994) Steady-state oscillation of hysteretic differential model, II: performance analysis. J Eng Mech 120:2299–2325

    Article  Google Scholar 

  18. Noori M, Dimentberg M, Hou Z, Christodoulidou R, Alexandrou A (1995) First-passage study and stationary response analysis of a BWB hysteresis model using quasi-conservative stochastic averaging method. Probab Eng Mech 10:161–170

    Article  Google Scholar 

  19. Grabe J (1993) Continuous inverse calculation of soil stiffness from the dynamic behavior of a driving vibratory roller. Arch Appl Mech 63:472–478

    Google Scholar 

  20. Mooney MA, Gorman PB, Gonzalez JN (2005) Vibration-based health monitoring of earth structures. Struct Health Monit 4:137–152

    Article  Google Scholar 

  21. Yoo TS, Selig ET (1979) Dynamics of vibratory-roller compaction. J Geotech Geoenviron Eng 105:1211–1231

    Google Scholar 

  22. Pietzsch D, Poppy W (1992) Simulation of soil compaction with vibratory rollers. J Terramech 29:585–597

    Article  Google Scholar 

  23. Okuizumi N, Kimura K (2004) Multiple time scale analysis of hysteretic systems subjected to harmonic excitation. J Sound Vib 272:675–701

    Article  ADS  Google Scholar 

  24. Worden K, Tomlinson GR (2001) Nonlinearity in structural dynamics: detection, identification. Institute of Physics Publishing, Bristol

    Google Scholar 

  25. Han QK, Wen BC (1998) Analysis of a forced vibration system with asymmetrical hysteresis. J Vib Eng 11:291–297

    Google Scholar 

  26. Li HG, Meng G (2007) Nonlinear dynamics of a SDOF oscillator with Bouc-Wen hysteresis. Chaos Solitons Fractals 34:337–343

    Article  MATH  Google Scholar 

  27. Liu CS, Huang ZM (2004) The steady state responses of s.d.o.f. viscous elasto-plastic oscillator under sinusoidal loadings. J Sound Vib 273:149–173

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350002, People’s Republic of China

    Pei-Hui Shen & Shu-Wen Lin

Authors
  1. Pei-Hui Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shu-Wen Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pei-Hui Shen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shen, PH., Lin, SW. Mathematic modeling and characteristic analysis for dynamic system with asymmetrical hysteresis in vibratory compaction. Meccanica 43, 505–515 (2008). https://doi.org/10.1007/s11012-008-9114-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-008-9114-x

Keywords

Search

Navigation