Skip to main content
SpringerLink
Log in

Start-up Flow of a Bingham Fluid in a Pipe

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

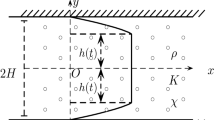
We present an analytical solution of axisymmetric motion for a Bingham fluid initially at rest subjected to a constant pressure gradient applied suddenly. Using the Laplace transform, we obtain expressions which allow the calculation of the instantaneous velocity, plug radius and rate of flow as a function of time. We also give a relation for the shear stress in the plug and in the region where the behaviour of the fluid is Newtonian.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R.K. Duggins (1972) ArticleTitle‘The commencement of flow of a Bingham plastic fluid’ Chem. Eng. Sci 27 1991–1996

    Google Scholar 

  2. A.K. Mitra (1984) ArticleTitle‘Impulsively started flow of a Bingham plastic in a tube’ ASME FED 15 23–25

    Google Scholar 

  3. K.J. Hammad (1998) ArticleTitle‘Unsteady pipe flows of a viscoplastic non-Newtonian fluid: effects of pressure gradient waveform’ ASME FED 247 197–204

    Google Scholar 

  4. K.J. Hammad G.C. Vradis (1996) ArticleTitle‘Pulsatile flows of a Bingham plastic in circular pipes’ ASME FED 237 685–690

    Google Scholar 

  5. D.P. Ly D. Bellet (1976) ArticleTitle‘The study of time-dependent pipe flows of inelastic non-Newtonian fluids using a multiviscous approximation’ J. Non-Newtonian Fluid Mech 1 287–304

    Google Scholar 

  6. M. Nakamura T. Sawada (1987) ArticleTitle‘Numerical Study on the laminar pulsatile flow of slurries’ J. Non-Newtonian Fluid Mech 22 191–206

    Google Scholar 

  7. R. Glowinski (1974) ArticleTitle‘Sur L’écoulement d’un fluide de Bingham dans une conduite cylindrique’ J. de Méc. 13 601–621

    Google Scholar 

  8. R.R. Huilgol B. Mena (2000) ArticleTitle‘On the time estimate for start-up of pipe flows in a Bingham fluid – a proof of the result due to Glowinski, Lions and Trémolière’ J. Non-Newtonian Fluid Mech 94 113–118

    Google Scholar 

  9. Daprà I., Scarpi G., ‘Start-up of a channel-flow of a Bingham fluid initially at rest’. Rend. Mat. Acc. Lincei, 9 (15) (2004).

  10. R.B. Bird G.C. Dai B.J. Yarusso (1983) ArticleTitle‘The Rheology and flow of viscoplastic materials’ Rev. Chem. Eng 1 1–70

    Google Scholar 

  11. M. Abramowitz I.A.. Stegun (1965) Handbook of Mathematical Functions Dover New York

    Google Scholar 

  12. R.G. Brown J.W. Nilsson (1962) Introduction to Linear System Analysis Wiley New York

    Google Scholar 

  13. Safronchik A.I., ‘Non-steady Flow of a visco-plastic Material between parallel Walls’. PMM 23(5) (1959) 925–935. J. Appl. Math. Mech. 23 (1959) 1314–1327.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. DISTART – University of Bologna, Via Risorgimento 2, 40136, Bologna, Italy

    I. Daprà & G. Scarpi

Authors
  1. I. Daprà
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. Scarpi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. Daprà.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Daprà, I., Scarpi, G. Start-up Flow of a Bingham Fluid in a Pipe. Meccanica 40, 49–63 (2005). https://doi.org/10.1007/s11012-004-4997-7

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-004-4997-7

Keywords

Search

Navigation