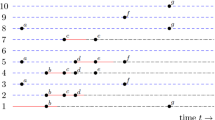
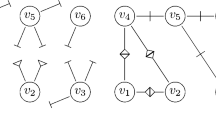
Abstract
This paper is concerned with exact results for the final outcome of stochastic SIR (susceptible \(\rightarrow \) infective \(\rightarrow \) recovered) epidemics among a closed, finite and homogeneously mixing population. The factorial moments of the number of initial susceptibles who ultimately avoid infection by such an epidemic are shown to be intimately related to the concept of a susceptibility set. This connection leads to simple, probabilistically illuminating proofs of exact results concerning the total size and severity of collective Reed–Frost epidemic processes, in terms of Gontcharoff polynomials, first obtained in a series of papers by Claude Lefèvre and Philippe Picard. The proofs extend easily to include general final state random variables defined on SIR epidemics, and also to multitype epidemics.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Addy CL, Longini IM, Haber M (1991) A generalized stochastic model for the analysis of infectious disease final size data. Biometrics 47:961–974
Asmussen S (1987) Applied probability and queues. Wiley, New York
Bailey NTJ (1975) The mathematical theory of infectious diseases and its applications, 2nd edn. Griffin, London
Ball FG (1983) A threshold theorem for the Reed–Frost chain–binomial epidemic. J Appl Prob 20:153–157
Ball FG (1986) A unified approach to the distribution of total size and total area under the trajectory of infectives in epidemic models. Adv Appl Prob 18:289–310
Ball FG, Neal PJ (2002) A general model for stochastic SIR epidemics with two levels of mixing. Math Biosci 180:73–102
Ball FG, O’Neill PD (1999) The distribution of general final state random variables for stochastic epidemic models. J Appl Prob 36:473–491
Ball FG, Mollison D, Scalia-Tomba G (1997) Epidemics with two levels of mixing. Ann Appl Prob 7:46–89
Barbour AD, Mollison D (1990) Epidemics and random graphs. In: Gabriel J-P, Lefèvre C, Picard P (eds) Stochastic processes in epidemic theory. lecture notes in biomathematics, vol 86. Springer, Heidelberg, pp 86–89
Downton F (1968) The ultimate size of carrier-borne epidemics. Biometrika 59:277–289
Gani J, Shanbhag DN (1974) An extension of Raikov’s theorem derivable from a result in epidemic theory. Z Wahrsch Verw Gebiete 29:33–37
Gertsbakh IB (1977) Epidemic processes on a random graph: some preliminary results. J Appl Prob 14:427–438
Gontcharoff W (1937) Détermination des Fonctions Entières par Interpolation. Hermann, Paris
Jaworski J (1999) Epidemic processes on digraphs of random mappings. J Appl Prob 36:780–798
Lefèvre C (1990) Stochastic epidemic models for SIR infectious diseases: a brief survey of the recent general theory. In: Gabriel J-P, Lefèvre C, Picard P (eds) Stochastic processes in epidemic theory. Lecture notes in biomathematics, vol 86. Springer, Heidelberg, pp 1–12
Lefèvre C, Picard P (1990) A non-standard family of polynomials and the final size distribution of Reed–Frost epidemic processes. Adv Appl Prob 22:25–48
Lefèvre C, Picard P (1995) Collective epidemic processes: a general modelling approach to the final outcome of SIR infectious diseases. In: Mollison D (ed) Epidemic models: their structure and relation to data. Cambridge University Press, pp 53–70
Lefèvre C, Picard P (2005) Nonstationarity and randomization in the Reed–Frost epidemic model. J Appl Prob 42:950–963
Ludwig D (1975) Final size distributions for epidemics. Math Biosci 23:33–46
Martin-Löf (1986) Symmetric sampling procedures, general epidemic processes and their threshold limit theorems. J Appl Prob 23:265–282
Pellis L, Ferguson NM, Fraser C (2008) The relationship between real-time and discrete-time generation models of epidemic spread. Math Biosci 216:63–70
Pettigrew HM, Weiss GH (1967) Epidemics with carriers: the large population approximation. J Appl Prob 4:257–263
Picard P, Lefèvre C (1990) A unified analysis of the final size and severity distribution in collective Reed–Frost epidemic processes. Adv Appl Prob 22:269–294
Sellke T (1983) On the asymptotic distribution of the size of a stochastic epidemic. J Appl Prob 20:390–394
Whittle P (1955) The outcome of a stochastic epidemic—a note on Bailey’s paper. Biometrika 42:116–122
Acknowledgements
I am grateful to Karen Guy for helpful discussions. This work was supported by the Engineering and Physical Sciences Research Council [grant number GR/L56282], providing partial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ball, F. Susceptibility Sets and the Final Outcome of Collective Reed–Frost Epidemics. Methodol Comput Appl Probab 21, 401–421 (2019). https://doi.org/10.1007/s11009-018-9631-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11009-018-9631-6
Keywords
- Total size
- Severity
- Susceptibility set
- Symmetric sampling procedure
- Gontcharoff polynomial
- General final state random variables