Abstract
Notwithstanding its complexity in terms of numerical implementation and limitations in coping with problems involving extreme deformation, the finite element method (FEM) offers the advantage of solving complicated mathematical problems with diverse boundary conditions. Recently, a version of the particle finite element method (PFEM) was proposed for analyzing large-deformation problems. In this version of the PFEM, the finite element formulation, which was recast as a standard optimization problem and resolved efficiently using advanced optimization engines, was adopted for incremental analysis whilst the idea of particle approaches was employed to tackle mesh issues resulting from the large deformations. In this paper, the numerical implementation of this version of PFEM is detailed, revealing some key numerical aspects that are distinct from the conventional FEM, such as the solution strategy, imposition of displacement boundary conditions, and treatment of contacts. Additionally, the correctness and robustness of this version of PFEM in conducting failure and post-failure analyses of landslides are demonstrated via a stability analysis of a typical slope and a case study on the 2008 Tangjiashan landslide, China. Comparative studies between the results of the PFEM simulations and available data are performed qualitatively as well as quantitatively.
Similar content being viewed by others
1 Introduction
As a widely found geophysical phenomenon, the term “landslide” refers to various mass movements on slopes, including rockfalls, topples, debris flows, etc. (Varnes 1978). The entire process of a landslide event contains three stages, namely initiation, motion, and deposition. It is common to study the initiation stage by means of various forms of stability analysis, while the motion and deposition stages are considered by means of approaches capable of addressing extreme material deformation.
Based on either solid or fluid mechanics, numerous efforts have been devoted to the investigation of complicated landslide behavior at different stages. Typical numerical approaches for analyzing the initiation of landslides include, but are not limited to, the limit equilibrium method (Fredlund and Krahn 1977), limit analysis method (Chen 1975), and finite element method (Dawson et al. 1999). Among these, use of the FEM, with its flexibility in handling complex geometries, sophisticated constitutive models, various loading conditions, and provision of the time evolution information of the slope body, is prevalent for slope stability analysis. For the motion and deposition stages, the sliding mass is commonly represented by Lagrangian block models (Hungr 1995; Tinti et al. 1997) or flow models (Iverson 1997; Savage and Hutter 1989) based on depth-averaged variables, which are solved numerically using finite-difference schemes (Tai et al. 2002), or by smoothed particle hydrodynamics (SPH) approaches (Pastor et al. 2009). Other approaches capable of modeling the post-failure processes include the discrete element method (Staron 2008), material point method (Llano-Serna et al. 2016), coupled Eulerian–Lagrangian method (Crosta et al. 2003), etc. Notably, although the traditional Lagrangian FEM performs well for slope stability analysis, it cannot capture the motion and deposition stages, since severe mesh distortion is encountered when the sliding mass experiences large changes in geometry. To tackle this issue, the particle finite element method (PFEM), which combines standard finite element analysis and a particle-based technique, was proposed by Idelsohn et al. (2004). Although originally developed to consider fluid–solid interaction problems with free surfaces in fluid mechanics, the PFEM has demonstrated its capability to model the motion and deposition stages of landslides due to the works by Cremonesi et al. (2011), Oñate et al. (2011), and Zhang et al. (2015). Moreover, since the FEM is utilized in the PFEM for each incremental analysis, slope stability analysis can also be performed in the framework of the PFEM, implying an ability to model the entire landslide process, from its initiation through the sliding process to the deposition, in a single simulation.
According to the solution scheme, the versions of the PFEM developed for landslide modeling can be classified into two categories. The PFEM developed by Oñate et al. (2004) and by Cremonesi et al. (2010) belongs to the first category that solves the resulting nonlinear finite element equations using a nested scheme based on Newton’s scheme or a variant thereof. In this solution scheme, iterations are carried out between the level of global structures (where the unbalanced force is minimized) and the level of material points such as the stress integration points (where the stress–strain relationship is fulfilled). This is also the most widely used scheme for the implementation of the FEM in both in-house and commercial numerical packages. In the second category (optimization-based PFEM), the FEM formulation is resolved in mathematical programming. Specifically, the boundary-value problem for landslide analyses is converted into an equivalent optimization problem, for instance a second-order cone programming (SOCP) problem, which is then solved by using the interior point method (IPM). This version of the PFEM inherits some unique merits of the SOCP-FEM, such as natural treatment of the singularities in the Mohr–Coulomb and Drucker–Prager yield criteria and robust extension to handling of multisurface plasticity. One more noticeable advantage of this solution scheme, which is vital to landslide modeling, is its admirable convergence properties. Due to its variational nature, the existence, uniqueness, sensitivity, and stability of the solution can be analyzed mathematically. Indeed, efforts have been devoted to the analysis of the convergence properties of the utilized IPM for solving nonlinear optimization problems; For example, the global and local convergence properties of the IPM for nonlinear programming were demonstrated by Tits et al. (2003), while its stability and convergence rates were analyzed mathematically by Alizadeh et al. (1998). Recently, the possibility of using the optimization-based PFEM for simulating challenging landslide problems has been explored through modeling a flow-like landslide (Zhang et al. 2015), progressive failure of landslides in sensitive clays (Zhang et al. 2017), as well as submarine landslides and their consequences such as induced tsunamis and the impact on ocean pipelines (Zhang et al. 2019).
Notwithstanding its powerful capability, few contributions have been published regarding the implementation of the optimization-based PFEM. Indeed, the theory of the optimization-based PFEM has been well documented and verified by Zhang et al. (2013). However, its numerical implementation, which is widely different from the version of PFEM based on Newton’s iteration schemes, has not been introduced in detail, which therefore handicaps its further applications. We remark that the solution scheme for the finite element formulation in the optimization-based PFEM differs considerably from that in the version developed by Oñate et al. (2004) and Cremonesi et al. (2010). Additionally, we note that, although the capability of the optimization-based PFEM for landslide modeling has already been explored, there are only a few efforts devoted to studies comparing the optimization-based PFEM versus the common approaches for landslide modeling in geosciences (e.g., versus depth-averaged approaches). This work aims to contribute to fill these gaps with a twofold objective: (1) to detail the numerical implementation of the optimization-based PFEM to assist researchers from geoscience in developing their own version, and (2) to provide a quantitative comparison between the optimization-based PFEM and the techniques commonly adopted in geosciences to treat landslides, including both stability analysis and post-failure analysis.
2 Governing Equations
In this section, the governing equations for quasistatic and dynamic analyses of rate-independent elastoplastic problems under plane-strain conditions are summarized. The equations consist of the equilibrium equation, strain–displacement relation, constitutive equation, and boundary conditions. Additionally, the contact between the deformable solid (e.g., sliding mass) and rigid surface (e.g., basal surface) is also considered in the formulation. For the dynamic analysis, the θ time-integration method (Bathe and Wilson 1973) is used to discretize the governing equations in the time domain.
2.1 Static Analysis
For a two-dimensional (2D) domain V, delimited by a boundary S, the set of governing equations for a static analysis is as follows:
-
(a)
The equilibrium equation
$$ \nabla^{\text{T}}\varvec{\sigma}+ \varvec{b} = 0,\quad {\text{in}}\;V, $$(2.1)where the operator is \( \nabla^{\text{T}} = \left( {\frac{\partial }{\partial x}, 0, \frac{\partial }{\partial y}; 0, \frac{\partial }{\partial y}, \frac{\partial }{\partial x}} \right) \), the body force is \( \varvec{b} = \left( {b_{x} , b_{y} } \right)^{\text{T}} \), and the stress is \( \varvec{\sigma}= \left( {\sigma_{xx} ,\sigma_{yy} ,\sigma_{xy} } \right)^{\text{T}} \).
-
(b)
The strain–displacement relationship
$$ \varvec{\varepsilon}= \nabla \varvec{u}, $$(2.2)where the strain is \( \varvec{\varepsilon}= \left( {\varepsilon_{xx} , \varepsilon_{yy} ,2\varepsilon_{xy} } \right)^{\text{T}} \) and the displacement is \( \varvec{u} = \left( {u_{x} , u_{y} } \right)^{\text{T}} \).
-
(c)
The boundary conditions on S
$$ \varvec{N\sigma } = \varvec{t} $$(2.3a)$$ \varvec{u} = \varvec{u}^{\rm p}, $$(2.3b)where \( \varvec{N} = \left( {n_{x} , 0, n_{y} ;0, n_{y} , n_{x} } \right) \), t is the traction force, and \( \varvec{u}^{\rm p} \) is the prescribed displacement.
-
(d)
The constitutive relationship
$$ F\left(\varvec{\sigma}\right) \le 0 $$(2.4a)$$ \varvec{\varepsilon}=\varvec{\varepsilon}^{\rm e} +\varvec{\varepsilon}^{\rm p} ,\;\varvec{\varepsilon}^{\rm e} = {\mathbb{C}}\varvec{\sigma},\;\varvec{\varepsilon}^{\rm p} = \lambda \nabla_{G} G\left(\varvec{\sigma}\right), $$(2.4b)in which F is the yield function, \( \varvec{\varepsilon}^{\rm e} \) and \( \varvec{\varepsilon}^{\rm p} \) are the elastic and plastic strains, respectively, \( {\mathbb{C}} \) is the elastic compliance matrix, λ is the plastic multiplier, and G is the plastic potential. As shown in Eq. (2.4b), the additive decomposition of the strain is used, whose incremental form is
$$ \Delta\varvec{\varepsilon}= {\mathbb{C}}\Delta\varvec{\sigma}+ {\Delta }\lambda \nabla_{G} G\left(\varvec{\sigma}\right). $$(2.5)
For an associated flow rule, we have \( G = F \). When the material undergoes purely elastic deformation, the plastic multiplier increment \( \Delta \lambda = 0 \) and \( F\left(\varvec{\sigma}\right) < 0 \), whereas when the material yields, we have \( \Delta \lambda > 0 \) and \( F\left(\varvec{\sigma}\right) = 0 \). This constraint is the so-called complementary condition that
which implies that the incremental form of the constitutive relationship is as follows
2.2 Dynamic Analysis
For dynamic analyses, the inertial force should be included in the equilibrium Eq. (2.1), that is
By means of the θ-method (Bathe and Wilson 1973), the stresses and velocities can be rewritten as \( \varvec{\sigma}= \theta_{1}\varvec{\sigma}_{n + 1} + \left( {1 - \theta_{1} } \right)\varvec{\sigma}_{n} \) and \( \varvec{v} = \theta_{2} \varvec{v}_{n + 1} + \left( {1 - \theta_{2} } \right)\varvec{v}_{n} \), rendering Eq. (2.8a, b) as
Hereafter, the subscripts n and n + 1 denote the known and unknown states, and Δt is the time increment. By introducing a new intermediate variable, i.e., the inertial force \( \varvec{\gamma} \), whose definition is shown in Eq. (2.12), and substituting Eq. (2.9b) into Eq. (2.9a), the latter can be rearranged as
and the according traction boundary condition Eq. (2.3a) becomes
in which
Equation (2.9b) can also be rearranged as
which is used to update the velocity vn+1 after the displacement increment \( \Delta \varvec{u} \) is obtained. It should be mentioned that the time integration scheme is unconditionally stable when \( \theta_{1} \ge \frac{1}{2} \) and \( \theta_{2} \ge \frac{1}{2} \).
2.3 Contact Analysis
The rigid no-penetration contact scheme is adopted to consider the interaction between the sliding mass and the basal surface, implying that, for any points of the sliding mass, the incremental displacement of the point cannot exceed the gap between the point and the boundary, as illustrated in Fig. 1. Therefore, the corresponding contact conditions are as follows
where n is the outward unit vector of the rigid surface, g0 is the gap between the boundary point of the deformable material and the rigid surface at t = tn, p is the normal force, q is the tangential force, and µ is the friction coefficient.
3 Equivalent Min–Max Program
The aforementioned governing equations can be reformulated as equivalent min–max optimization problems according to the works of Simo et al. (1989), Krabbenhoft et al. (2007), and Zhang et al. (2013), where detailed derivations are documented. In this section, a brief summary is provided for those equivalent min–max optimization problems.
The Hellinger–Reissner variational principle (Reissner 1950) is adopted to reformulate the quasistatic elastoplastic problem. According to Krabbenhoft et al. (2007), the equivalent optimization problem is in the form of
As shown, both the displacement and stress are independent master fields for the above optimization problem. The optimal solution of problem (3.1) is a saddle point that renders neither the maximum nor the minimum of the functional. The incremental form of (3.1) is
which is the one used for the incremental finite element analysis of quasistatic elastoplastic problems.
Efforts have also been devoted to reformulate the governing equations for dynamic elastoplastic problems. It was demonstrated by Zhang et al. (2013) that the min–max optimization problem equivalent to the governing equations discretized by the θ-method for dynamic analysis is
where the inertial force \( \varvec{\gamma} \) is included as an independent master field in the maximum part of the optimization problem. The contact constraints, i.e., (2.14), will be taken into account later.
4 Finite Element Discretization
4.1 Mixed Triangular Element
Using standard finite element notations, the master fields of the min–max program are approximated as follows
where \( \hat{\varvec{\sigma }} \), \( \hat{\varvec{u}} \) and \( \hat{\varvec{\varUpsilon }} \) are the stress, displacement, and inertial force at mesh nodes and \( \varvec{N}_{\sigma } \), \( \varvec{N}_{u} \), and \( \varvec{N}_{\gamma } \) are the matrices consisting of the interpolation shape functions. Specifically, the mixed isoparametric triangular element shown in Fig. 2 is selected in our simulation, where a quadratic shape function is used for the fields of the displacement and inertial force (\( \varvec{N}_{u} = \varvec{N}_{\gamma } \)) whereas a linear shape function is used for the stress field.
Using (4.1), the relationship between strains and nodal displacements is expressed as
The shape functions \( \varvec{N}_{u} \) (or \( \varvec{ N}_{\gamma } \)) and \( \varvec{ N}_{\sigma } \) are
in which ξ, η, and ς are the local coordinates and ς = 1 − ξ − η. The stress interpolation points are located at ((ξ1, η1), (ξ2, η2), (ξ3, η3)) = ((1/6, 1/6), (2/3, 1/6), (1/6, 2/3)).
4.2 Finite Element Discretization
Using the finite element discretization, the discrete form of the min–max problem (3.3) for the dynamic analysis of elastoplastic problems is
where
In the optimization problem (4.4), the yield function (4.4b) is imposed at the stress interpolation points, with nσ and \( \hat{\varvec{\sigma }}_{n + 1}^{j} \) being respectively the total number of stress interpolation points and the stress states at the jth stress integration point at \( t_{n + 1} \). The minimization part of the min–max problem (4.4a) can be resolved analytically, meaning that the min–max problem (4.4) is equivalent to the following maximization problem
which is the one for dynamic elastoplastic analysis.
The optimization problem (4.6) can be degraded to the one for quasistatic elastoplastic analysis by removing the terms relevant to dynamics and setting θ1 = θ2 = 1. Specifically, the discretized optimization problem for quasistatic elastoplastic analysis is
in which \( \varvec{f} = \mathop \int \limits_{V}^{ } \varvec{N}_{u}^{\text{T}} \varvec{b}{\text{d}}V + \mathop \int \limits_{S}^{ } \varvec{N}_{u}^{\text{T}} \varvec{t}{\text{d}}S \).
According to Zhang et al. (2013), further consideration of contact constraints, i.e. (2.14), transforms the optimization problem (4.6) into
in which ρ = (ρx, ρy)T are the nodal contact forces in the global coordinate system relating to the normal and tangential contact forces p and q via n and \( \hat{\varvec{n}} \). n is the unit vector normal to the rigid boundary, and \( \hat{\varvec{n}} = \left( { - n_{2} ,n_{1} } \right)^{\text{T}} \). Assuming that the inclination angle of the slope is θs (Fig. 1), the corresponding components are n1 = sin θs and n2 = cos θs. The logical index set of contact nodes is denoted by Ec, and nc is the total number of potential contact nodes. The potential contact nodes are set as the nodes on the surface S of the computational domain V. The present maximization problem is a type of convex optimization problem that can be recast as a standard second-order cone programming (SOCP) problem and then resolved using the interior point method. For simplicity, the present scheme for the finite element solution is abbreviated as SOCP-FEM.
5 Numerical Implementation
Although the theories of the SOCP-FEM analysis for quasistatic and dynamic elastoplastic problems have been well demonstrated, there are only few efforts devoted to its numerical implementation. This section focuses primarily on the numerical implementation of the SOCP-FEM, with emphasis on some key aspects. In particular, we focus on (1) the implementation of the boundary conditions in the SOCP-FEM, (2) the transformation of the resulting maximization problem for quasistatic/dynamic elastoplastic analyses into a standard SOCP problem, and (3) the solution of the resulting SOCP problem using the IPM available in MOSEK (MOSEK ApS 2019).
5.1 Implementation of Boundary Conditions
The traction and displacement boundary conditions have to be imposed so that the boundary-value problem can be resolved. The traction boundary condition, for instance Eq. (2.3a), is handled by integrating tractions along the boundary surface, resulting in equivalent nodal forces [e.g. Eq. (4.5e)]. In other words, the implementation of the traction boundary condition in the SOCP-FEM is exactly the same as that in the traditional displacement-based FEM (Bathe 2006).
Nevertheless, the imposition of the displacement boundary condition (2.3b) in the SOCP-FEM differs from that in the displacement-based FEM. In the traditional displacement-based FEM, the displacement boundary condition is implemented either by the penalty method or by modifying the global stiffness matrix. In contrast, the SOCP-FEM requires the introduction of a new field variable, i.e., the nodal reaction force \( \hat{\varvec{r}}_{n + 1} \), for this purpose. Specifically, for quasistatic problems, the discretized optimization problem with displacement boundary conditions being fulfilled is in the form of
where Eu, consisting of 0 and 1, is the index matrix to indicate the prescribed displacement \( \hat{\varvec{u}}^{\rm p} \). The underlined terms in the objective function and the equality constraint in problem (5.1) are induced by the displacement boundary conditions. To check its validity, the Lagrangian associated with (5.1) is constructed, which is
Differentiating the Lagrangian with respect to the reaction force \( \hat{\varvec{r}}_{n + 1} \) leads to
which apparently is the displacement boundary condition (2.3b). For dynamic problems, the imposition of displacement boundary conditions is achieved in the same manner.
5.2 Reformulation as a SOCP Problem
The aforementioned optimization problem [i.e. (4.8)] can be reformulated as a standard second-order cone programming (SOCP) problem in the form of
where x = (x1, x2, …, xn)T is the vector of optimization variables, a, b, and c are the matrix and vectors of factors, and \( {\mathcal{K}} \) is a tensor product of second-order cones such that \( {\mathcal{K}} = {\mathcal{K}}_{1} \times \cdots \times {\mathcal{K}}_{l} \). The second-order cones can be of the following types:
-
Quadratic cone
$$ {\mathcal{K}}_{q}^{n} = \left. {\left\{ {\varvec{x} \in \varvec{ }{\mathbb{R}}^{n} : x_{1} \ge \sqrt {x_{2}^{2} + \cdots + x_{n}^{2} } } \right.} \right\} $$(5.5a)
or
-
Rotated quadratic cone
$$ {\mathcal{K}}_{r}^{n} = \left. {\left\{ {\varvec{x} \in \varvec{ }{\mathbb{R}}^{n} : 2x_{1} x_{2} \ge \mathop \sum \limits_{j = 3}^{n} x_{j}^{2} , x_{1} ,x_{2} \ge 0 } \right.} \right\} $$(5.5b)
Specifically, the SOCP problem equivalent to the maximization problem (4.8) is
where \( \varvec{x}_{n + 1} \) is a vector consisting of all the optimization variables [i.e. (5.9)].
Remark 1
The SOCP problem (5.6) is obtained by first converting the quadratic term \( \frac{1}{2}\Delta \hat{\varvec{\sigma }}^{\text{T}} \varvec{C}\Delta \hat{\varvec{\sigma }} \) in the objective function of (4.8) into the minimization of a scalar variable [i.e., variable m in (5.6a)] subject to linear equalities and rotated quadratic constraints [i.e. (5.6c)]. The same operation is applied to the quadratic term \( \frac{1}{2}\Delta t^{2} \hat{\varvec{\gamma }}_{n + 1}^{\text{T}} \varvec{D\hat{\gamma }}_{n + 1}^{ } \) in the objective function, resulting in the variable s in (5.6a) and the constraints in (5.6d). Contact constraints in (4.8d–f) are reformulated as those in (5.6e), in which quadratic constraints are enforced. The yield criterion \( F\left( {\hat{\varvec{\sigma }}_{n + 1}^{j} } \right) \le 0 \) is equivalent to the constraints in (5.6f).
In our simulations, the Mohr–Coulomb criterion is adopted, which in a plane-strain case is
and thus the according χ, H, and d in (5.6f) are
5.3 Solution Using MOSEK
The resulting SOCP problem (5.6) can be resolved using the IPM, which is a robust solution scheme available in MOSEK (MOSEK ApS 2019). In this section, the program submitted to MOSEK for the solution is presented in detail. All information related to the program is stored in an object called “prob” in MOSEK.
Specifically, the optimization variables of the SOCP problem (5.6) are as follows
and the corresponding vectors c and b and the matrix a [see also problem (5.4)] are
Remark 2
The linear equality constraint (5.4b) is implemented as the lower and upper bounds, namely prob·blc ≤ prob·ax ≤ prob·buc.
The inequality constraints in (5.6) are in the form of quadratic or rotated quadratic cones. There are a total of \( n_{c} + n_{\sigma } + 2 \) conic cones according to the expressions in (5.6c–f). Specifying the type of each cone and the index of its members in x, the conic constraints can be defined straightforwardly in “prob.” A detailed solution scheme for the SOCP-FEM analysis is provided in Algorithm 1 for reference.
Algorithm 1. Solution scheme | |
|---|---|
For the ith incremental analysis: | |
1. | Update the status of variables such as the velocity, the acceleration and the stress; |
2. | Form global matrices A, B, C, D, H, d according to (4.5) and (5.8b); |
3. | Calculate \( \tilde{\varvec{f}} \) according to Eq. (2.12) and Eq. (4.5e) |
4. | Contact detection: |
(1) Calculate g0 of potential contact nodes; | |
(2) Update normal vectors in Eqs. (4.8d)–(4.8e) with inclined slope angle θs; | |
5. | Construct the SCOP program based on Eq. (5.10) and submit to MOSEK |
6. | Extract/calculate the status variables: |
For instance: | |
(a) Find stresses \( \hat{\varvec{\sigma }}_{n + 1} \) in res.sol.itr.xx; | |
(b) Calculate velocity \( \hat{\varvec{v}}_{n + 1} \) using Eq. (2.13) with \( \Delta \hat{\varvec{u}} \) obtained from res.sol.itr.y; | |
(c) Calculate the increment of strain tensors using Eq. (2.2) and Eq. (2.5); | |
Return to step 1 with i = i + 1; | |
Remark 3
The optimization solver returns the structure type of the solutions named “res” at the end of each analysis step, and the solutions of x are contained in res.sol.itr.xx. The incremental displacement \( \Delta \hat{\varvec{u}} \) is the dual variable of \( \hat{\varvec{\sigma }}_{n + 1} \) and is stored in res.sol.itr.y.
6 Particle Finite Element Technique
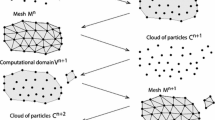
Originating in fluid mechanics, the PFEM has demonstrated its ability to tackle issues such as free surface evolution and mesh distortion. Some challenging fluid mechanics problems that have been solved successfully include, but are not limited to, modeling of free surface flows and their interaction with solid structures, wave breaking, multiphase flows, etc. (Idelsohn et al. 2003, 2004; Oñate et al. 2004, 2008, 2011). The key idea behind the PFEM is the treatment of mesh nodes as free particles that can move and even separate from the computational domain to which they originally belonged. In a given time interval \( \left[ {t_{n} , t_{n + 1} } \right] \), the basic steps of the PFEM are as follows (see also Fig. 3):
-
1.
Erase the mesh topology and update the position of mesh nodes based on the solved incremental displacement to obtain a cloud of particles, \( C_{n + 1} \) (Fig. 3a, b);
-
2.
Use the α-shape method (Edelsbrunner and Mücke 1994) to identify the new computational domain \( \varOmega_{n + 1} \) based on \( C_{n + 1} \) (Fig. 3c);
-
3.
Remesh the domain \( \varOmega_{n + 1} \) to obtain a new mesh \( M_{n + 1} \) (Fig. 3d);
-
4.
Map the history variables from the old mesh \( M_{n} \) to the new mesh \( M_{n + 1} \) using the unique element method introduced by Hu and Randolph (1998);
-
5.
Solve the equations using Algorithm 1 based on the new mesh \( M_{n + 1} \).
It is worth noting that the governing equations used in this version of PFEM are under the assumption of infinitesimal strain. At the end of each incremental analysis, the configuration is updated according to the solved displacement. This assumption may lead to several errors for large-deformation analysis. However, practically, the error induced due to the infinitesimal strain assumption is relatively minor, because the used incremental step is very small. The present version of the PFEM with small-strain theory has been validated against several benchmarks such as the modeling of a water dam break, granular column collapse, underwater granular flows and the related induced waves, and non-Newtonian flows in an annular viscometer by Zhang et al. (2019), where satisfactory agreement between the PFEM simulation results and available experimental data and/or analytical results was obtained. For the PFEM derived from the concepts of large-strain plasticity and its application to granular material flows which are closely related to landslide propagations, we refer the reader to Dávalos et al. (2015).
7 Landslide Modeling
7.1 Stability Analysis
7.1.1 Slope Stability Analysis by SOCP-FEM
Practically, the stability analysis of a slope is carried out using the strength reduction method (SRM) to identify the critical state of the slope by gradually reducing the strength of the soil. The critical state is indicated by the factor of safety (FOS), defined as the ratio of the actual soil shear strength to the minimum shear strength required to prevent failure (Bishop 1955); For example, when the Mohr–Coulomb model is used and the cohesion and internal friction angle are represented by c and φ, then according to the SRM (Dawson et al. 1999), these parameters are reduced by a reduction factor (RF), viz.
The RF is the FOS of the slope when the used \( c^{\prime} \) and \( \tan \varphi ' \) are at the minimum values required to prevent failure. In other words, a slope with a FOS greater than one is identified as stable; otherwise, it is unstable.
To verify the accuracy of the SOCP-FEM approach for slope stability analysis, a homogeneous soil slope that has been analyzed using the limit equilibrium method (LEM) and the finite element method by Cheng et al. (2007) is reexamined in this section. The initial geometry of the example is illustrated in Fig. 4. The density, elastic modulus, and Poisson’s ratio of the soil are 2000 kg/m3, 14 MPa, and 0.3, respectively. Simulations with both the associated (\( \psi = \varphi \)) and nonassociated (\( \psi = 0^\circ \)) flow rules are conducted using SOCP-FEM under quasistatic assumptions with material parameters in line with those in Cheng et al. (2007). For the case of the nonassociated flow rule, the strategy presented in Krabbenhoft et al. (2012) is utilized. A total of 6095 triangular elements are used to discretize the slope in our simulations.
The binary search algorithm illustrated in Fig. 5 is employed to calculate the FOS. The critical failure state of a slope is determined when the optimization solver is not feasible or the maximum incremental displacement is higher than a given threshold. An initial range [RF1 = 0.2, RF2 = 10] is set to trigger the search process, and when the tolerance |RF2 − RF1|/RF1 < 10−3 is achieved, the calculated reduction factor RF1 is the FOS of the slope.
Comparative studies regarding the FOS obtained from our SOCP-FEM analysis, the limit equilibrium method, and the traditional finite element method are presented in Table 1, revealing that satisfactory agreement is achieved, which demonstrates the correctness of the proposed SOCP-FEM for slope stability analysis.
7.1.2 post-failure Analysis by PFEM
In the framework of the PFEM, not only the FOS of a slope can be determined but also the post-failure processes and final runout distances for different reduction factors. This can be achieved through the dynamic analysis shown in Sect. 3.2. To illustrate this capability, case 12 in Table 1 is reanalyzed with the nonassociated flow rule. Four different reduction factors are used, and the corresponding final deposits from the simulations are illustrated in Fig. 6.
Final deposits obtained from PFEM simulation for reduction factor (RF) of a 2.24, b 2.3, c 2.4, and d 2.9. Contours refer to displacement of soils (unit: meters); slip surfaces from the analysis by SRM1, SRM2, and LEM extracted from Cheng et al. (2007)
As displayed, for RF = 2.24 and 2.3, clear sliding surfaces are identified from the PFEM simulation, which coincide with the slip surfaces determined by other approaches (Fig. 6a, b). However, soil elements in these two cases experience very small displacements. This is because these reduction factors are very close to the factor of safety of the slope, implying that the slope will tend to become stable again after limited deformation. For RF = 2.4 (Fig. 6c), the deformation is well identified and a maximum displacement of around 0.7 m is experienced by soil nodes along the slip surface. Further increase of the reduction factor leads to greater deformations; For example, when RF = 2.9, the sliding mass has a moving distance exceeding 2 m, as well predicted by our approach.
7.2 Landslide Propagation
Computing the propagation of landslides requires an accurate description of the rheological behavior of the involved geomaterials. In geoscience, the propagation process of a landslide is usually simulated by solving equations describing the fluid behavior of the sliding mass based on Eulerian approaches. In the present PFEM framework, more sophisticated material constitutive models can be implemented for landslide propagation. It is of interest to compare the simulation results of a real landslide case obtained from the present PFEM method and those from depth-averaged models.
To this end, a historical event, i.e., the Tangjiashan mass failure in Sichuan Province, China, is addressed in this section (Fig. 7). The failure was triggered by the 2008 Wenchuan earthquake, and the sliding mass crashed rapidly into the Jianjiang River, causing a landslide dam with a death toll of up to 84 (Hu et al. 2009; Xu et al. 2009). The slide moved along a complex topography with maximum slope angle of \( 40^{^\circ } \), and the motion lasted around 30 s according to Hu et al. (2009). The data about the landslide body and the deposit are extracted from the field survey conducted by Hu et al. (2009). In our PFEM simulation, the domain is discretized by using 3335 elements, and a time step Δt of 0.1 s is used. According to Huang et al. (2012), the sliding mass can be represented by a Mohr–Coulomb model with the following material parameters: density ρ = 2000 kg/m3, frictional angle φ = \( 30^{^\circ } \), dilation angle ψ = \( 0^{^\circ } \), and cohesion c = 30 kPa. The basal friction coefficient is chosen as μ = 0.27. For the time integration, the backward Euler scheme, i.e., θ1 = θ2 = 1, is used in the PFEM simulation.
In addition to the PFEM, the landslide motion was also simulated by using the depth-averaged model (Xia and Liang 2018). The depth-averaged equations (DAEs) are derived from the Navier–Stokes equations by using the long-wave approximation and the Mohr–Coulomb rheology law (Savage and Hutter 1989) with topography modifications suitable for a global Cartesian coordinate system. The numerical code was developed according to the Nessyahu–Tadmor scheme (Nessyahu and Tadmor 1990; Tai et al. 2002) and has been validated with typical benchmarks and a historical landslide event (Wang et al. 2019). In contrast to the present PFEM model, the adopted depth-averaged model only considers the basal Mohr–Coulomb friction law, ignoring the effects coming from the internal friction angle and the cohesion of the sliding mass. This means that the material parameters required for the depth-averaged analysis consist of the density ρ = 2000 kg/m3 and the frictional coefficient of the basal surface μ = 0.27. In the simulation by the depth-average model, the common used earth pressure coefficient (Savage and Hutter 1989) is assumed to be unity, like in other recent works (e.g., Russell et al. 2019).
The positions of the sliding mass obtained from the PFEM analysis at four different time instants are shown in Fig. 8, where the velocity magnitude contour is depicted and the dashed line represents the profile obtained from the depth-averaged model. At t = 6 s (Fig. 8a), the landslide moves as a whole with velocity of around 20 m/s while the depth-averaged model provides a slightly faster motion. Later, velocity distinctions within the landslide body in the PFEM simulation can be observed when the mass climbs up the opposite side of the mountain (Fig. 8b). Impeded by the antislope, the front of the landslide decelerates rapidly while the rear of the landslide still moves with a velocity greater than 25 m/s (Fig. 8c). The sliding mass stops at t = 24 s in the PFEM simulation, as shown in Fig. 8d, whereas the landslide process lasts longer in the depth-averaged simulation. In particular, the rear sector pushes the front mass and then moves back in the depth-averaged simulation, implying that the sliding mass behaves more like a fluid if the DAEs are used.
Figure 9 compares the topographies from the observational data (Hu et al. 2009) and the simulation by SPH (Huang et al. 2012), the present PFEM, and the DAEs. All simulation results agree well with the observation data. The mass variations (represented by the ratio of the current total mass to the initial mass of the sliding body) of the PFEM simulation are shown in Fig. 9b, where a maximum of 1.5% mass change is observed. It is thus concluded that, although reidentification of computational domains is conducted in the PFEM, mass conservation can still be maintained well. Considering the landslide as a whole, the mean velocity profile of the landslide is shown in Fig. 9c. In the PFEM simulation, the landslide accelerates to around 26 m/s in the first 10 s then decelerates to still. In the depth-averaged simulation, the main mean velocity profile is quite similar, while an additional velocity profile is produced due to the back motion of the landslide body. In general, the present two simulations are nearly consistent in capturing the main motion of the Tangjiashan landslide. Nevertheless, it should be emphasized that the DAEs cannot be used to predict the triggering of the landslide (for example, slope stability analysis) due to its nature, whereas the present optimization-based PFEM is capable of both failure and post-failure predictions.
8 Conclusions
This paper focuses on the numerical implementation of a version of PFEM in which the finite element formulation is transformed into a second-order cone programming (SOCP-FEM), and on its application to failure and post-failure analysis of landslides.
Based on the Hellinger–Reissner variational principle, the finite element formulation for static/dynamic elastoplastic analyses with interactions between deformable bodies and a rigid surface can be cast into equivalent optimization programs and resolved efficiently using available advanced optimization engines. This paper provides a detailed introduction to the numerical implementation of the optimization-based finite element method, particularly the SOCP-FEM. It is shown that the implementation can be achieved straightforwardly by constructing the corresponding matrices, significantly releasing the researcher from programming. The present details can serve as a reference for those who are willing to develop their own code with modifications for application to different geoscience problems.
Meanwhile, the version of PFEM, which is a mixture of the SOCP-FEM and the particle technique, is applied to the modeling of landslides with detailed comparative studies of both failure and post-failure analyses. Associated with the shear strength reduction technique and the binary search algorithm, the method is tested against the stability analysis benchmark published by Cheng et al. (2007). Additionally, it is shown that the present model is capable of simulating both the failure and post-failure stages of the landslide in a single simulation. Moreover, the propagation of the historical event of the 2008 Tangjiashan landslide, China is investigated by the PFEM model and a depth-averaged model (Xia and Liang 2018). Overall, satisfactory agreement is obtained between the results from the PFEM simulation and the depth-averaged modeling, demonstrating the capability of the PFEM for modeling landslide propagation, although the sliding mass behaves more like a fluid according to the depth-averaged simulation results.
References
Alizadeh F, Haeberly J-PA, Overton ML (1998) Primal-dual interior-point methods for semidefinite programming: convergence rates, stability and numerical results. SIAM J Optim 8:746–768
Bathe KJ (2006) Finite element procedures, 2nd edn. Prentice Hall, Pearson Education, Watertown
Bathe KJ, Wilson EL (1973) Stability and accuracy analysis of direct integration methods. Earthq Eng Struct Dyn 1:283–291
Bishop AW (1955) The use of the slip circle in the stability analysis of slopes. Géotechnique 5:7–17
Chen W-F (1975) Limit analysis and soil plasticity. Elsevier, Amsterdam
Cheng YM, Lansivaara T, Wei WB (2007) Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Comput Geotech 34:137–150
Cremonesi M, Frangi A, Perego U (2010) A Lagrangian finite element approach for the analysis of fluid–structure interaction problems. Int J Numer Methods Eng 84:610–630
Cremonesi M, Frangi A, Perego U (2011) A Lagrangian finite element approach for the simulation of water-waves induced by landslides. Comput Struct 89:1086–1093
Crosta GB, Imposimato S, Roddeman DG (2003) Numerical modelling of large landslides stability and runout. Nat Hazards Earth Syst Sci 3:523–538
Dávalos C, Cante J, Hernández JA, Oliver J (2015) On the numerical modeling of granular material flows via the particle finite element method (PFEM). Int J Solids Struct 71:99–125
Dawson EM, Roth WH, Drescher A (1999) Slope stability analysis by strength reduction. Géotechnique 49:835–840
Edelsbrunner H, Mücke EP (1994) Three-dimensional alpha shapes. ACM Trans Graph 13:43–72
Fredlund DG, Krahn J (1977) Comparison of slope stability methods of analysis. Can Geotech J 14:429–439
Hu Y, Randolph MF (1998) A practical numerical approach for large deformation problems in soil. Int J Numer Anal Methods Geomech 22:327–350
Hu X, Huang R, Shi Y, Lu X, Zhu H, Wang X (2009) Analysis of blocking river mechanism of Tangjiashan landslide and dam-breaking mode. Chin J Rock Mech Eng 28:181–189 (in Chinese)
Huang Y, Zhang W, Xu Q, Xie P, Hao L (2012) Run-out analysis of flow-like landslides triggered by the Ms 8.0 2008 Wenchuan earthquake using smoothed particle hydrodynamics. Landslides 9:275–283
Hungr O (1995) A model for the runout analysis of rapid flow slides, debris flows, and avalanches. Can Geotech J 32:610–623
Idelsohn SR, Oñate E, Del Pin F (2003) A Lagrangian meshless finite element method applied to fluid–structure interaction problems. Comput Struct 81:655–671
Idelsohn SR, Oñate E, Del Pin F (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int J Numer Methods Eng 61:964–989
Iverson RM (1997) The physics of debris flow. Rev Geophys 35:245–296
Krabbenhoft K, Lyamin AV, Sloan SW, Wriggers P (2007) An interior-point algorithm for elastoplasticity. Int J Numer Methods Eng 69:592–626
Krabbenhoft K, Karim MR, Lyamin AV, Sloan SW (2012) Associated computational plasticity schemes for nonassociated frictional materials. Int J Numer Methods Eng 90:1089–1117
Llano-Serna MA, Farias MM, Pedroso DM (2016) An assessment of the material point method for modelling large scale run-out processes in landslides. Landslides 13:1057–1066
MOSEK ApS (2019) MOSEK optimization toolbox for MATLAB manual. Release 9.0.84(BETA)
Nessyahu H, Tadmor E (1990) Non-oscillatory central differencing for hyperbolic conservation laws. J Comput Phys 87:408–463
Oñate E, Idelsohn SR, Del Pin F, Aubry R (2004) The particle finite element method—an overview. Int J Comput Methods 1:267–307
Oñate E, Idelsohn SR, Celigueta MA, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid–multibody interaction and bed erosion in free surface flows. Comput Methods Appl Mech Eng 197:1777–1800
Oñate E, Celigueta MA, Idelsohn SR, Salazar F, Suárez B (2011) Possibilities of the particle finite element method for fluid–soil–structure interaction problems. Comput Mech 48:307–318
Pastor M, Haddad B, Sorbino G, Cuomo S, Drempetic V (2009) A depth-integrated, coupled SPH model for flow-like landslides and related phenomena. Int J Numer Anal Methods Geomech 33:143–172
Peng M, Zhang L (2012) Analysis of human risks due to dam break floods-part 2: application to Tangjiashan landslide dam failure. Nat Hazards 64:1899–1923
Reissner E (1950) On a variational theorem in elasticity. J Math Phys 29:90–95
Russell AS, Johnson CG, Edwards AN, Viroulet S, Rocha FM, Gray JMNT (2019) Retrogressive failure of a static granular layer on an inclined plane. J Fluid Mech 869:313–340
Savage SB, Hutter K (1989) The motion of a finite mass of granular material down a rough incline. J Fluid Mech 199:177–215
Simo JC, Kennedy JG, Division AM (1989) Complementary mixed finite element formulations for elastoplasticity. Comput Methods Appl Mech Eng 74:177–206
Staron L (2008) Mobility of long-runout rock flows: a discrete numerical investigation. Geophys J Int 172:455–463
Tai Y-C, Noelle S, Gray JMNT, Hutter K (2002) Shock-capturing and front-tracking methods for granular avalanches. J Comput Phys 175:269–301
Tinti S, Bortolucci E, Vannini C (1997) A block-based theoretical model suited to gravitational sliding. Nat Hazards 16:1–28
Tits AL, Wachter A, Bakhtiari S, Urban TJ, Lawrence CT (2003) A primal-dual interior-point method for nonlinear programming with strong global and local convergence properties. SIAM J Optim 14:173–199
Varnes DJ (1978) Slope movement types and processes. In: Schuster RL, Krizek RJ (eds) Landslides analysis and control. Special Report, vol 176. Transportation Research Board¸National Academy of Sciences, New York, pp 11–33
Wang L, Zaniboni F, Tinti S, Zhang X (2019) Reconstruction of the 1783 Scilla landslide, Italy: numerical investigations on the flow-like behaviour of landslides. Landslides 16:1065–1076
Xia X, Liang Q (2018) A new depth-averaged model for flow-like landslides over complex terrains with curvatures and steep slopes. Eng Geol 234:174–191
Xu Q, Fan XM, Huang RQ, Westen C Van (2009) Landslide dams triggered by the Wenchuan Earthquake, Sichuan Province, south west China. Bull Eng Geol Environ 68:373–386
Zhang X, Krabbenhoft K, Pedroso DM, Lyamin AV, Sheng D, da Silva MV, Wang D (2013) Particle finite element analysis of large deformation and granular flow problems. Comput Geotech 54:133–142
Zhang X, Krabbenhoft K, Sheng D, Li W (2015) Numerical simulation of a flow-like landslide using the particle finite element method. Comput Mech 55:167–177
Zhang X, Sheng D, Sloan SW, Bleyer J (2017) Lagrangian modelling of large deformation induced by progressive failure of sensitive clays with elastoviscoplasticity. Int J Numer Methods Eng 112:963–989
Zhang X, Oñate E, Torres SAG, Bleyer J, Krabbenhoft K (2019) A unified Lagrangian formulation for solid and fluid dynamics and its possibility for modelling submarine landslides and their consequences. Comput Methods Appl Mech Eng 343:314–338
Acknowledgements
The author Liang Wang greatly appreciates financial support from the cooperation agreement between the University of Bologna and the China Scholarship Council (Grant No. 201606060161). The authors thank Dr. Gang Luo of Southwest Jiaotong University, Chengdu, Sichuan, China, for providing the engineering geological map of the Tangjiashan landslide.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, L., Zhang, X., Zaniboni, F. et al. Mathematical Optimization Problems for Particle Finite Element Analysis Applied to 2D Landslide Modeling. Math Geosci 53, 81–103 (2021). https://doi.org/10.1007/s11004-019-09837-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11004-019-09837-1