Geostatistics for Compositional Data: An Overview

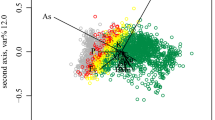
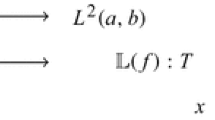Abstract

This paper presents an overview of results for the geostatistical analysis of collocated multivariate data sets, whose variables form a composition, where the components represent the relative importance of the parts forming a whole. Such data sets occur most often in mining, hydrogeochemistry and soil science, but the results gathered here are relevant for any regionalised compositional data set. The paper covers the basic definitions, the analysis of the spatial codependence between components, mapping methods of cokriging and cosimulation honoring compositional constraints, the role of pre- and post-transformations such as log-ratios or multivariate normal score transforms, and block-support upscaling. The main result is that multivariate geostatistical techniques can and should be performed on log-ratio scores, in which case the system data-variograms-cokriging/cosimulation is intrinsically consistent, delivering the same results regardless of which log-ratio transformation was used to represent them. Proofs of all statements are included in an appendix.

Appendices

Appendix A: Formal Statements and Proofs

In this appendix, proofs for the results in the main text are provided. They are organised into a “non-spatial” part and a spatial part. A few of these results have been published before, albeit mostly for ${\text {alr}}$, ${\text {clr}}$ or ${\text {ilr}}$ transformations. They are included for reasons of self-containedness and generality, as the expressions in this contribution are valid for any full rank log-ratio transformation. These pre-existing results are cited as appropriate. In what follows the variables ${\mathbf {z}}$ or ${\mathbf {Z}}$ will denote a composition in the original scale and $\varvec{\zeta }$ or $\varvec{Z}$ will be used for the log-ratio scores.

1.1 A.1 Non-spatial Results

Definition 1

(composition as a closed vector) A vector ${\mathbf {z}} \in \mathbb {R}^D$ is called a composition if its $k^{th}$ component $z_{k}$ represents the relative importance of part k with respect to the remaining components.

Typically, $z_{k}\ge 0$ and $z_{1}+z_{i}+\cdots +z_{D}=\kappa$, with $\kappa =1$ (for proportions), $\kappa =100$ (for percentages) and $\kappa =10^6$ (for ppm). However, the variables under consideration might only represent a subset of all possible variables in which case the constant sum constraint is not necessarily satisfied. Subsequent treatment of the data then depends on whether or not the resulting non-constant sum is meaningful and less than $\kappa$. In this case a fill-up variable (Eq. 2) can be added to retain that information and fulfill the constraint. On the other hand, if the non-constant sum is meaningless, the data can be reclosed (Eq. 3) without losing any information. Mathematically, this last case gives rise to the definition of compositions as equivalence classes (Barceló-Vidal 2003), the modern, more general definition of composition.

Definition 2

(log-ratio representation) A function $\psi (\cdot )$ is a full-rank log-ratio representation of the composition ${\mathbf {z}}$ if its image $\varvec{\zeta }$ satisfies

$$\begin{aligned} \varvec{\zeta }=\psi ({\mathbf {z}}) = \varvec{\varPsi }\cdot \ln {\mathbf {z}}, \end{aligned}$$

where $\varvec{\varPsi }$ is a $(D-1) \times D$ matrix of rank $(D-1)$ with $\varvec{\varPsi } \cdot {\mathbf {1}}_{D}={\mathbf {0}}_{D-1}$ (Barceló-Vidal and Martín-Fernández 2016).

Lemma 1

(inversion) If $\psi (\cdot )$ is a full-rank log-ratio transformation, then the corresponding matrix $\varvec{\varPsi }$ satisfies $\varvec{\varPsi }^{-}\cdot \varvec{\varPsi }={\mathbf {H}}$, where ${\mathbf {H}}$ is the projection matrix on the orthogonal complement of the vector ${\mathbf {1}}_{D}$ in $\mathbb {R}^D$ and $\varvec{\varPsi }^{-}$ is its generalized inverse.

Proof

The singular value decomposition of $\varvec{\varPsi }$ is given by $\varvec{\varPsi } = {\mathbf {U}}\cdot {\mathbf {S}} \cdot {\mathbf {V}}^t$, where ${\mathbf {U}}$ is an orthogonal $(D-1) \times (D-1)$ matrix, ${\mathbf {V}}$ is an orthogonal $D \times D$ matrix with ${\mathbf {V}}^t{\mathbf {V}}={\mathbf {I}}_{D}$ and ${\mathbf {S}}=\left[ \begin{matrix} {\mathbf {D}}_{(D-1)}&{\mathbf {0}}_{(D-1)} \end{matrix}\right]$ is a $(D-1) \times D$ matrix with ${\mathbf {D}}$ an invertible real diagonal matrix and ${\mathbf {0}}_{(D-1)}$ a column vector of zeros. The Moore-Penrose inverse is, therefore, $\varvec{\varPsi }^{-}={\mathbf {V}}\cdot {\mathbf {S}}^{+}\cdot {\mathbf {U}}^t$ where ${\mathbf {S}}^{+}=[{\mathbf {D}}^{-1} \ {\mathbf {0}}_{(D-1)}]^t$. Then

$$\begin{aligned} \varvec{\varPsi }^{-} \cdot \varvec{\varPsi }= & {} ({\mathbf {V}}\cdot {\mathbf {S}}^{+}\cdot {\mathbf {U}}^t) \cdot ({\mathbf {U}}\cdot {\mathbf {S}}\cdot {\mathbf {V}}^t) \\= & {} {\mathbf {V}}\cdot \left[ \begin{matrix} {\mathbf {I}}_{(D-1)} &{} {\mathbf {0}}_{(D-1)} \\ {\mathbf {0}}_{(D-1)}^t &{}0 \end{matrix}\right] \cdot {\mathbf {V}}^t. \end{aligned}$$

Since ${\mathbf {S}}^{+}\cdot {\mathbf {S}}$ has rank $D-1$ and ${\mathbf {V}}$ has full rank, $\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }$ has rank $D-1$ and its eigenvalues are 1 and 0. Since $(\varvec{\varPsi }^{-} \cdot \varvec{\varPsi })^2=\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }$, and $(\varvec{\varPsi }^{-} \cdot \varvec{\varPsi })^t=\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }$, the matrix $\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }$ is an orthogonal projection. Moreover from the definition of $\varvec{\varPsi }$ it follows that $\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }\cdot {\mathbf {1}}=\varvec{\varPsi }^{-} \cdot {\mathbf {0}}={\mathbf {0}}$. Therefore, if the columns of ${\mathbf {V}}$ are denoted by ${\mathbf {v}}_{i}, i=1, \dots ,D$, the eigenvector for 0 is given by ${\mathbf {v}}_{D} = \frac{1}{\sqrt{D}}{\mathbf {1}}$, so that $(\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }) = {\mathbf {I}}_{D}-{\mathbf {v}}_{D}{\mathbf {v}}_{D}^t = {\mathbf {I}}_D-\frac{1}{D}{\mathbf {1}}_{D\times D}={\mathbf {H}}$. $\square$

Proposition 1

(inverse log-ratio representation) A full-rank log-ratio representation $\psi (\cdot )$ is one-to-one, and its inverse is

$$\begin{aligned} {\mathbf {z}} = {\mathcal {C}}[\exp ( \varvec{\varPsi }^{-} \cdot \varvec{\zeta })]. \end{aligned}$$

Proof

From the previous lemma if follows that

$$\begin{aligned} {\mathcal {C}}[\exp ( \varvec{\varPsi }^{-} \cdot \varvec{\zeta })]= & {} {\mathcal {C}}[\exp ( \varvec{\varPsi }^{-} \cdot \varvec{\varPsi } \cdot \ln {\mathbf {z}})]\\= & {} {\mathcal {C}}[\exp ( ({\mathbf {H}} \cdot \ln {\mathbf {z}} )]\\= & {} {\mathcal {C}}[\exp ({\text {clr}}({\mathbf {z}})) ] \equiv {\mathbf {z}}. \end{aligned}$$

It remains to be shown that $\psi (\cdot )$ is one-to-one when restricted to the orthogonal complement of ${\mathbf {1}}_{D}$, but this is a direct consequence of the definition of $\psi (\cdot )$. $\square$

Proposition 2

(change of log-ratio representation) Let ${\mathbf {z}}$ be a composition, and $\psi _1(\cdot )$ and $\psi _2(\cdot )$ be two full-rank log-ratio transformations characterized by the matrices $\varvec{\varPsi }_1$ and $\varvec{\varPsi }_2$ respectively. Then, its two log-ratio representations $\varvec{\zeta }_1=\psi _1({\mathbf {z}})$ and $\varvec{\zeta }_2=\psi _2({\mathbf {z}})$ are related through the linear relationship

$$\begin{aligned} \varvec{\zeta }_2 = {\mathbf {A}}_{12}\cdot \varvec{\zeta }_1, \end{aligned}$$

(32)

where the matrix ${\mathbf {A}}_{12}=\varvec{\varPsi }_2\cdot \varvec{\varPsi }_1^-$ is square and invertible.

Proof

From the preceding two propositions it follows that $\varvec{\zeta }_2 = \psi _2({\mathbf {z}}) = \varvec{\varPsi }_2 \cdot \ln {\mathbf {z}}$ and ${\mathbf {z}} = {\mathcal {C}}[\exp ( \varvec{\varPsi }_1^{-} \cdot \varvec{\zeta }_1 )]$. Substituting the second expression into the first, one has

$$\begin{aligned} \varvec{\zeta }_2 = \varvec{\varPsi }_2 \cdot \ln \left( {\mathcal {C}}[\exp ( \varvec{\varPsi }_1^{-} \cdot \varvec{\zeta }_1 )] \right) = \varvec{\varPsi }_2 \cdot \left[ \varvec{\varPsi }_1^{-} \cdot \varvec{\zeta }_1 - \alpha {\mathbf {1}} \right] = \varvec{\varPsi }_2 \cdot \varvec{\varPsi }_1^{-} \cdot \varvec{\zeta }_1, \end{aligned}$$

where $\alpha =\ln ({\mathbf {1}}^t\cdot \exp (\varvec{\varPsi }_1^{-} \cdot \varvec{\zeta }_1))$. This last term satisfies $\kappa \varvec{\varPsi }_2\cdot {\mathbf {1}}={\mathbf {0}}$, which delivers the final expression as sought. $\square$

Proposition 3

(log-ratio representation of the mean) Let ${\mathbf {Z}}=[z_{kn}]$, $k=1,2,\ldots , D$, $n=1,2, \ldots , N$, be a compositional data set with N observations and of D parts, and $\psi (\cdot )$ be a full-rank log-ratio transformation. Then $\hat{\text {E}}\left[ \psi ({\mathbf {Z}})\right] =\psi (\hat{ {\varvec{\mu }^{g}}})$ the log-ratio representation of the closed geometric mean (Eq. 13).

Proof

The empirical closed geometric center is $\hat{{\mathbf {m}}} = {\mathcal {C}}[ \exp ( \ln ({\mathbf {Z}}) \cdot \varvec{1}_N/N ) ]$. The log-ratio mean is given by $\hat{\text {E}}\left[ \psi ({\mathbf {Z}})\right] =(\varvec{\varPsi } \cdot \ln {\mathbf {Z}})\cdot \varvec{1}_N/N$. Substituting this expression into the definition of the inverse log-ratio representation results in

$$\begin{aligned} \psi ^{-1}(\hat{\text {E}}\left[ \psi ({\mathbf {Z}})\right] )= & {} {\mathcal {C}}[\exp ( \varvec{\varPsi }^{-} \cdot \hat{\text {E}}\left[ \psi ({\mathbf {Z}})\right] )] = {\mathcal {C}}[\exp ( \varvec{\varPsi }^{-} \cdot \varvec{\varPsi } \cdot \ln ({\mathbf {Z}})\cdot \varvec{1}_N/N )] \\= & {} {\mathcal {C}}[\exp ( \ln ({\mathbf {Z}})\cdot \varvec{1}_N/N )] = \hat{ {\varvec{\mu }^{g}}}. \end{aligned}$$

$\square$

This proposition also proves Eq. (15): Because the calculation of $\hat{ {\varvec{\mu }^{g}}}$ does not involve any log-ratio representation, all log-ratio representations are equivalent. The idea of deriving statistics for compositional data from transformed scores is an application of the principle of working in coordinates (Mateu-Figueras et al. 2011).

Proposition 4

(log-ratio representations of the covariance) Let ${\mathbf {Z}}=[z_{kn}]$, $k=1,2,\ldots , D$, $n=1,2, \ldots ,N$, be a compositional data set with N observations and D parts, and $\psi (\cdot )$ be a full-rank log-ratio transformation. Then the covariance matrix of the log-ratio representation can be obtained from the empirical variation matrix $\hat{{\mathbf {T}}}$ as $\hat{\varvec{\varSigma }}^\psi = -\frac{1}{2} \varvec{\varPsi }\cdot \hat{{\mathbf {T}}}\cdot \varvec{\varPsi }^t$.

Proof

From (Aitchison 1986) it is known that the clr covariance $\hat{\varvec{\varSigma }}^c$ is related to the empirical variation matrix by $\hat{\varvec{\varSigma }}^c = -\frac{1}{2}{\mathbf {H}} \cdot \hat{{\mathbf {T}}}\cdot {\mathbf {H}}$ and $\varvec{\varPsi } \cdot {\mathbf {H}}=\varvec{\varPsi }$, which is a consequence the definition of the matrix ${\mathbf {H}}$ (Eq. 9), where

$$\begin{aligned} \varvec{\varPsi } \cdot {\mathbf {H}}= \varvec{\varPsi } \cdot \left( {\mathbf {I}}_{D\times D}-\frac{1}{D} {\mathbf {1}}_{D\times D} \right) = \varvec{\varPsi } \cdot {\mathbf {I}}_{D\times D}-\frac{1}{D} \varvec{\varPsi }{\mathbf {1}}_{D\times D} = \varvec{\varPsi } - \frac{1}{D}{\mathbf {0}}=\varvec{\varPsi }, \end{aligned}$$

because the rows of $\varvec{\varPsi }$ sum to zero. Therefore, it remains to be shown $\hat{\varvec{\varSigma }}^\psi = \varvec{\varPsi }\cdot \hat{\varvec{\varSigma }}^c\cdot \varvec{\varPsi }^t$. The (maximum likelihood) estimators of these two covariance matrices are

$$\begin{aligned} \hat{\varvec{\varSigma }}^\psi= & {} \frac{1}{N} \left( \varvec{\varPsi }\cdot (\ln ({\mathbf {Z}})-\ln ( \hat{{\varvec{\mu }^{g}}})\cdot \varvec{1} _N^t)\right) \cdot \left( (\ln ({\mathbf {Z}})-\ln (\hat{ {\varvec{\mu }^{g}}})\cdot \varvec{1}_N^t)^t \cdot \varvec{\varPsi }^t\right) , \\ \hat{\varvec{\varSigma }}^c= & {} \frac{1}{N} \left( {\mathbf {H}}\cdot (\ln ({\mathbf {Z}})-\ln (\hat{ {\varvec{\mu }^{g}}})\cdot \varvec{1}_N^t)\right) \cdot \left( (\ln ({\mathbf {Z}})-\ln (\hat{ {\varvec{\mu }^{g}}})\cdot \varvec{1}_N^t)^t \cdot {\mathbf {H}}\right) . \end{aligned}$$

Since ${\mathbf {H}}={\mathbf {H}}^t$, so that ${\mathbf {H}}\cdot \varvec{\varPsi }^t =\varvec{\varPsi }^t$, it follows that

$$\begin{aligned} \hat{\varvec{\varSigma }}^\psi= & {} \frac{1}{N} \left( \varvec{\varPsi } \cdot {\mathbf {H}}\cdot (\ln ({\mathbf {Z}})-\ln (\hat{ {\varvec{\mu }^{g}}})\cdot \varvec{1} _N^t)\right) \cdot \left( (\ln ({\mathbf {Z}})-\ln (\hat{ {\varvec{\mu }^{g}}})\cdot \varvec{1}_N^t)^t \cdot {\mathbf {H}}\cdot \varvec{\varPsi }^t\right) \\= & {} \varvec{\varPsi } \cdot \hat{\varvec{\varSigma }}^c \cdot \varvec{\varPsi }^t. \end{aligned}$$

Therefore $\hat{\varvec{\varSigma }}^\psi = \varvec{\varPsi } \cdot \hat{\varvec{\varSigma }}^c \cdot \varvec{\varPsi }^t= -\frac{1}{2} \varvec{\varPsi } \cdot {\mathbf {H}} \cdot \hat{{\mathbf {T}}}\cdot {\mathbf {H}}\cdot \varvec{\varPsi }^t= -\frac{1}{2} \varvec{\varPsi } \cdot \hat{{\mathbf {T}}}\cdot \varvec{\varPsi }^t$. $\square$

It is straightforward to show that the same properties hold for unbiased estimators (with denominator $N-1$).

The preceding two propositions show that the empirical log-ratio mean vector and covariance matrix can be obtained directly from the empirical closed geometric center and the variation matrix. Equivalent relationships exist also between the theoretical counterparts of these statistics.

Corollary 1

If $\psi (\cdot )$ is a full rank log-ratio transformation, then $\varvec{\varPsi }^{-} \cdot \hat{\varvec{\varSigma }}^\varPsi \cdot \varvec{\varPsi }^{-t} = \hat{\varvec{\varSigma }}^c$.

Proof

From Proposition 4 it follows that $\varvec{\varPsi }^{-} \cdot \hat{\varvec{\varSigma }}^\varPsi \cdot \varvec{\varPsi }^{-t}= \varvec{\varPsi }^{-} \cdot \varvec{\varPsi } \cdot \hat{\varvec{\varSigma }}^c \cdot \varvec{\varPsi }^t \cdot \varvec{\varPsi }^{-t}= {\mathbf {H}} \cdot \hat{\varvec{\varSigma }}^c\cdot {\mathbf {H}}^{t}=\hat{\varvec{\varSigma }}^c$. $\square$

Corollary 2

If $\psi _{1}(\cdot )$ and $\psi _{2}(\cdot )$ are full rank log-ratio transformations, then $\hat{\varvec{\varSigma }}^{\varPsi _2}={\mathbf {A}}_{12}\cdot \hat{\varvec{\varSigma }}^{\varPsi _1} \cdot {\mathbf {A}}_{12}^t$, where ${\mathbf {A}}_{12}=\varvec{\varPsi }_{2} \cdot \varvec{\varPsi }_{1}^{-}$.

Proof

From $\hat{\varvec{\varSigma }}^{\psi _2} = \varvec{\varPsi }_{2} \cdot \hat{\varvec{\varSigma }}^c \cdot \varvec{\varPsi }_{2}^t$ and Corollary 1 it follows that $\hat{\varvec{\varSigma }}^{\psi _2}=\varvec{\varPsi }_{2} \cdot \varvec{\varPsi }_{1}^{-} \cdot \hat{\varvec{\varSigma }}^{\psi _1} \cdot \varvec{\varPsi }_{1}^{-t}\cdot \varvec{\varPsi }_{2}^t={\mathbf {A}}_{12} \cdot \hat{\varvec{\varSigma }}^{\psi _1}\cdot {\mathbf {A}}_{12}^t$. $\square$

Corollary 3

If $\psi (\cdot )$ is a full rank log-ratio transformation, then $({\hat{\varvec{\varSigma }}^c})^{-}=\varvec{\varPsi }^{t} \cdot (\hat{{\varvec{\varSigma }}}^\psi )^{-1} \cdot \varvec{\varPsi }$ is a generalised inverse of $\hat{{\varvec{\varSigma }}}^c$.

Proof

Firstly, ${\hat{\varvec{\varSigma }}^\varPsi }$ has full rank and so is invertible, thus

$$\begin{aligned} {\hat{\varvec{\varSigma }}^c}\cdot (\hat{{\varvec{\varSigma }}^c})^{-}= & {} \varvec{\varPsi }^{-} \cdot {\hat{\varvec{\varSigma }}}^\psi \cdot \varvec{\varPsi }^{-t}\cdot \varvec{\varPsi }^{t} \cdot (\hat{{\varvec{\varSigma }}^\psi })^{-1} \cdot \varvec{\varPsi } \\= & {} \varvec{\varPsi }^{-} \cdot {\hat{\varvec{\varSigma }}^\psi } \cdot (\varvec{\varPsi } \cdot \varvec{\varPsi }^{-})^{t} \cdot (\hat{{\varvec{\varSigma }}}^\psi )^{-1}\cdot \varvec{\varPsi } \\= & {} \varvec{\varPsi }^{-} \cdot {\hat{\varvec{\varSigma }}}^\psi \cdot (\hat{\varvec{\varSigma }}^\psi )^{-1}\cdot \varvec{\varPsi } \\= & {} \varvec{\varPsi }^{-}\varvec{\varPsi }={\mathbf {H}}. \end{aligned}$$

since $(\varvec{\varPsi } \cdot \varvec{\varPsi }^{-})= {\mathbf {I}}_{(D-1)}$, so that $\hat{\varvec{\varSigma }}^c\cdot {(\hat{\varvec{\varSigma }}^c)}^{-}$ is symmetric. Secondly, ${\hat{\varvec{\varSigma }}^c}\cdot ({\hat{\varvec{\varSigma }}^c)}^{-} \cdot {\hat{\varvec{\varSigma }}^c}={\mathbf {H}} \cdot {\hat{\varvec{\varSigma }}}^c=\hat{\varvec{\varSigma }}^c$ and $({\hat{\varvec{\varSigma }}^c})^{-} \cdot \hat{\varvec{\varSigma }}^c \cdot ({\hat{\varvec{\varSigma }}^c})^{-} =({\hat{\varvec{\varSigma }}^c})^{-} \cdot {\mathbf {H}}=\varvec{\varPsi }^{t} \cdot ({\hat{\varvec{\varSigma }}^\psi })^{-1} \cdot \varvec{\varPsi }\cdot {\mathbf {H}} =({\hat{\varvec{\varSigma }}^c})^{-}$ Similarly, $({\hat{\varvec{\varSigma }}^c})^{-} \cdot \hat{\varvec{\varSigma }}^c={\mathbf {H}}$. Therefore, $\varvec{\varPsi }^{t} \cdot ({\hat{\varvec{\varSigma }}^\psi })^{-1} \cdot \varvec{\varPsi }$ satisfies all conditions of a generalised inverse. $\square$

Proposition 5

(invariance of the Mahalanobis distance) Let ${\mathbf {Z}}$ be a random composition, with variation matrix ${\mathbf {T}}$. The Aitchison–Mahalanobis distance between any two of its realisations ${\mathbf {z}}_1$ and ${\mathbf {z}}_2$

$$\begin{aligned} d_{M}^2({\mathbf {z}}_1,{\mathbf {z}}_2) = \psi ({\mathbf {z}}_1\ominus {\mathbf {z}}_2)^t \cdot [\varvec{\varSigma }^\psi ]^{-1} \cdot \psi ({\mathbf {z}}_1\ominus {\mathbf {z}}_2), \end{aligned}$$

is invariant under the choice of full-rank log-ratio representation $\psi (\cdot )$.

Proof

To show this proposition, it suffices to observe that from Corollary 3 and the proof of Proposition 4 one obtains ${\mathbf {H}}\cdot {(\varvec{\varSigma }^c)}^{-}\cdot {\mathbf {H}}={\mathbf {H}}\cdot \varvec{\varPsi }^{t} \cdot {({\varvec{\varSigma }}^\varPsi )}^{-1} \cdot \varvec{\varPsi }\cdot {\mathbf {H}}=\varvec{\varPsi }^{t} \cdot {(\varvec{\varSigma }^\varPsi )}^{-1} \cdot \varvec{\varPsi }$ so that

$$\begin{aligned} d_{M}^2({\mathbf {z}}_1,{\mathbf {z}}_2)= & {} \ln ({\mathbf {z}}_1 \ominus {\mathbf {z}}_2)^t \cdot \varvec{\varPsi }^{t} \cdot {(\varvec{\varSigma }^\varPsi )}^{-1} \cdot \varvec{\varPsi } \cdot \ln ( {\mathbf {z}}_1 \ominus {\mathbf {z}}_2 ) \\= & {} -2\ln ({\mathbf {z}}_1\ominus {\mathbf {z}}_2)^t\cdot \varvec{\varPsi }^t \cdot \varvec{\varPsi }^{-t} \cdot {\mathbf {T}}^{-}\cdot \varvec{\varPsi }^{-} \cdot \varvec{\varPsi }\cdot \ln ({\mathbf {z}}_1\ominus {\mathbf {z}}_2), \end{aligned}$$

an expression, which, given that $\varvec{\varPsi }^{-} \cdot \varvec{\varPsi }={\mathbf {H}}$, does not depend on the log-ratio representation at all.$\square$

Filzmoser and Hron (2008) proved a more restricted version of this proposition, valid for the set of ${\text {clr}}$, ${\text {alr}}$ and ${\text {ilr}}$ log-ratio transformations. Proposition 6 is a direct consequence of the invariance property of the Mahalanobis distance.

Proposition 6

(invariance of the normal distribution) The probability density function of the normal distribution on the simplex with center ${\mathbf {m}}$ and variation matrix ${\mathbf {T}}$,

$$\begin{aligned} f_{{\mathbf {Z}}}({\mathbf {z}}) = (2\pi )^{-(D-1)/2}|\varvec{\varSigma }^\psi |^{-1/2} \exp \left[ -\frac{1}{2} d_{M}^2({\mathbf {z}},{\mathbf {m}}) \right] , \end{aligned}$$

does not depend on the choice of full-rank log-ratio representation $\psi (\cdot )$.

Analogous results are available for the case when the log-ratio transformation is not full-rank. In that case the determinant $|\varvec{\varSigma }^\psi |$ needs to be generalised to the product of its non-zero eigenvalues. This invariance (Mateu-Figueras et al. 2013) is a direct consequence of the preceding Proposition 5 and the fact that the determinant of a matrix is one of its invariants.

1.2 A.2 Spatial Results

Definition 3

(compositional random function) A vector-valued random function ${\mathbf {Z}}=[Z_1,Z_2,\ldots , Z_D]$ on a spatial domain $\mathcal {D} \subset \mathbb {R}^p$, is called compositional if for each $x\in \mathcal {D}$ the vector of random variables ${\mathbf {Z}}(x)=[Z_1(x),Z_2(x),\ldots , Z_D(x)]$ shows the relative importance of a set of parts forming a total of interest.

Definition 4

(regionalized composition) Given a set of locations $\{x_1, x_2, \ldots , x_N\}$, a regionalized data set $\{ {\mathbf {z}}_1, {\mathbf {z}}_2, \ldots , {\mathbf {z}}_N \}$ with ${\mathbf {z}}_i={\mathbf {z}}(x_i)=[z_{1}(x_i), \ldots z_{D}(x_i)]=[z_{1i}, \dots , z_{Di}]$, $i=1,2, \ldots ,N$ is called a regionalized composition, if $z_{ki}$ represents the relative importance of part k with respect to the set of components considered at location $x_i$.

Proposition 7

(log-ratio representation of the spatial structure) Let ${\mathbf {Z}}=[z_{ki}]=[z_k(x_i)]$, $k=1,2,\ldots , D$, $i=1,2, \ldots ,N$, be a regionalized compositional data set with N locations $x_i$ and D parts, and $\psi (\cdot )$ be a full-rank log-ratio transformation. Then, for each lag h, the variogram of the log-ratio representation can be obtained from the empirical variation-variogram $\hat{{\mathbf {T}}}(h)$ as $\hat{\varvec{\varSigma }}^\psi (h) = -\frac{1}{2} \varvec{\varPsi }\cdot \hat{{\mathbf {T}}}(h)\cdot \varvec{\varPsi }^t$, or from the clr-variogram matrix as $\hat{\varvec{\varGamma }}^\psi (h) = \varvec{\varPsi }\cdot \hat{\varvec{\varGamma }}^c(h) \cdot \varvec{\varPsi }^t$.

This is a direct consequence of Propositions 3 and 4.

Proposition 8

(equivalence of the spatial structure) Let ${\mathbf {Z}}=[z_{kn}]=[z_k(x_n)]$, $k=1,2,\ldots , D$, $n=1,2, \ldots ,N$, be a regionalized compositional data set with N locations $x_n$ and D parts, and let $\psi _1(\cdot )$ and $\psi _2(\cdot )$ be two full-rank log-ratio transformations. Then, for each lag h, the empirical variograms $\hat{\varvec{\varGamma }}^{\psi _1}(h)$ and $\hat{\varvec{\varGamma }}^{\psi _2}(h)$ are related through the linear relationship

$$\begin{aligned} \hat{\varvec{\varGamma }}^{\psi _2}(h) = {\mathbf {A}}_{12}\cdot \hat{\varvec{\varGamma }}^{\psi _1}(h) \cdot {\mathbf {A}}_{12}^t, \end{aligned}$$

(33)

with matrix ${\mathbf {A}}_{12}=\varvec{\varPsi }_2\cdot \varvec{\varPsi }_1^-$ square and invertible.

Proof

From Proposition 7 it follows that $\hat{\varvec{\varGamma }}^{\psi _2}(h)= \varvec{\varPsi }_2 \cdot \hat{\varvec{\varGamma }}^c(h) \cdot \varvec{\varPsi }_2^t$; and because of Eq. (20), $\hat{\varvec{\varGamma }}^c(h)= \varvec{\varPsi }_1^{-} \cdot \hat{\varvec{\varGamma }}^{\psi _1}(h) \cdot \varvec{\varPsi }_1^{-t}$. Therefore

$$\begin{aligned} \hat{\varvec{\varGamma }}^{\psi _2}(h)= \varvec{\varPsi }_2 \cdot \varvec{\varPsi }_1^{-} \cdot \hat{\varvec{\varGamma }}^{\psi _1}(h) \cdot \varvec{\varPsi }_1^{-t} \cdot \varvec{\varPsi }_2^t, \end{aligned}$$

which proves the desired equality because ${\mathbf {A}}_{12}^t=\varvec{\varPsi }_1^{-t}\cdot \varvec{\varPsi }_2^t$. $\square$

Since Proposition 8 holds for all lags, it is normal to require that any fitted model satisfies the same relation. This is automatically satisfied if a linear model of coregionalization ${\mathbf {T}}(h|\varvec{\theta })$ is fitted to the variation-variograms and then recast to each of the two log-ratio representations via Proposition 7.

Proposition 9

(invariance of the cokriging predictor and errors) Let ${\mathbf {Z}}=[z_{kn}]=[z_k(x_n)]$, $k=1,2,\ldots , D$, $n=1,2, \ldots ,N$, be a regionalized compositional data set with N locations $x_n$ and D parts, and $\psi _1(\cdot )$ and $\psi _2(\cdot )$ be two full-rank log-ratio transformations. Then, the corresponding cokriging predictors $\hat{\varvec{\zeta }}_{1}(x_0)$ and $\hat{\varvec{\zeta }}_{2}(x_0)$ of the log-ratio transformed composition $\varvec{\zeta }_i(x_0) = \psi _i({\mathbf {Z}}(x_0))$ satisfy

$$\begin{aligned} \hat{\varvec{\zeta }}_{2}(x_0) = {\mathbf {A}}_{12}\cdot \hat{\varvec{\zeta }}_{1}(x_0), \end{aligned}$$

so that

$$\begin{aligned} \psi _1^{-1}(\hat{\varvec{\zeta }}_{1}(x_0)) = \psi _2^{-1}(\hat{\varvec{\zeta }}_{2}(x_0)) =: \hat{{\mathbf {z}}}(x_0), \end{aligned}$$

gives a predicted composition independent of the log-ratio representation used in the computations. Moreover, the corresponding cokriging error covariance matrices ${\mathbf {S}}_1$ and ${\mathbf {S}}_2$ are related by

$$\begin{aligned} {\mathbf {S}}_2^K = {\mathbf {A}}_{12}\cdot {\mathbf {S}}_1^K \cdot {\mathbf {A}}_{12}^t, \end{aligned}$$

with ${\mathbf {A}}_{12}=\varvec{\varPsi }_2\cdot \varvec{\varPsi }_1^-$, for all forms of cokriging (simple, ordinary, universal and cokriging with a trend) at all locations $x_0$, if both are derived from the same linear model of coregionalization ${\mathbf {T}}(h|\varvec{\theta })$.

Proof

The case of simple cokriging (SK) under the assumption of second-order stationarity will be considered first. In both log-ratio representations, the SK predictor is of the form

$$\begin{aligned} \hat{\varvec{\zeta }}(x_0) = \sum _{n=1}^N \varvec{\lambda }^t_{n} \varvec{\zeta }(x_n) = \varvec{\varLambda }^t \varvec{Z}, \end{aligned}$$

(34)

where $\varvec{Z}=[\varvec{\zeta }(x_1); \varvec{\zeta }(x_2);\ldots ; \varvec{\zeta }(x_N)]$ is the concatenated vector of all log-ratio transformed observations $\varvec{\zeta }(x_n)=\varvec{\varPsi }\ln {\mathbf {z}}(x_n)$, and $\varvec{\varLambda }=[\varvec{\lambda }_{1};\varvec{\lambda }_{2};\ldots ;\varvec{\lambda }_{N} ]$ is the block matrix of all cokriging weight matrices, which are obtained as (Myers 1982)

$$\begin{aligned} \varvec{\varLambda }=\underbrace{\left[ \begin{array}{cccc} \varvec{\varGamma }_{11} &{}\quad \varvec{\varGamma }_{12} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{1N}\\ \varvec{\varGamma }_{21} &{}\quad \varvec{\varGamma }_{22} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{2N}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \varvec{\varGamma }_{N1} &{}\quad \varvec{\varGamma }_{N2} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{NN}\\ \end{array} \right] ^{-1}}_{{\mathbf {W}}^{-1}} \underbrace{\left[ \begin{array}{c} \varvec{\varGamma }_{10} \\ \varvec{\varGamma }_{20} \\ \vdots \\ \varvec{\varGamma }_{N0} \end{array} \right] }_{{\mathbf {W}}_0} = {\mathbf {W}}^{-1} {\mathbf {W}}_0, \end{aligned}$$

where each block $\varvec{\varGamma }_{nm}=\varvec{\varGamma }(h|\varvec{\theta })=-\frac{1}{2} \varvec{\varPsi }{\mathbf {T}}(h|\varvec{\theta }) \varvec{\varPsi }^t$ using the fitted model ${\mathbf {T}}(h|\varvec{\theta })$. With the same notation, the SK error covariance is given by

$$\begin{aligned} {\mathbf {S}}^K = \varvec{\varGamma }_{00} - \varvec{\varLambda }^t {\mathbf {W}}_0=\varvec{\varGamma }_{00} - {\mathbf {W}}_0^t {\mathbf {W}}^{-1} {\mathbf {W}}_0. \end{aligned}$$

Considering these matrices obtained with the two distinct log-ratio representations, and taking Eq. (33) into account, then

$$\begin{aligned} {\mathbf {W}}^{(2)}= & {} \left[ \begin{array}{cccc} \varvec{\varGamma }_{11}^{(2)} &{}\quad \varvec{\varGamma }_{12}^{(2)} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{1N}^{(2)}\\ \varvec{\varGamma }_{21}^{(2)} &{}\quad \varvec{\varGamma }_{22}^{(2)} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{2N}^{(2)}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \varvec{\varGamma }_{N1}^{(2)} &{}\quad \varvec{\varGamma }_{N2}^{(2)} &{}\quad \cdots &{}\quad \varvec{\varGamma }_{NN}^{(2)}\\ \end{array}\right] \nonumber \\= & {} \left[ \begin{array}{cccc} {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{11}{\mathbf {A}}_{12}^t &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{12}{\mathbf {A}}_{12}^t &{}\quad \cdots &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{1N}{\mathbf {A}}_{12}^t\\ {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{21}{\mathbf {A}}_{12}^t &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{22}{\mathbf {A}}_{12}^t &{}\quad \cdots &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{2N}{\mathbf {A}}_{12}^t\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{N1}{\mathbf {A}}_{12}^t &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{N2}{\mathbf {A}}_{12}^t &{}\quad \cdots &{}\quad {\mathbf {A}}_{12}\varvec{\varGamma }^{(1)}_{NN}{\mathbf {A}}_{12}^t\\ \end{array}\right] \nonumber \\= & {} {\mathbf {A}} {\mathbf {W}}^{(1)} {\mathbf {A}}^t, \end{aligned}$$

(35)

where ${\mathbf {A}}={\text {diag}}({\mathbf {A}}_{12}, {\mathbf {A}}_{12}, \ldots , {\mathbf {A}}_{12})$ and similarly

$$\begin{aligned} {\mathbf {W}}^{(2)}_0 = {\mathbf {A}} {\mathbf {W}}_0^{(1)} {\mathbf {A}}_{12}^t. \end{aligned}$$

(36)

Now substituting Eqs. (35) and (36) into the expression for the weights

$$\begin{aligned} \varvec{\varLambda }^{(2)}= & {} [{\mathbf {W}}^{(2)}]^{-1} {\mathbf {W}}^{(2)}_{0}=[{\mathbf {A}}{\mathbf {W}}^{(1)}{\mathbf {A}}^t]^{-1} {\mathbf {A}}{\mathbf {W}}_0^{(1)}{\mathbf {A}}_{12}^t \nonumber \\= & {} {\mathbf {A}}^{-t}[{\mathbf {W}}^{(1)}]^{-1} {\mathbf {A}}^{-1}{\mathbf {A}}{\mathbf {W}}_0^{(1)} {\mathbf {A}}_{12}^t ={\mathbf {A}}^{-t}[{\mathbf {W}}^{(1)}]^{-1}{\mathbf {W}}_0^{(1)}{\mathbf {A}}_{12}^t \nonumber \\= & {} {\mathbf {A}}^{-t}\varvec{\varLambda }^{(1)}{\mathbf {A}}_{12}^t, \end{aligned}$$

(37)

which implies that the cokriging weight matrices of each datum satisfy

$$\begin{aligned} \varvec{\lambda }_n^{(2)} = {\mathbf {A}}_{12}^{-t} \varvec{\lambda }_n^{(1)} {\mathbf {A}}_{12}^t \end{aligned}$$

due to the block-diagonal structure of ${\mathbf {A}}$. Finally, substituting these weights into the SK predictor of the second log-ratio representation, and taking into account Eq. (32) between the data, one obtains

$$\begin{aligned} \hat{\varvec{\zeta }}_{2}(x_0)= & {} \sum _{n=1}^N [\varvec{\lambda }_{n}^{(2)}]^t \varvec{\zeta }_{2}(x_n) = \sum _{n=1}^N ( {\mathbf {A}}_{12}^{-t} \varvec{\lambda }_n^{(1)} {\mathbf {A}}_{12}^t)^t{\mathbf {A}}_{12} \varvec{\zeta }_1 (x_n) \\= & {} \sum _{n=1}^N {\mathbf {A}}_{12} [\varvec{\lambda }_n^{(1)}]^t {\mathbf {A}}_{12}^{-1} {\mathbf {A}}_{12} \varvec{\zeta }_1 (x_n) = {\mathbf {A}}_{12} \sum _{n=1}^N [\varvec{\lambda }_n^{(1)}]^t \varvec{\zeta }_1 = {\mathbf {A}}_{12}\hat{\varvec{\zeta }}_{1}(x_0), \end{aligned}$$

thus establishing the identity between the cokriging predictors. To derive the relation for the cokriging error covariance, the same strategy can be used to express the error in terms of the second log-ratio representation as a function of that in terms of the first representation,

$$\begin{aligned} {\mathbf {S}}^K_{(2)}= & {} \varvec{\varGamma }_{00}^{(2)} - [\varvec{\varLambda }^{(2)}]^t {\mathbf {W}}_0^{(2)} = {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{00}{\mathbf {A}}_{12}^t - [{\mathbf {A}}^{-t}\varvec{\varLambda }^{(1)}{\mathbf {A}}_{12}^t]^t {\mathbf {A}}{\mathbf {W}}_0^{(1)}{\mathbf {A}}_{12}^t\\= & {} {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{00}{\mathbf {A}}_{12}^t -{\mathbf {A}}_{12}[\varvec{\varLambda }^{(1)}]^t{\mathbf {A}}^{-1} {\mathbf {A}}{\mathbf {W}}_0^{(1)}{\mathbf {A}}_{12}^t \\= & {} {\mathbf {A}}_{12} \varvec{\varGamma }^{(1)}_{00}{\mathbf {A}}_{12}^t -{\mathbf {A}}_{12}[\varvec{\varLambda }^{(1)}]^t{\mathbf {W}}_0^{(1)}{\mathbf {A}}_{12}^t = {\mathbf {A}}_{12} \left[ \varvec{\varGamma }^{(1)}_{00} - [\varvec{\varLambda }^{(1)}]^t{\mathbf {W}}_0^{(1)}\right] {\mathbf {A}}_{12}^t\\= & {} {\mathbf {A}}_{12} {\mathbf {S}}^K_{(1)} {\mathbf {A}}_{12}^t, \end{aligned}$$

which proves the desired equivalence.

For the remaining cases of cokriging (which will be grouped under the name of universal cokriging, UK), the log-ratio mean is assumed to have the form

$$\begin{aligned} \varvec{\mu }(x) = \sum _{l=1}^L g_l(x) {\mathbf {b}}_l, \end{aligned}$$

with the typical cases $L=1$ and $g_1(x)\equiv 1$ (for ordinary cokriging), $g_l(x)=x^{l-1}$ up to the desired order L (universal cokriging), or $L=1$ and $g_1(x)$ an arbitrary function available everywhere in the estimation domain (for cokriging with a trend). In any case, the UK predictor has the same form (Eq. 34), where the weights are obtained from the solution of the system

$$\begin{aligned} {\mathbf {W}}\varvec{\varLambda } = {\mathbf {W}}_0, \end{aligned}$$

subject to the L unbiasedness conditions

$$\begin{aligned} \sum _{n=1}^N g_l(x_n) \varvec{\lambda }_n^t = g_l(x_0) {\mathbf {I}}_{D-1}, \quad \quad l=1,2, \ldots , L. \end{aligned}$$

where ${\mathbf {I}}_{D-1}$ is the identity matrix of size $(D-1)$, the dimension of the composition. It is known (Myers 1982; Tolosana-Delgado 2006) that this is equivalent to solving an extended system of equations

$$\begin{aligned} {\mathbf {W}}_e\varvec{\varLambda }_e = {\mathbf {W}}_{e0}, \end{aligned}$$

(38)

where

$$\begin{aligned} {\mathbf {W}}_e =\left[ \begin{array}{cc} {\mathbf {W}} &{}\quad {\mathbf {G}} \\ {\mathbf {G}}^t &{}\quad 0 {\mathbf {I}}_{L(D-1)} \\ \end{array}\right] , \quad \quad {\mathbf {W}}_{e0} = \left[ \begin{array}{c} {\mathbf {W}}_0 \\ {\mathbf {G}}^t_0 \\ \end{array}\right] , \quad \quad \varvec{\varLambda }_e = \left[ \begin{array}{c} \varvec{\varLambda } \\ {\mathbf {N}} \\ \end{array}\right] , \end{aligned}$$

with ${\mathbf {N}}^t=[\varvec{\nu }_1;\varvec{\nu }_2; \ldots ; \varvec{\nu }_L]$ the Lagrange multipliers for each unbiasedness condition, and ${\mathbf {G}}^t=[{\mathbf {G}}^t_1;{\mathbf {G}}^t_2; \ldots ; {\mathbf {G}}^t_N]$ with

$$\begin{aligned} {\mathbf {G}}_i = [g_1(x_i){\mathbf {I}}_{D-1}; g_2(x_i){\mathbf {I}}_{D-1};\ldots ; g_L(x_i){\mathbf {I}}_{D-1}], \quad \quad i=0,1,\ldots , N. \end{aligned}$$

The UK error covariance matrix is then shown to be

$$\begin{aligned} {\mathbf {S}}^K = \varvec{\varGamma }_{00} - \varvec{\varLambda }_e^t {\mathbf {W}}_{e0}=\varvec{\varGamma }_{00} - {\mathbf {W}}_{e0}^t {\mathbf {W}}_{e}^{-1} {\mathbf {W}}_{e0}. \end{aligned}$$

Since the UK and SK system of equations, predictors and errors have analogous forms, the proposition for the case of UK can be proved by showing that, if the extended matrices satisfy Eqs. (35)–(37), then they satisfy the UK system of equations (Eq. 38) as well. That is, if ${\mathbf {W}}_e^{(2)}={\mathbf {A}} {\mathbf {W}}_e^{(1)} {\mathbf {A}}^t$ (Eq. 35) and $\varvec{\varLambda }_e^{(2)}={\mathbf {A}}^{-t}\varvec{\varLambda }_e^{(1)}{\mathbf {A}}_{12}^t$ (Eq. 37), then in Eq. (38), becomes

$$\begin{aligned} {\mathbf {W}}_e^{(2)}\varvec{\varLambda }_e^{(2)} = [{\mathbf {A}} {\mathbf {W}}_e^{(1)} {\mathbf {A}}^t][{\mathbf {A}}^{-t}\varvec{\varLambda }_e^{(1)}{\mathbf {A}}_{12}^t]={\mathbf {A}} {\mathbf {W}}_e^{(1)}\varvec{\varLambda }_e^{(1)}{\mathbf {A}}_{12}^t= {\mathbf {A}} {\mathbf {W}}_{e0}^{(1)}{\mathbf {A}}_{12}^t={\mathbf {W}}_{e0}^{(2)}, \end{aligned}$$

which holds given Eq. (36).$\square$

Lastly, the relationship is established between the quadratures for distinct log-ratio representations $\psi _1(\cdot )$ and $\psi _2(\cdot )$. The weights $w_1, w_2, \ldots , w_k$ and quadrature points $u_1, u_2, \ldots , u_k$ do not depend on the choice of log-ratio representation. If $\hat{\varvec{\zeta }}_{i}$ is the predictor using the i-th log-ratio representation, then by Proposition 9 the representations $\hat{\varvec{\zeta }}_{1}$ and $\hat{\varvec{\zeta }}_{2}$ are related by ${\mathbf {A}}_{12}\cdot \hat{\varvec{\zeta }}_{1}=\hat{\varvec{\zeta }}_{2}$.

The spectral decomposition of the cokriging error covariance matrix ${\mathbf {S}}_1^K$ is given by ${\mathbf {S}}_1^K = {\mathbf {V}}_1\cdot {\mathbf {D}}_1\cdot {\mathbf {V}}_1^t$, where ${\mathbf {D}}_1$ is a diagonal matrix and ${\mathbf {V}}_1$ is an orthogonal matrix of eigenvectors then ${\mathbf {R}}_1 = {\mathbf {V}}_1\cdot {\mathbf {D}}_1^{1/2} \cdot {\mathbf {V}}_1^t$ is a square root of ${\mathbf {S}}_1^K$ and so from the congruence one has

$$\begin{aligned} {\mathbf {S}}_2^K = {\mathbf {A}}_{12}\cdot {\mathbf {S}}_1^K\cdot {\mathbf {A}}_{12}^t = {\mathbf {A}}_{12}\cdot ({\mathbf {V}}_1\cdot {\mathbf {D}}_1\cdot {\mathbf {V}}_1^t)\cdot {\mathbf {A}}_{12}^t. \end{aligned}$$

This expression can be rewritten as

$$\begin{aligned} {\mathbf {S}}_2^K= & {} {\mathbf {A}}_{12}\cdot {\mathbf {V}}_1\cdot {\mathbf {D}}_1^{1/2} \cdot {\mathbf {V}}_1^t \cdot ({\mathbf {A}}_{12}^{-1} \cdot {\mathbf {A}}_{12} ) \cdot {\mathbf {V}}_1\cdot {\mathbf {D}}_1^{1/2} \cdot {\mathbf {V}}_1^t\cdot {\mathbf {A}}_{12}^t \\= & {} ({\mathbf {A}}_{12}\cdot {\mathbf {R}}_{1} \cdot {\mathbf {A}}_{12}^{-1}) \cdot {\mathbf {A}}_{12} \cdot {\mathbf {R}}_{1} \cdot \cdot {\mathbf {A}}_{12}^t, \end{aligned}$$

and so

$$\begin{aligned} {\mathbf {R}}_{2}={\mathbf {A}}_{12}\cdot {\mathbf {R}}_{1} \cdot {\mathbf {A}}_{12}^t, \end{aligned}$$

is a square root of ${\mathbf {S}}_2$ if and only if ${\mathbf {A}}_{12}^t = {\mathbf {A}}_{12}^{-1}$, that is, ${\mathbf {A}}_{12}$ is an orthogonal matrix. In that case the quadrature vectors $\varvec{\zeta }(i_1, i_2, \ldots , i_{D-1})$ are related by

$$\begin{aligned} \varvec{\zeta }_{(2)}(i_1, i_2, \ldots , i_{D-1})= & {} \varvec{\zeta }_{2}+{\mathbf {R}}_{2}\cdot {\mathbf {u}}_{[i_1, i_2, \ldots , i_{D-1}]} \end{aligned}$$

(39)

$$\begin{aligned}= & {} {\mathbf {A}}_{12}\cdot \varvec{\zeta }_1 + {\mathbf {A}}_{12}\cdot {\mathbf {R}}_{1} \cdot {\mathbf {A}}_{12}^t \cdot {\mathbf {u}}_{[i_1, i_2, \ldots , i_{D-1}]} \end{aligned}$$

(40)

$$\begin{aligned}= & {} {\mathbf {A}}_{12}\cdot (\varvec{\zeta }_1 + {\mathbf {R}}_{1} \cdot \cdot {\mathbf {v}}_{[i_1, i_2, \ldots , i_{D-1}]}). \end{aligned}$$

(41)

where ${\mathbf {v}}_{[i_1, i_2, \ldots , i_{D-1}]}={\mathbf {A}}_{12} \cdot {\mathbf {u}}_{[i_1, i_2, \ldots , i_{D-1}]}$. Thus Gauss–Hermite quadratures are invariant under the choice of ${\text {ilr}}$ transformation only, but they are not affine equivariant.

Appendix B: Compositional Geostatistics Workflow

1.1 B.1 Interpolation

• 1. Perform both classical and compositional exploratory analysis (Sect. 3.4)

• 2. Compute variation-variograms of the regionalized composition (Eq. 22)

• 3. Fit a valid model (Sect. 5.2); models such as the linear model of coregionalization or the minimum/maximum autocorrelation factors are useful

• 4. Recast both the experimental and the model variation-variograms via other log-ratio transformation with respectively Eqs. (23) and (25), in order to confirm that the model fits the data reasonably well in these other reference systems with respect to these other log-ration representations

• 5. Choose one of these alternative log-ratio transforms, and compute the scores of the data (Eq. 10)

• 6. Apply cokriging to the log-ratio scores with variogram model expressed in the same log-ratios on a suitably chosen grid; store cokriging covariance error matrices if cross-validation or Gauss–Hermite quadratures is desired

• 7. Backtransform the predicted values

• 8. If unbiased estimates of the mass of each component are required and an ilr is being used, estimate them through Gauss-Hermite quadratures (Eq. 28); otherwise, follow the procedure in the Sect. B.2

• 9. Further products (maps, cross-validation, block models, etc) can be derived from individual components of the composition or from relevant log-ratios; cross-validation studies should focus on multivariate quantities and pairwise log-ratio plots (Sect. 6.2).

Steps (2) and (3) can alternatively be applied to data transform via a particular log-ratio transformation. In this case, step (4) should also explore the fit of the model to the variation-variograms, and step (5) can be applied to the same log-ratio set as in step (2). This is the strategy followed in the paper, where all calculations were primarily done with the alr-transformed data.

1.2 B.2 Simulation

• 1. Apply a log-ratio transformation to the data, then transform the scores via multivariate Gaussian anamorphosis, such as the flow anamorphosis (Sect. 7.2)

• 2. Estimate direct and cross-variograms of the Gaussian scores

• 3. Fit a valid joint model to these variograms

• 4. Apply conditional simulation algorithms to produce simulations of the Gaussian scores

• 5. Transform the simulated Gaussian scores to log-ratio scores with the inverse Gaussian anamorphosis, then backtransform the log-ratio scores to compositions

• 6. Post-process simulations as desired, that is, produce point-wise estimates of non-linear quantities (Eq. 27), upscale them to block averages (Eqs. 29–31) or produce maps.