Abstract
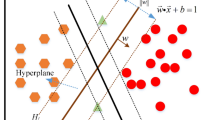
Two algorithms are outlined, each of which has interesting features for modeling of spatial variability of rock depth. In this paper, reduced level of rock at Bangalore, India, is arrived from the 652 boreholes data in the area covering 220 sq⋅km. Support vector machine (SVM) and relevance vector machine (RVM) have been utilized to predict the reduced level of rock in the subsurface of Bangalore and to study the spatial variability of the rock depth. The support vector machine (SVM) that is firmly based on the theory of statistical learning theory uses regression technique by introducing ε-insensitive loss function has been adopted. RVM is a probabilistic model similar to the widespread SVM, but where the training takes place in a Bayesian framework. Prediction results show the ability of learning machine to build accurate models for spatial variability of rock depth with strong predictive capabilities. The paper also highlights the capability of RVM over the SVM model.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Berger JO (1985) Statistical decision theory and Bayesian analysis. Springer, New York
Boser BE, Guyon IM, Vapnik VN (1992) A training algorithm for optimal margin classifiers. In: Haussler D (ed) 5th annual ACM workshop on COLT. ACM Press, Pittsburgh, pp 144–152
Cristianini N, Shawe-Taylor J (2000) An introduction to support vector machine. Cambridge University Press, Cambridge. www.support-vector.net
Kanevski, Maignan (2004) Analysis and modelling of spatial environmental data. PPUR
Kanevski M (ed) (2008) Advanced mapping of environmental data. Geostatistics, machine learning and Bayesian maximum entropy. iSTE and Wiley, New York
Li Y, Campbell C, Tipping M (2002) Bayesian automatic relevance determination algorithms for classifying gene expression data. Bioinformatics 18(10):1332–1339
MacKay DJ (1992) Bayesian methods for adaptive models. PhD thesis, Dep of Comput and Neural Syst. Calif Inst of Technol, Pasadena, CA
MathWork, Inc. (1999) Matlab user’s manual, Version 5.3. Natick, The MathWorks, Inc
Mukherjee S, Osuna E, Girosi F (1997) Nonlinear prediction of chaotic time series using support vector machine. In: Proc IEEE workshop on neural networks for signal processing, vol 7. Institute of Electrical and Electronics Engineers, New York, pp 511–519
Muller KR, Smola A, Ratsch G, Scholkopf B, Kohlmorgen J, Vapnik V (1997) Predicting time series with support vector machines. In: Proc int conf on artificial neural networks. Springer, Berlin, p 999
Radhakrishna BP, Vaidyanadhan R (1997) Geology of Karnataka. Geological Society of India, Bangalore
Scholkopf B (1997) Support vector learning. R. Oldenbourg, Munich
Sincero AP (2003) Predicting mixing power using artificial neural network. EWRI world water and environmental
Tipping M (2000) The relevance vector machine. Adv Neural Inf Process Syst 12:652–658
Tipping ME (2001) Sparse Bayesian learning and the relevance vector machine. J Mach Learn 1:211–244
Vapnik V (1995) The nature of statistical learning theory. Springer, New York
Vapnik V (1998) The nature of statistical learning theory. Wiley, New York
Vapnik V, Golowich S, Smola A (1997) Support method for function approximation regression estimation and signal processing. In: Mozer M, Petsch T (eds) Advance in neural information processing system, vol 9. MIT Press, Cambridge
Wahba G (1985) A comparison of GCV and GML for choosing the smoothing parameter in the generalized spline-smoothing problem. Ann Stat 4:1378–1402
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Samui, P., Sitharam, T.G. Applicability of Statistical Learning Algorithms for Spatial Variability of Rock Depth. Math Geosci 42, 433–446 (2010). https://doi.org/10.1007/s11004-010-9268-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11004-010-9268-7