Determination of the Period of Subcritical Growth of Internal Cracks in the Rail Head Under Operating Loads

We consider a computational model of loading of railroad rails in service under the operating conditions. We analyze main types of cracklike defects initiated in the railheads. On the basis of the energy approach of fracture mechanics, we construct a mathematical model for the evaluation of the period of subcritical growth of normal cracks in railheads. The obtained results of theoretical calculations are in good agreement with the averaged statistical data of scaled-down investigations.

The fatigue fracture of structural materials under the conditions of rolling contact is a quite frequent phenomenon in the engineering practice observed in the process of operation of wheel–rail technical couples and in the units of machines, such as the ball and roller bearings, rolls of rolling mills, gears, etc.

This is why the numerical evaluation of the durability of railroad rails with internal cracks is of high importance. The well-known approaches to the solution of this problem [1,2,3,4,5,6,7] do not take into account all operating factors of loading of the rails and do not give reliable results guaranteeing the possibility of prediction of their residual life.

Earlier, on the basis of the data of experimental investigations, the mechanisms of formation and propagation of cracks in operating rails and car wheels were analyzed and some conclusions were made in [1,2,3, 7]. In calculations [4,5,6], the authors used a two-dimensional model of fatigue fracture of rolling bodies and studied the development of edge fatigue macrocracks in the driven body of rolling couple under the conditions of dry friction and wetting, when the rolling load was modeled by the unidirectional cyclic motion of Hertzian contact forces. In these investigations, it was assumed that the cracks propagate according to the tensile mechanism.

In the present work, we try to adapt the well-known energy approach [8,9,10] to the determination of the period of subcritical crack growth in the heads of railroad rails with regard for the principal operating factors of their loading.

Computation Model of Loading of Railroad Rails

The stressed state in elements of railroad tracks can be found (with an accuracy sufficient for the practical purposes) by considering a rail as a beam of infinite length lying on the elastic base [1].

In this case, the distributions of the bending moment M and shear forces Q over the length of the rail under the action of a concentrated force P is described by the following dependences (the positive value of the moment corresponds to tensile stresses acting in the rail head):

$$ M=\frac{P}{4k}{e}^{- kx}\left(\sin kx-\cos kx\right),\kern0.5em Q=\frac{P}{2}{e}^{- kx}\cos kx, $$

(1)

where k is the coefficient of dynamic stiffness of the rail base, $k=\sqrt{U/4 EI}$, I is the moment of inertia of cross section relative to the horizontal axis, and x is the distance from the computed cross section to the point of application of the force.

The diagrams of shear forces and bending moment are alternating and, in the course of motion of the car wheels, their values undergo cyclic variations as functions of time. Thus, the rails fail under the conditions of complex stressed state caused by the normal and tangential stresses. However, in the cross sections where tensile stresses acting in the railhead attain their maximum values, the shear forces are equal to zero and the conditions of loading of the rail correspond to pure bending. On the other hand, a cyclic loading of this kind is also realized under the action of various quasistatic forces (temperature and residual stresses, longitudinal and lateral forces, etc.), which noticeably affect the total level of stresses (with a most pronounced increase of the total normal stresses). This enables us to assume that the normal stresses play the role of the main force factor specifying the durability of railroad rails under operating conditions and that the normal tension is the predominant mechanism of propagation of macrocracks.

The forces acting in the rail rapidly decrease as the distance from the point of application of the force increases and are close to zero for kx > π. Since the stiffness of the track is quite high (k ≈ 0.9–2 m^–1), we can neglect the mutual influence of the wheels located at distances greater than 4 m in practical calculations and restrict ourselves to the analysis of the wheeled carts of neighboring cars (Fig. 1). In that case, we obtain the following relation for the bending moment:

Fig. 1.

Distribution of the bending moment over the length of a rail: (І) car A; (II) car B.

$$ {\displaystyle \begin{array}{cc}M(x)=\sum \limits_i\frac{P_i}{4k}\upeta \left(k|x-{x}_i|\right),& \upeta \left(\upxi \right)={e}^{-\upxi}\left(\sin \upxi -\cos \upxi \right),\end{array}} $$

(2)

where P_i is a value of the force corresponding to the ith wheel and x_i is the coordinate of the point of its application.

The loads and specific features of the dynamics are different for each vehicle but, under high-cycle loads, in finding the durability of rails, we can assume that the load acting upon a wheel is constant (averaged under given operating conditions of the railroad):

$$ P-{k}_D\frac{P_0}{2}, $$

(3)

where P₀ is the mean axial load and k_D is the averaged value of the dynamic coefficient under given operating conditions of the railroad.

Formation of Cracks in the Rails

On the basis of the data of observations and conclusions made as a result of comprehensive investigations of the operation of railroad rails [7], we can specify three classes of cracks (according to the international nomenclature) formed on the surfaces of rail heads. These are

• cracks appearing under the surface at a distance of several millimeters from it and propagating parallel to the surface i.e., the so-called “schelling”-type cracks;

• small parallel scratches densely located on the upper and lateral surfaces of the heads, namely, the socalled “head-checking” cracks; they appear on arc tracks as a result of sliding and the action of strong contact forces leading to the formation of high plastic strains in the material;

• cracks initiated in a thin surface layer and propagating at a small angle to the surface, i.e., the socalled squat-type cracks.

The first and second classes of cracks are well studied, while the investigation of the third class of cracks has been originated only recently due to their frequent formation. They create serious problems in the lines with high-speed motion of passenger trains and are caused by the surface irregularities of the rail head appearing as a result of dynamic overloads in the case where the speed of motion of the trains increases.

Squat-type defects (Figs. 2a, b) form one of the most widespread classes of defects in railroad rails [4]. It was established that, on the surface of the driven element of the rolling couple, the macrocracks are formed and initially propagate by the mechanism of transverse shear at an acute angle to the rolling surface not only in the direction of motion of the load but also in the opposite direction (Fig. 2). The development of the left branch of the defect, i.e., in the direction of motion of the counterbody, unlike the development of the right branch, is accompanied by the branching both to the surface of the body and from the surface. After a certain time, the crack splits into two main cracks one of which propagates along the surface of the body and the other turns into the bulk of the rail. The mechanism of development of defects of this kind is not completely clear, especially in the case of branching into the depth of the material (see Fig. 2c).

Fig. 2.

Cracklike “squat”-type defect in the rail: (a) cross section; (b) outward appearance after the action of 1.5 ·10¹¹ kg of freight transportation; (c) possible mechanism of development; B is the direction of motion, C is the shear crack growth, D are possible causes of crack growth into the bulk of the rail (bending, friction, temperature stresses, residual stresses, and hydraulic effect).

Mathematical Model for the Evaluation of the Period of Subcritical Growth of a Normal Crack in the Rail Head

We now analyze the process of growth of a fatigue crack located in the cross section of the rail head (Fig. 3). In the experimental investigations, it was established [1] that, in the process of growth, these defects, as a rule, reproduce the shape of the head. This is why we assume that the contour of the crack is an oval of the fourth degree

Fig. 3.

Cross section of a rail containing a crack.

$$ {\left(\frac{x}{a}\right)}^4+{\left(\frac{y}{b}\right)}^4=1, $$

(4)

whose semiaxes satisfy the following relations:

$$ {\displaystyle \begin{array}{cc}b(N)={b}_0\upvarepsilon (N),& a(N)=b(N)\left(1+\left(\uplambda -1\right)\upvarepsilon (N)\right),\end{array}} $$

(5)

where λ = a₀ /b₀ and 2a₀ and 2b₀ are, respectively, the width and height of the rail head.

We now find the distribution of normal stresses in the rail head under given loading conditions:

$$ \upsigma ={\upsigma}_1+{\upsigma}_2+{\upsigma}_3, $$

(6)

where σ₁ and σ₂ are the normal stresses formed in the head under the action of the bending moment M(x) or in the case of contact interaction of a wheel with a rail (Hertz problem) and σ₃ are normal residual stresses appearing in the course of manufacturing of the rails.

The stresses σ₁ at the point A in the rail head are given by the formula [3]

$$ {\upsigma}_1=\frac{M}{I}H, $$

(7)

where I is the moment of inertia, H is the distance from the central axis to the center of the crack, and

$$ {\upsigma}_2(x)=\frac{G\sqrt{l^2-{x}^2}}{R\left(1-\upmu \right)}; $$

(8)

here,

$$ l=\sqrt{\frac{2 PR\left(1-\upmu \right)}{\uppi G}}, $$

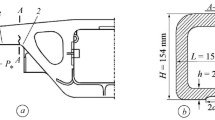
G is the shear modulus, μ is Poisson’s ratio, R is the radius of the wheel, and P is the load applied to the wheel and distributed over the thickness of the rail head (Fig. 4) [8].

Fig. 4.

Pressure of the wheel upon the rail.

In Fig. 5, we show the distributions of normal residual stresses plotted according to the results from [7] for different types of steels. For R65-type rails (GOST 8161-75, a₀ = 37 mm, b₀ = 21 mm, and H = 78.3 mm), by using relation (6) we get the distribution of normal stresses at the point A of the rail head (Fig. 3) for one loading block (Fig. 6).

Fig. 5.

Distributions of residual stresses for different types of steels [7]: (I) in the rail head; (II) in the rail web; (III) in the rail foot; (1) 90 steel; (2) 70 steel; (3) 110Cr steel; (4) 120 steel; (5) 110 steel.

Fig. 6.

Distributions of normal stresses: (І) car A; (ІІ) car B.

According to the assumptions made above, the sizes of the crack at any time are completely determined by the function ε(N). It is necessary to determine the number of loading cycles N^* for which the crack grows from an initial size (ε = ε₀) to the critical size (ε = ε_k). To solve this problem, we assume that the process of crack growth can be approximately regarded as continuous. We write the energy balance of crack growth for anytime t in the form [9]:

$$ A=W+\varGamma, $$

(9)

where A is the work of external forces, $W={W}_s+{W}_p^{(1)}(S)+{W}_p^{(2)}(t)-{W}_p^{(3)}(t)$ is the strain energy of the body, W_s is the elastic component of W, ${W}_p^{(1)}(S)$is the work of plastic strains depending only on the area of the crack S, ${W}_p^{(2)}(t)$ is the work of plastic strains done by external forces for a constant area of the crack in the course of tension of the process zone near the crack contour, which depends only on time t, ${W}_p^{(3)}(t)$ is the work of plastic strains spent for the unloading of the body and compression of the process zone, which is also performed for a constant area of the crack and depends only on time t, and Γ is the fracture energy of the body that depends solely on the crack area. Since the condition of energy balance is satisfied, the condition of balance of the rates of changes in these energies is also satisfied [10]:

$$ \frac{\partial \left[\varGamma -\left(A-{W}_s-{W}_p^{(1)}\right)\right]}{\partial S}\frac{dS}{dt}-\frac{\partial \left(A-{W}_s-{W}_p^{(2)}+{W}_p^{(3)}\right)}{\partial t}=0. $$

(10)

On the basis of the analysis of the components of Eq. (10), after their differentiation with regard for the dependences on the sizes S and t, by analogy with [10], for the evaluation of the crack growth rate V = dS/dt, we obtain

$$ \frac{dS}{dt}=\frac{W_C^{(0)}}{\upgamma -{\upgamma}_s}, $$

(11)

where γ is the density of the fracture energy of the material, γ_s is the density of the potential energy in the process zone at the maximum of stresses, and ${W}_C^{(0)}$ is the increment of energy ${W}_p^{(3)}$ per unit time.

Since in this case, the total loading is regarded as a block load with block period T (Fig. 6), we can multiply rate (11) by T to determine the crack growth rate under this load:

$$ \frac{dS}{dN}=\frac{W_C}{\upgamma -{\upgamma}_s}, $$

(12)

where N is the number of loading cycles, W_C is the increment of energy ${W}_p^{(3)}$ in a loading block. Equation (12), together with the initial conditions

$$ {\displaystyle \begin{array}{cc}\frac{t}{T}=N=0,& S(0)={S}_0,\end{array}} $$

(13)

and final conditions

$$ {\displaystyle \begin{array}{cc}\frac{t_{\ast }}{T}=N={N}_{\ast },& S\left({N}_{\ast}\right)={S}_{\ast },\end{array}} $$

(14)

forms a model for the determination of the residual life of a structural element (i.e., of the time t_* = N_*T) upon the attainment of which the crack area becomes equal to the critical size S_* and the body is destroyed.

We now write the equation for the strain energy of the body under block loading

$$ {W}_C={W}_{C^2}^{(1)}, $$

(15)

where ${W}_{C^2}^{(1)}$ is the dissipation of plastic strain energy in the process zone in a loading cycle.

By using the results of [10, 11], we obtain

$$ {\displaystyle \begin{array}{c}{\upgamma}_s=\frac{\upvarepsilon_{fC}}{\updelta_{fC}\varDelta S}\underset{L}{\int}\underset{0}{\overset{l_s}{\int }}{\upsigma}_t{\updelta}_{\mathrm{max}}\left(\upxi, x\right) dxd\upxi; \\ {}\begin{array}{cc}\upgamma =0.75{\upsigma}_t{\upvarepsilon}_{fC};& \varDelta S=\underset{L}{\int }{l}_s\left(\upxi \right)d\upxi; \end{array}\\ {}{W}_{C^2}^{(1)}=\frac{\upvarepsilon_{fC}}{\updelta_{fC}}\underset{0}{\overset{l_C}{\int }}\underset{L}{\int }{\upsigma}_t\left[{\updelta}_{\mathrm{max}}\left(\upxi, x\right)-{\updelta}_{\mathrm{min}}\left(\upxi, x\right)\right] dxd\upxi, \end{array}} $$

(16)

where ΔS is the area of the process zone near the crack contour, δ_max and δ_min are, respectively, the maximum and minimum opening displacements of a model notch along the process zone, δ_fC is its critical value corresponding to the critical strain ε_fC under cyclic loading, dξ is an increment of arc length along the crack contour L, l_f and l_s are the widths of the cyclic and static process zones, respectively l_c is the critical value of l_s, and σ_t is the mean value of tensile stresses in the process zone near the crack contour:

$$ {\upsigma}_t={\upsigma}_{0.2}+{A}_0{\left(\frac{\upvarepsilon_1}{\upvarepsilon_c}\right)}^n. $$

Here, A₀ = σ_s − σ_0.2, σ_s and σ_0.2 are, respectively, the ultimate strength and yield strength of the material of the body, n is the strain hardening exponent (it is assumed that n ≈ 1), and ε_c is the limit level of the strains ε₁.

It is known [10, 11] that

$$ \frac{\upvarepsilon_1}{\upvarepsilon_{fC}}=\frac{\updelta}{\updelta_{fC}}=\frac{K_{{\mathrm{I}}_{\mathrm{max}}}^2}{K_{fC}^2}. $$

Thus,

$$ {\upsigma}_t={\upsigma}_{0.2}+\left({\upsigma}_s-{\upsigma}_{0.2}\right)\frac{K_{{\mathrm{I}}_{\mathrm{max}}}^2}{K_{fC}^2}. $$

By using the well-known results from [12] and representing δ_max(ξ, x) and δ_min(ξ, x) via the stress intensity factors (SIF) K_Imax(ξ, x) and K_Imin(ξ, x), we can rewrite relation (12) with regard for (16) and (5) in the form

$$ \frac{d\upvarepsilon}{dN}=\frac{\upalpha_0}{4E{b}_0{\upsigma}_t}\left(\frac{\sum_{i=1}^{m_1}\left[{\left({K}_{\mathrm{Imax}}^{(i)}-{K}_{\mathrm{Imin}}^{(1)}\right)}^4-{K}_{\mathrm{th}}^4\right]}{K_{fC}^2-{K}_{\mathrm{Imax}}^{(2)}}\right). $$

(17)

Here, K_Imax(ξ, 0) and K_Imix(ξ, 0) are, respectively, the minimum and maximum values of K_I, K_th is the lower threshold value of K_I, m₁ is the number of loading cycles in a block, E is Young’s modulus, and α₀ is the coefficient of conversion of the static values of dissipation of plastic strain energy in the process zone into its experimentally obtained cyclic values [10, 11].

Equation (17) with the initial conditions

$$ {\displaystyle \begin{array}{cc}N=0,& \upvarepsilon (0)=\end{array}}{\upvarepsilon}_0 $$

(18)

and final conditions

$$ {\displaystyle \begin{array}{cc}N={N}_{\ast },& \upvarepsilon \left({N}_{\ast}\right)=\end{array}}{\upvarepsilon}_k $$

(19)

completely describes the kinetics of growth of fatigue cracks under block loading. The maximum value of the SIF is, in this case, attained at the point A (x = 0, y = b) [12] and, moreover,

$$ {K}_{\mathrm{I}}=\upsigma \sqrt{b_0}f\left(\upvarepsilon \right), $$

(20)

where the normal stresses are given by formula (6) and

$$ f\left(\upvarepsilon \right)=1.18\sqrt{\upvarepsilon}{\left\{0.32+\frac{0.68}{\sqrt{1-\upvarepsilon}}\right\}}^2{\left\{1+0.66\left(\frac{\upvarepsilon}{1}-\upvarepsilon \right)\right\}}^{-1/2}. $$

The durability of railroad rails is most often represented in terms of the freight mass (tonnage) transported through the analyzed section of the railroad:

$$ {T}_{\ast }=\frac{P_0}{g}m{N}_{\ast }, $$

(21)

where g is the gravitational acceleration and m is the number of wheel axles in the car.

Comparison of the Numerical Data with the Results of Durability Tests

For R65-type rails, the constants in Eq. (17) are as follows:

$$ {\displaystyle \begin{array}{c}\begin{array}{cccc}{\upsigma}_s=1180\mathrm{MPa},& {\upsigma}_{0.2}=900\mathrm{MPa},& E=2.1\cdot {10}^5\mathrm{MPa},& {K}_{\mathrm{th}}=3\mathrm{MPa}\cdot {\mathrm{m}}^{1/2},\end{array}\\ {}\begin{array}{ccc}{K}_{fC}=35\mathrm{MPa}\cdot {\mathrm{m}}^{1/2},& \mathrm{and}& {\upalpha}_0\approx 3\cdot {10}^{-4}.\end{array}\end{array}} $$

The initial crack size is chosen to guarantee that the area of the defect constitutes 20% of the cross sectional area of the head (which corresponds to ε₀ = 0.56). On the other hand, the minimum crack size for which the fracture of the rail is possible should be regarded as critical. According to the available experimental data [13], this size is equal to 30% of the total area of the head.

It is easy to see (Fig. 7) that the results of theoretical calculations are in good agreement with the mean statistical data of the scaled-down investigations of the rails [14].

Fig. 7.

Theoretical (dotted lines) and experimental (dashed lines) dependences of the lifetime of rail on the axial load: (1) 40–50 km/h; (2) 70–80 km/h.