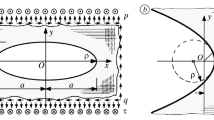
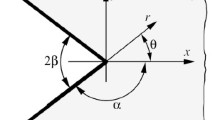
We consider the problem of stress distribution in an infinite quasiorthotropic plane containing an elliptic hole whose contour is free of external forces and a homogeneous stressed state is imposed at infinity. The solution of the problem is obtained with the help of the boundary transition from the known analytic solution for an elliptic hole in an orthotropic plane in the case where the roots of the characteristic equation approach each other. In the boundary case where the major semiaxis of the ellipse tends to infinity, these results yield the stress distribution in a plane weakened by a parabolic notch for two main types of deformation (symmetric tension and transverse shear).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
N. Hasebe and M. Sato, “Stress analysis of quasi-orthotropic elastic plane,” Int. J. Solids Struct., 50, 209–216 (2013).
N. Hasebe and M. Sato, “Mixed boundary-value problem for quasi-orthotropic elastic plane,” Acta Mech., 226, 527–545 (2015).
M. P. Savruk and A. B. Chornen’kyi, “Plane problem of the theory of elasticity for a quasiorthotropic body with cracks,” Fiz.-Khim. Mekh. Mater., 51, No. 3, 17–24 (2015); English translation: Mater. Sci., 51, No. 3, 311–321 (2015).
Z. Suo, G. Bao, B. Fan, and T. C. Wang, “Orthotropy rescaling and implications for fracture in composites,” Int. J. Solids Struct., 28, No. 2, 235–248 (1991).
F. E. Erdogan, M. Ratwani, and U. Yuceoglu, “On the effect of orthotropy in a cracked cylindrical shell,” Int. J. Fract., 10, No. 3, 369–374 (1974).
S. Krenk, “Influence of transverse shear on an axial crack in a cylindrical shell,” Int. J. Fract., 14, No. 2, 123–145 (1978).
I. S. Kostenko, “Elastic equilibrium of a closed orthotropic cylindrical shell with longitudinal notches,” Fiz.-Khim. Mekh. Mater., 16, No. 5, 67–70 (1980); English translation: Mater. Sci., 16, No. 5, 447–450 (1980).
V. P. Shevchenko, E. N. Dovbnya, and V. A. Tsvang, “Orthotropic shells with cracks (notches),” in: Stress Concentration (Mechanics of Composites) [in Russian], Vol. 7, A.S.K., Kiev (1998), pp. 212–249.
S. B. Cho, K. R. Lee, and Y. S. Choy, “A further study of two-dimensional boundary element crack analysis in anisotropic or orthotropic materials,” Eng. Fract. Mech., 43, No. 4, 589–601 (1992).
S. G. Lekhnitskii, Anisotropic Plates [in Russian], Gostekhizdat, Moscow (1957).
N. I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity [in Russian], Nauka, Moscow (1966).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 52, No. 3, pp. 7–14, May–June, 2016.
Rights and permissions
About this article
Cite this article
Kazberuk, A., Savruk, M.P. & Chornen’kyi, A.B. Stress Concentration Near an Elliptic Hole or a Parabolic Notch in a Quasiorthotropic Plane. Mater Sci 52, 295–304 (2016). https://doi.org/10.1007/s11003-016-9957-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-016-9957-6