Skip to main content
SpringerLink
Log in

Elastic Interaction of a Hole with Radial Surface Cracks of Different Length in the Isotropic Plate

  • Published:
Materials Science Aims and scope

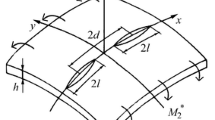
We consider the interaction of four surface cracks and a circular hole located in a thin isotropic plate. To solve this problem, we apply the method of boundary integral equations and the line-spring model. The system of boundary integral equations of this problem is solved numerically by the method of mechanical quadratures. The interaction of defects is revealed in the case of their location at small distances. We also compute the stress intensity factors at the crack tips and the stress concentration factors at the contour of the hole.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. P. F. Joseph and F. Erdogan, “Surface crack problems in plates,” Int. J. Fract. Mech., 41, 105–131 (1989).

    Article  Google Scholar 

  2. I. Rainah and M. P. Cartmell, “An analysis of the effects of the orientation angle of a surface crack on the vibration of an isotropic plate,” J. Phys., Conf. Ser., 382, No. 1, 012007 (2012).

    Google Scholar 

  3. J. R. Rice and N. Levy, “The part-through surface crack in an elastic plate,” Trans. ASME, Ser. J. Appl. Mech., 39, 185–194 (1972).

    Article  Google Scholar 

  4. V. P. Shevchenko, E. N. Dovbnya, and V. V Yartemik, “A shell of arbitrary curvature with a system of cracks of different types and geometries,” Prikl. Mekh., 47, No. 4, 89–98 (2011).

    Google Scholar 

  5. V. V. Bozhydarnik and O. V. Maksymovych, “Determination of the stressed state near edge cracks in a plate containing a hole of complex shape,” Fiz.-Khim. Mekh. Mater., 46, No. 1, 19–26 (2010); English translation: Mater. Sci., 46, No. 1, 16–26 (2010).

    Article  Google Scholar 

  6. E. N. Dovbnya, “A system of boundary integral equations for orthotropic shells of zero and negative curvatures weakened by cuts and holes,” in: Visn. Donetsk Univ., Ser. A: Natural Sciences, Issue 2 (1998), pp. 45–52.

  7. E. N. Dovbnya and N. A. Krupko, “Mathematical model of an isotropic plate with circular hole and nonthrough cracks,” Vestn. Khark. Nat. Tekh. Univ., No. 2 (45) (2012), pp. 130–134.

  8. G. N. Savin, Distribution of Stresses Near Holes [in Russian], Naukova Dumka, Kiev (1968).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Donetsk National University, Donetsk, Ukraine

    K. M. Dovbnya & N. A. Krupko

Authors
  1. K. M. Dovbnya
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. A. Krupko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. A. Krupko.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 50, No. 2, pp. 85–90, March–April, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dovbnya, K.M., Krupko, N.A. Elastic Interaction of a Hole with Radial Surface Cracks of Different Length in the Isotropic Plate. Mater Sci 50, 254–260 (2014). https://doi.org/10.1007/s11003-014-9715-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-014-9715-6

Keywords

Search

Navigation