Skip to main content
SpringerLink
Log in

Stressed State of a Hollow Conducting Sphere under the Electromagnetic Action in the Decaying Sinusoid Mode

  • Published:
Materials Science Aims and scope

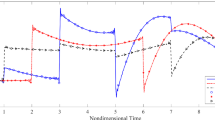
We formulate a dynamic centrally symmetric problem of thermomechanics for a hollow conducting sphere subjected to a homogeneous nonstationary electromagnetic action in the decaying sinusoid mode. We obtain the solution of this problem by using the cubic approximations of the azimuthal component of the vector of magnetic field and the radial component of the stress tensor in the radial coordinate. We also perform the numerical analysis of the thermal stressed state and the load-carrying capacity of nonferromagnetic spheres under the indicated conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. V. G. Bazhenov and M. V. Petrov, “On the application of the magnetic pulsed technique of deformation for the investigation of the viscoplastic characteristics of materials,” in: Applied Problems of Strength and Plasticity. Methods for the Solution of Problems of Elasticity and Plasticity [in Russian], Issue 37 (1980), pp. 18–25.

  2. Yu. V. Batygin, V. I. Lavinskii, and L. T. Khimenko, Pulsed Magnetic Fields for Advanced Technologies [in Russian], MOST-Tornado, Kharkov (2003).

    Google Scholar 

  3. Knoepfel, Pulsed High Magnetic Fields, North-Holland, Amsterdam (1970).

  4. G. S. Pisarenko and A A. Lebedev, Resistance of Materials to Deformation and Fracture in Complex Stressed State [in Russian], Naukova Dumka, Kiev (1969).

  5. F. Herlach (editor), Strong and Superstrong Magnetic Fields and Their Applications, Springer, Berlin (1985).

    Google Scholar 

  6. F. O. Moon, “Problem in magneto-solid mechanics,” Mechanics Today, 4, 307–309 (1978).

    Google Scholar 

  7. O. R. Hachkevych, R. S. Musii, and D. V. Tarlakovs’kyi, Thermomechanics of Nonferromagnetic Conducting Bodies under the Action of Pulsed Electromagnetic Fields with Amplitude Modulation [in Ukrainian], Spolom, Lviv (2011).

    Google Scholar 

  8. I. E. Tamm, Foundations of the Theory of Electricity [in Russian], Nauka, Moscow (1967).

    Google Scholar 

  9. V. F. Gribanov and N. G. Panichkin, Coupled and Dynamic Problems of Thermoelasticity [in Russian], Mashinostroenie, Moscow (1984).

    Google Scholar 

  10. A. D. Kovalenko, Foundations of Thermoelasticity [in Russian], Naukova Dumka, Kiev (1970).

    Google Scholar 

  11. W. Nowacki, Teoria Sprezystosci, PWN, Warszawa (1970).

    Google Scholar 

  12. Ya. S. Podstrigach and Yu. M. Kolyano, Generalized Thermomechanics [in Russian], Naukova Dumka, Kiev (1976).

  13. A. R. Gachkevich, R. S. Musii, and G. B. Stasyuk, “Thermomechanical state of a hollow conducting sphere under pulsed electromagnetic action,” Teor. Prikl. Mekh., Issue 40 (2005), pp. 9–17.

  14. R. S. Musii, Dynamic Problems of the Thermomechanics of Conducting Bodies of Canonical Shapes [in Ukrainian], Rastr-7, Lviv (2010).

  15. R. S. Musii, “Stressed state of a conducting sphere under the electromagnetic action with pulsed modulating signal,” Fiz.-Khim. Mekh. Mater., 46, No. 6, 76–81 (2010); English translation: Mater. Sci., 46, No. 6, 800–807 (2010).

  16. Ya. I. Burak, O. R. Hachkevych, and R. S. Musii, “Thermoelasticity of conducting bodies under the action of pulsed electromagnetic fields,” Mat. Metody Fiz.-Mekh. Polya, 49, No. 1, 75–84 (2006).

  17. R. S. Musii, “Formulation of boundary-value problems of the thermomechanics of conducting bodies of canonical shapes,” Fiz.-Khim. Mekh. Mater., 44, No. 5, 126–127 (2008); English translation: Mater. Sci., 44, No. 5, 735–737 (2008).

  18. O. R. Hachkevych and R. S. Musii, “Bearing ability of conducting elements of the canonical shape under the action of electromagnetic pulses,” Fiz.-Khim. Mekh. Mater., 46, No. 4, 92–97 (2010); English translation: Mater. Sci., 46, No. 4, 536–542 (2010).

  19. R. S. Musii, “Fundamental equation and solution of a centrally symmetric dynamic problem of thermoelasticity for a sphere in stresses,” Fiz.-Khim. Mekh. Mater., 38, No. 1, 117–118 (2002); English translation: Mater. Sci., 38, No. 1, 151–154 (2002).

  20. Ya. S. Podstrigach, Ya. I. Burak, A. R. Gachkevich, and L. V. Chernyavskaya, Thermoelasticity of Conducting Bodies [in Russian], Naukova Dumka, Kiev (1977).

Download references

Author information

Authors and Affiliations

  1. “L’vivs’ka Politekhnika” National University, Lviv, Ukraine

    R. S. Musii

Authors
  1. R. S. Musii
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. S. Musii.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 49, No. 2, pp. 97–104, March–April, 2013.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Musii, R.S. Stressed State of a Hollow Conducting Sphere under the Electromagnetic Action in the Decaying Sinusoid Mode. Mater Sci 49, 243–251 (2013). https://doi.org/10.1007/s11003-013-9606-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-013-9606-2

Keywords

Search

Navigation