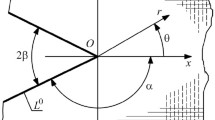
The method of singular integral equations was applied to determine the stress intensity factors for a system of cracks emanating from the vertex of an infinite rounded V-notch subjected to symmetric loading. The numerical values were obtained for two cases—the case of a single crack and the case of a system of two cracks of equal length. The influence of the rounding radius of the vertex of the notch and its opening angle on the stress intensity factors at the crack tips was analyzed. The solution obtained as a result has a general nature—the stress intensity factors at the crack tip are expressed as a function of the V-notch stress intensity factor and, hence, this solution could be treated as an asymptotic relation for finite bodies with deep V-notches subjected to symmetric loads.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. V. Panasyuk, P. M. Vitvitskii, and S. Ya. Yarema, “Plastic deformation around crack and fracture criteria,” Eng. Fract. Mech., 7, No. 2, 305–319 (1975).
V. V. Panasyuk and M. P. Savruk, “Plastic strips model in elastic-plastic problems of fracture mechanics,” Adv. Mech., 15. No. 3–4, 123–147 (1992).
D. Leguillon and Z. Yosibash, “Crack onset at a V-notch. Influence of the notch tip radius,” Int. J. Fract., 122, 1–21 (2003).
H. E. Doran, “The wedge with a symmetrical crack at the vertex in plane elastostatics,” J. Inst. Math. Appl.., 5, No. 4, 363–372 (1969).
F. Ouchterlony, “Symmetric cracking of wedge by concentrated loads,” Int. J. Eng. Sci., 15, No. 2, 109–116 (1977).
V. M. Aleksandrov, B. I. Smetanin, and B. V. Sobol’, Thin Stress Concentrators in Elastic Bodies [in Russian], Nauka, Moscow (1993).
M. P. Savruk and P. B. Rytsar, “A closed approximate solution of a plane problem of the theory of elasticity for a wedge with symmetric crack,” in: V. V. Panasyuk (editor), Fracture Mechanics of Materials and Strength of Structures [in Ukrainian], Vol. 2, Kamenyar, Lviv (1999), pp. 125–128.
M. P. Savruk and A. Kazberuk, “Relationship between the stress intensity and stress concentration factors for sharp and rounded notches,” Mater. Sci., 42, No. 6, 725–738 (2006).
M. P. Savruk, Two-Dimensional Problems of Elasticity for Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1981).
N. I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity [in Russian], Nauka, Moscow (1966).
J. P. Benthem, “Stresses in the region of rounded corners,” Int. J. Solids Struct., 23, No. 2, 239–252 (1987).
G. P. Cherepanov, Mechanics of Brittle Fracture [in Russian], Nauka, Moscow (1974).
M. L. Williams, “Stress singularities resulting from various boundary conditions in angular corners of plates in extension,” J. Appl. Mech., 19, No. 4, 526–530 (1952).
M. P. Savruk, P. N. Osiv, and I. V. Prokopchuk, Numerical Analysis in Plane Problems of the Theory of Cracks [in Russian], Naukova Dumka, Kiev (1989).
M. P. Savruk, Stress Intensity Factors in Bodies with Cracks [in Russian], in: V. V. Panasyuk (editor), Fracture Mechanics and Strength of Materials. A Handbook [in Ukrainian], Vol. 2, Naukova Dumka, Kiev (1988).
N. Hasebe and J. Iida, “A crack originating from triangular notch on a rim of semiinfinite plate,” Eng. Fract. Mech., 13, No. 7, 773–782 (1978).
M. P. Savruk and A. Kazberuk, “A unified approach to problems of stress concentration near V-shaped notches with sharp and rounded tip,” Int. Appl. Mech., 43. No. 2, 182–196 (2007).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Fizyko-Khimichna Mekhanika Materialiv, Vol. 45, No. 5, pp. 61–70, September–October, 2009.
Rights and permissions
About this article
Cite this article
Kazberuk, A. Stress intensity factors for cracks at the vertex of a rounded V-notch. Mater Sci 45, 676–687 (2009). https://doi.org/10.1007/s11003-010-9231-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-010-9231-2