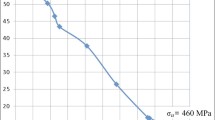
We have developed a mathematical model for determining residual stresses and stress concentration in the neighborhood of a plane joint of dissimilar materials and formulated variational statements of direct and inverse problems. The parameters of the stress–strain state of the object under study measured by nondestructive methods serve as input data for the inverse problem. We carry out a numerical analysis of solutions of the direct and inverse problems of determining stress concentration in the neighborhood of a joint of materials with different moduli. Finally, we discuss the applicability of the developed approach to the monitoring of the stress–strain state of joints in the course of their operation and to the evaluation of their residual life.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. V. Panasyuk, Mechanics of Quasibrittle Fracture of Materials [in Russian], Naukova Dumka, Kiev (1991).
S. P. Timoshenko, A Course in the Theory of Elasticity [in Russian], Naukova Dumka, Kiev (1972).
Ya. S. Podstrigach, V. A. Osadchuk, and A. M. Margolin, Residual Stresses, Long-Term Strength, and Reliability of Glass Structures [in Russian], Naukova Dumka, Kiev (1991).
A. Ya. Nedoseka, Foundations of Numerical Analysis and Diagnostics of Welded Structures [in Russian], Izd. “INDPROM,” Kiev (1998).
Ya. S. Pidstryhach, Selected Works [in Ukrainian], Naukova Dumka, Kyiv (1995).
V. F. Chekurin, “Mathematical problems of tomography of tensor fields in solids with residual stresses,” Mat. Metody Fiz.-Mekh. Polya, 46, No. 3, 133–148 (2003).
V. F. Chekurin and O. Z. Kravchyshyn, Elastic Disturbances in Nonuniformly Deformed Solids [in Ukrainian], Spolom, Lviv (2008).
V. F. Chekurin, “A variational method for the solution of direct and inverse problems of the theory of elasticity for a semiinfinite layer,” Izv. Ross. Akad. Nauk, Mekh. Tverd. Tela, No. 2, 58–70 (1999).
V. F. Chekurin and L. I. Postolaki, “A variational method for the solution of biharmonic problems for a rectangular domain,” Mat. Metody Fiz.-Mekh. Polya, 51, No. 1, 88–98 (2008).
L. V. Kantorovich and V. I. Krylov, Approximate Methods of Higher Analysis [in Russian], Fizmatlit, Moscow (1962).
L. M. Lobanov, V. A. Pivtorak, V. V. Savyts’kyi, and I. V. Kyyanets’, “Development of technology and apparatus for the diagnostics of structures made of metallic and composite materials based on the method of electronic shearography,” in: Problems of Service Life and Safety of Operation of Structures, Buildings, and Machines [in Ukrainian], Paton Institute of Electric Welding, Ukrainian National Academy of Sciences, Kyiv (2006), pp. 67–72.
V. F. Chekurin, “Inverse problem of nondestructive testing of the level of hardening of sheet glass,” Izv. Ross. Akad. Nauk, Mekh. Tverdogo Tela, No. 3, 86–97 (1998).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 45, No. 2, pp. 153–162, March–April, 2009.
Rights and permissions
About this article
Cite this article
Chekurin, V.F., Postolaki, L.I. Theoretical and experimental determination of residual stresses in plane joints. Mater Sci 45, 318–328 (2009). https://doi.org/10.1007/s11003-009-9181-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-009-9181-8