Seafloor multibeam backscatter calibration experiment: comparing 45°-tilted 38-kHz split-beam echosounder and 30-kHz multibeam data

Abstract

Obtaining absolute seafloor backscatter measurements from hydrographic multibeam echosounders is yet to be achieved. We propose a low-cost experiment to calibrate the various acquisition modes of a 30-kHz Kongsberg EM 302 multibeam echosounder in a range of water depths. We use a 38-kHz Simrad EK60 calibrated fisheries split-beam echosounder mounted at 45° angle on the vessel’s hull as a reference for the calibration. The processing to extract seafloor backscatter from the EK60 requires bottom detection, ray tracing and motion compensation to obtain acceptable geo-referenced backscatter measurements from this non-hydrographic system. Our experiment was run in Cook Strait, New Zealand, on well-known seafloor patches in shallow, mid, and deep-water depths. Despite acquisition issues due to weather, our results demonstrate the strong potential of such an approach to obtain system’s absolute calibration which is required for quantitative use of backscatter strength data.

Introduction

Seafloor acoustic backscatter data have received a high level of attention from the international scientific community over the last 10 years (e.g. Brown et al. 2011; Lurton and Lamarche 2015). It is now well accepted that such data provide qualitative information on substrate and benthic habitat (e.g. Brown and Blondel 2009; Lamarche et al. 2011; McGonigle and Collier 2014). Backscatter data are commonly acquired concomitantly with bathymetric data, at least with multibeam echosounders (MBES) which are presently the most widely used systems for acquisition of such data (Mayer 2006). Hydrographic data are widely used to inform sectors such as seabed infrastructure development, safety of navigation, environmental management or scientific research, to name a few. Consequently, the acquisition of bathymetric data, in particular using MBES, has been under scrutiny, similar to the use of satellite radar systems for Earth surface mapping. Hence, at present, strict and well-established standards and protocols are in place to ensure that bathymetric measurements are repetitive, systematic and comparable between systems.

Key to this is the requirement for absolute calibration of the acquisition systems. Such approaches have been well documented for bathymetric measurement using MBES echosounders and for fisheries echosounder (Foote et al. 1987; Demer et al. 2015; Guériot et al. 2000), as well as satellite radar systems (Elachi 1987; Luscombe and Thompson 2011). However, there is no clear procedure in place to calibrate the seafloor acoustic backscatter measurements from bathymetric MBES systems, and little literature is available on the subject. Such a procedure is, however, essential to provide quantitative information on the seafloor (Brown et al. 2015; Rice et al. 2015). The corollary is a lack of quantitative significance of backscatter data, with most data being only semi-quantitative, in that they are not comparable between systems. The lack of calibration was the prime issue identified by backscatter users in a recent survey (Lucieer et al. 2015). This problem of calibration hinders the uptake of backscatter capability by industry even though the technology and potential for applied science (hydrography, environmental monitoring, seafloor infrastructures, substrate mapping, etc.) are slowly being adopted by the private sector.

Three types of calibration for backscatter data or systems can be implemented (Lamarche and Lurton 2017): (1) in-factory (Brown et al. 2015); (2) absolute in-field, and (3) relative in-field (Rice et al. 2015) calibrations. Factory calibration, usually conducted in tanks, is undertaken at manufacturing time and is therefore the responsibility of the manufacturers. Relative calibration is commonly undertaken using patch-test areas prior to any given survey (Guériot et al. 2000). The absence of absolute calibration does not preclude undertaking a relative calibration, and likewise, a system calibrated at manufacturing time is most likely to require in-field relative or absolute calibration at some time. Absolute in-field calibration of MBES systems for backscatter intensity usually involves validation with a calibrated reference system, which adds logistical complexity and has rarely been implemented to date. The latter is the topic of this paper.

The aim here is to present a proof-of-concept approach of absolute in-field seafloor backscatter calibration of a Kongsberg EM 302 MBES using for reference a calibrated Simrad EK60 fisheries echosounder. We briefly present the operational procedures implemented on the field, which include mounting the fishery sounder at 45° angle on the vessel’s hull. The paper focuses on the data processing required to obtain a calibrated seafloor backscatter for the MBES system. For this project, we developed the entire processing sequence required to compare the backscatter datasets as there was none available. This functionality to produce seafloor backscatter measurements was added to NIWA’s open-source fisheries acoustics software ESP3 (Ladroit 2017). The EK60 system is not designed to produce geo-referenced soundings, and provides calibrated backscatter values for volumetric or single targets only. It does not account for sound velocity variability in the water column and does not compensate for vessel motion. The affordable approach described here is readily adaptable and could bring substantial benefits to seafloor backscatter research and applied initiatives by enabling a more generalized acquisition of calibrated seafloor backscatter.

Data acquisition

Acquisition systems

We used a Kongsberg EM 302 MBES system mounted on the National Institute of Water and Atmospheric Research’s (NIWA) vessel RV Tangaroa, a 70-m high-sea ship widely used for oceanic research in the Southwest Pacific Ocean. The frequency range of the EM 302 is 26.5–33.6 kHz, i.e. it is centered on 30 kHz (Kongsberg 2016). The system forms 288 beams and generates up to 864 soundings per ping in a 140° fan. The sounder antennas are hard-mounted in a pod underneath the vessel’s hull, and no hardware alterations were undertaken for this experiment. The RV Tangaora’s EM 302 provides 1° × 2° angular resolution. The EM 302 uses both Continuous Waves (CW) pulses and Frequency Modulation (FM) sweep pulses, with pulse compression on reception to increase the maximum useful swath width.

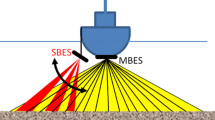
We used a Simrad EK60 split-beam echosounder, traditionally used for fishery surveys, to provide a backscatter reference level and enable us to calibrate the backscatter data acquired by the EM 302. The EK60 we used is a 38-kHz system coupled to an ES38-B transducer providing a 7° one-way beam aperture (Simrad 2012). For this experiment, the EK60 was mounted on the starboard side of the hull on a plate tilted at 45°, at the base of the moonpool which enabled easy deployment of the cabling (Fig. 1). The mounting plate was manufactured in NIWA’s workshop. The resulting angle between the face of the transducer and the back of the plate was measured and adjusted at 45° ± 1°. The plate was then mounted on the base (surveyed last in 2014) at the opening of the moonpool, giving good confidence that the resulting pointing angle of the transducer is within a 1° uncertainty.

This setting provides a means to compare measurements coming from the 45° angular sector. Although the frequencies of the EK60 and the EM 302 are not the same, we assumed that they are suitably close to enable a proper comparison and cross-calibration (see Discussion of this point in Sect. 4).

During acquisition, both systems were synchronized to ping alternately using a Kongsberg K-Sync unit (Kongsberg 2010), in order to avoid cross-talk.

Fig. 1

Setup of the Simrad EK60 and Kongsberg EM 302 sonars for the calibration experiment. Photo shows the EK60 array mounted on a 45° plate at the base of the moonpool (starboard side). Red horizontal line represents the EM 302 array, and the inclined blue line is that of the EK60. Sea surface and seafloor are represented by undulating lines. See text for explanation on the various parameters

Survey area

The experiment was undertaken in April 2015 in the eastern part of Cook Strait, New Zealand. We made use of the reference test-patch areas used by NIWA for in-field calibration of their MBES (Fig. 2). These sites are suitable for testing various ping modes available on the EM 302 (“Shallow”, “Medium”, “Deep”, “Very Deep”, and “Extra Deep”), and have been used for the past eight years to generate backscatter compensation curves and reference files for NIWA’s Kongsberg EM 300 and EM 302. The selected areas are flat, homogeneous in terms of sediment character and without significant seafloor backscatter features. The sediment homogeneity was confirmed by sample collection and corroborated by the homogeneous backscatter facies (Le Gonidec et al. 2003; Lamarche et al. 2011; Lucieer and Lamarche 2011). The sites are located close to the home port of RV Tangaroa, which optimizes and facilitates regular passages over the patch-test areas.

The backscatter lines were run on three depth ranges. The “Shallow” site at the southwestern boundary of Palliser Bay, lies in 115 m of water depth (Fig. 2). The “Medium” site is located on Palliser Bank, an isolated flat-floored area lying between 420 and 530 m of water, and delimited by the steep flanks of the Palliser and Opouawe Canyons (Mountjoy et al. 2009). The “Deep” site is located between 2220 and 2250 m of water depth in the approaches of the Hikurangi Trough, at the SE boundary of Cook Strait. These sites are suitable for the acquisition of backscatter data using the five ping modes of EM 302. Gain and frequency setups are specific to each mode and therefore the backscatter responses may differ from one mode to the other. All data were acquired in “Single” or “Dual Swath” mode (Table 1) using CW pulses only. However, this study is confined to data acquired in “Single Swath” mode, as this is considered to be the measurement configuration giving the most homogeneous backscatter response. This is in agreement with the recommendations of the international Backscatter Working Group (Lurton and Lamarche 2015). During the whole experiment, the EK60 was run with an identical pulse length of 1.024 ms and a transmitting power of 2 kW.

Fig. 2

Location of the survey lines in the NIWA shallow and medium depth patch test areas in Cook Strait, central New Zealand. Contours in metres are indicated. Note that only the “Shallow” and “Medium” sites are indicated as the “Deep” site was not used for this study (see text)

A significant low barometric pressure system sat over southeast New Zealand for part of the survey, with wind speeds ranging from 35 to 55 knots and peaking at 62 knots. The average wind speed over the entire voyage was 26 knots. Swell height peaked at 8–10 m and averaged 6–8 m. This resulted in the loss of 3.5 days of survey time.

Table 1 Summary of lines acquired

No EK60 data were acquired on the “Deep” site as the equipment did not perform to acceptable quality, and no extra-time could be allocated to the survey for later acquisition. Hence, no data from the “Deep” site were available for the calibration.

EK60 data processing methodology

The EK60 raw files generated by the General Purpose Transceiver contains datagrams for received power $P_{rx}s(t),$ as well as for along-ship and across-ship interferometric phase, as a function of time, for each ping. The EM 302 raw files include backscatter values for each sounding in separate datagrams. To enable comparison between the two systems, we extracted across-ship angle ($\theta$), along-ship angle ($\phi$), volumetric backscatter ($S_v$), and single target backscatter ($S_p$) values from $P_{rx}(t)$ using the system parameters provided by the manufacturer and the calibration values obtained during a tank calibration of the system. Key to this experiment was the need to geo-reference the EK60 soundings using bottom detection, ray tracing and motion compensation, then compute their backscatter values by applying the beam pattern and area compensation. No compensation was applied for the effect of incident angle, as the idea here is to compare the raw backscatter level from two instruments seeing the seafloor with a similar angle.

The entire EK60 processing sequence was coded in Matlab® and incorporated in NIWA’s custom-built fisheries acoustic data processing software ESP3®. It can be found in file bs_analysis.m on ESP3 repository (Ladroit 2017).

Bottom detection

In fisheries acoustics, the bottom is usually detected as the first strong return of the signal, and its contribution is removed from further analysis. Here, in contrast, recording and processing of the bottom echo are essential.

For the EK60 data, the bottom was detected separately on $S_v,$ $\theta$ and $\phi$ (Fig. 3). Detection was successful and reliable on both the across-ship angle and the volumetric backscatter for all lines, as the survey was run over a relatively flat seafloor. However this resulted in an along-ship angle close to null, giving no usable interferometric measurement. Hence, we assume that every EK60 sounding originated from the beam-centre in the along-ship plane. On the across-ship plane, we measured a long phase ramp (with a good signal-to-noise ratio) usable to generate multiple soundings per ping. Soundings originating from the interferometric phase were limited to angles inside the 3-dB two-way beam aperture (in this case ± 2.5°). These soundings were obtained using the same process as inside the beam of a MBES running in High-Density mode, but extending this method to all samples (Llort-Pujol et al. 2006).

Fig. 3

Bottom detection on EK60 data applied separately on $S_v$ (right), and both interferometric across-ship (left) and along-ship (centre) angles. Detection on along-ship angle fails to give good measurement as no ramp can be consistently found because of the close to nadir incidence on this plan. Detection on $S_v$ gives good results consistent with across-angle

This process generates time of arrival and angle position $(\theta ,\phi )$ referenced to the beam and signal power value $P_{rx}(t).$ Given the relatively flat seafloor chosen for this experiment, and for reasons stated above, we assume that $\phi =0.$

Ray tracing and motion compensation

Ray tracing and motion compensation are required here to calculate the accurate positioning of the soundings. Since most fisheries echosounders are mounted for vertical transmission, a constant average sound velocity profile (SVP) is assumed in the water column to calculate the range. Here, the EK60 was tilted at 45° beneath the vessel and this constant-velocity assumption is likely to be a significant source of error, especially in deeper sites. To account for possible variations in sound velocity in the water column, SVPs were collected every second line and included in the analysis to ensure proper and robust geo-referencing of the EK60 samples. We applied a simple ray-tracing method (Lurton 2010) by splitting SVPs into linear segments (Eq. 1).

The SVP inside layer n is defined as follows:

$$\begin{aligned} c(z)=c_n+g_n(z-z_n) \end{aligned}$$

(1)

where $c_n$ is the sound speed at depth $z_n,$ and $g_n$ is the sound speed gradient between the depth $z_n$ and $z_{n+1}.$

The Snell–Descartes law (Eq. 2) can be applied between those layers relating the incidence angle values $\theta _n$ to the local sound velocity $c_{n} {\text{:}}$

$$\begin{aligned} \xi =\frac{\sin \theta _n}{c_n}=\frac{\sin \theta _{n+1}}{c_{n+1}} \end{aligned}$$

(2)

Finally, the ray trajectory is described by:

$$\begin{aligned} \begin{aligned} r_{n+1}-r_n&=\frac{1}{\xi g_n}\left[ \sqrt{1-\xi ^2c^2(z_n)}-\sqrt{1-\xi ^2c^2(z_{n+1})}\right] \\ \tau _{n+1}-\tau _n&=\frac{1}{|g_n|}\ln \left( \frac{c(z_{n+1})}{c(z_n)}\frac{1+\sqrt{1-\xi ^2c^2(z_{n+1})}}{1+\sqrt{1-\xi ^2c^2(z_n)}}\right) \end{aligned} \end{aligned}$$

(3)

where $r_n$ is the lateral range to the transducer at time $\tau _n,$ provided that $\xi ^2c^2(z_{n+1})\ge 1.$

We use these equations to calculate the ray path (Fig. 4) based on the original transmitted angle, calculated from pitch ($\phi _p$), roll ($\theta _r$) and beam pointing angle values ($\theta _{EK60},\phi _{EK60}$).

Fig. 4

Sound velocity profile (SVP) (left) for the first lines on the “Medium” depth site (lines #008 and #009), and resulting ray tracing (right) for ping 1 of EK60 file D20150523-T113456. r(m) in Eq. (3) is the lateral distance to the ship in the plan defined by the ship’s vertical and the direction of transmission

We process the ray path for the beam centre of each ping based on the pitch and roll data ($\theta$ and $\phi$), and position the other soundings with the acrosship-angle value coming from the EK60. This provides a position for each sounding that is compensated for pitch and roll and referenced to the transducer centre T, of coordinates $(x_t,y_t,z_t)$ in the ship-relative coordinate system. Those soundings are subsequently translocated to EM 302 coordinates system compensating for the motion of the transducer face, adding $(x_{corr},y_{corr},z_{corr})$ to the previously computed position (Eq. 4).

$$\begin{aligned} \left( \begin{array}{c} x_{corr} \\ y_{corr} \\ z_{corr} \end{array} \right) = \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos \phi _p &{} \sin \phi _p \\ 0 &{} -\sin \phi _p &{} \cos \phi _p \end{array} \right) \left( \begin{array}{ccc} \cos \theta _r &{} 0 &{} \sin \theta _r \\ 0 &{} 1 &{} 0 \\ -\sin \theta _r &{} 0 &{} \cos \theta _r \end{array} \right) \left( \begin{array}{c} x_t \\ y_t \\ z_t \end{array} \right) -\left( \begin{array}{c} 0 \\ 0 \\ h \end{array} \right) \end{aligned}$$

(4)

where $(x_t,y_t,z_t)$ are the transducer coordinates as referenced to the ship, and h is the heave. Yaw cannot be included in the motion compensation as it is not logged in the EK60 “*.raw” files.

The soundings after ray-tracing/motion compensation show a significantly decreased depth variability dz compared to the uncompensated ones (Fig. 5 and 6). Considering the significant motion amplitude experienced during the survey, due essentially to the harsh sea state, we consider this result as demonstrating that the motion compensation was applied satisfactorily. Also, we compared the sounding positions computed with and without ray-tracing (assuming a constant sound velocity), and we observed a mean difference in position of 9 m on the “Shallow” site and 20 m on the “Medium” site, showing that in our case, the ray-tracing process was necessary. Differences in position are also illustrated by the resulting along and across distance positions of sounding after the ray-tracing/motion compensation process (lower two panels on Fig. 5).

Fig. 5

Beam-centre soundings obtained from the EK60 before (red) and after (blue) ray tracing and motion correction on file D20150523-T065817.raw (line #000 and #001, “Shallow” site)

Fig. 6

Soundings obtained from the EK60 beam before (bottom) and after (top) ray tracing and motion correction on file D20150523-T085128.raw (“Shallow” site)

This processing stage resulted in properly positioned soundings in latitude and longitude, making it possible to grid the resulting backscatter.

Beam pattern and insonified area compensation

Each bottom sample is associated with a received power $P_{rx}$ used to derive an uncompensated backscatter level $BS_{uncomp}$ thus:

$$\begin{aligned} BS_{uncomp}=10\log (P_{rx})+40\log (R)+2\alpha R-10\log \left( \frac{P_{tx}\lambda ^2}{16\pi ^2}\right) -2G \end{aligned}$$

(5)

where $R=c\tau /2$ is calculated using equations (3), $\lambda$ is the wavelength, $P_{tx}$ the transmitted power, $\alpha$ is the absorption coefficient, and G is the transducer one-way gain obtained during calibration.

The beam pattern of the EK60 transducer used here is well documented (Jech et al. 2005), and is regularly checked as part of the calibration process (e.g. before fisheries surveys). The two-way beam pattern of the transducer was measured prior to this experiment in a tank, and the results showed a root-mean square difference between the Simrad beam model (Jech et al. 2005) and the measurements of less than 0.2 dB out to 6°. The beam pattern model writes (in dB):

$$\begin{aligned} \begin{aligned} F_{comp}(\theta ,\phi )&=6.0206(u_{al}^2(\theta )+u_{ac}^2(\phi )-0.18 u_{al}^2(\theta ) u_{ac}^2(\phi ))\\ u_{al}(\theta )&=2\theta /BW_{al}\\ u_{ac}(\phi )&=2\phi /BW_{ac} \end{aligned} \end{aligned}$$

(6)

where $BW_{al}$ and $BW_{ac}$ are the along-ship and across-ship one-way beamwidths. Here $BW_{al}=BW_{ac}=\theta _{3dB}=7^\circ.$ The resulting two-way beam pattern for the transducer is, in natural units:

$$\begin{aligned} bp(\theta ,\phi )=10^{\frac{1}{10}(\max (F_{comp})-F_{comp}(\theta ,\phi ))} \end{aligned}$$

(7)

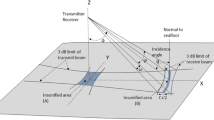
In a first-order approximation, we assume that the intersection of the one-way beam with the flat seafloor is an ellipse of major half-axis $a=R_{EK60}\sin ({\theta _{3dB}/2})/\cos {\theta _{EK60}}$ and minor half-axis $b=R_{EK60}\sin ({\theta _{3dB}/2})$ (Fig. 7), where $R_{EK60}$ and $\theta _{EK60}$ are respectively the slant range and the incident angle associated to the EK60 measurements (Fig. 1).

Fig. 7

Approximated insonified area for the tilted EK60 one-way beam (blue) and for the contribution to one sample (red stripped), where $dR=cT/2$ with T the pulse length

Therefore, each sample received at $t=2R/c$ originates from a contributing seafloor area A(R) (Eq. 8) used for signal compensation. Later in the process the analysis is restricted on the across-track dimension to half the one-way beamwidth, so that the outer part of the ellipse is not included in the calculation. Inside this angular sector, the approximation is justified by the fact that when pointing at 45°, the ratio between the approximated slice area and the actual area of the ellipse slice stays above 85%, which causes a bias smaller than 0.7 dB, staying within the expected accuracy of the resulting measurement.

$$\begin{aligned} A(R)\approx R\sin \frac{\theta _{3dB}}{2}\frac{c\tau }{\sin \theta _{EK60}} \end{aligned}$$

(8)

We add a corrective term $bp_{comp}$ (Eq. 9) based on the beam pattern to account for the fact that this area is not uniformly insonified by the beam on the along-ship direction (x in Fig. 7).

$$ bp_{{comp}} = \int\limits_{{ - \theta _{{3dB}} /2}}^{{\theta _{{3dB}} /2}} {bp(0,\phi )/\theta _{{3dB}} d\phi } $$

(9)

This corrective factor also accounts for the fact that we are considering an insonified area produced by a wider angle that the two-way beam angle aperture of the system in the along direction, and gives an equivalent result to the calculation of the two-way equivalent beam angle used in Weber and Ward (2015). We obtain $bp_{comp}=4.9^\circ /\theta _{3dB}\approx 0.68.$

Finally, we calculate the compensated backscatter strength value BS for each sample:

$$\begin{aligned} BS=BS_{uncomp}-10\log (bp_{comp}A(R)) \end{aligned}$$

(10)

Figure 8 shows the effect of the beam pattern compensation on line #000 and #001. The compensated result is homogeneous and no longer shows across-ship angular dependency.

Fig. 8

Seafloor backscatter from EK60 before and after beam pattern compensation on file D20150523-T065817.raw (“Shallow” site, lines #000 and #001)

It is now possible to use the resulting backscatter data computed in Sect. 2.2 to generate a geo-referenced backscatter grid (or mosaic) using the positions of each sounding. Those data were gridded using a 5-m step for the “Shallow” site, and 15-m step for the “Medium” site, using an unweighted mean direct gridding method.

EM 302 backscatter

The EM 302 backscatter was obtained from the “Seabed Image” datagram contained in the *.all files, using the SonarScope® software of Ifremer (Augustin 2017). The backscatter was subsequently gridded using the same grid size and gridding method as for the EK60 reflectivity.

Results

In Section 2, two comparable geo-localised backscatter grids have been produced for the EK60 and EM 302 data. We now compare the backscatter levels generated by the two systems from the lines run in “Single swaths”. These are lines#000, 001, 004, 005 for the “Shallow”site, and lines #008, 009, 012, 013 for the “Medium” site, so that for each site, four lines are run in two different EM 302 modes.

EK60 self-comparison

We compute the mean EK60 backscatter for each of the four lines on the two sites and compare them line by line (Table 2). For the “Shallow” site, the means range from − 20.9 to − 20.1 dB. Lines #000 and #004 acquired over similar areas have respective BS within 0.1 dB, which is within the systems precision (a calibrated fisheries echosounder is expected (Demer et al. 2015) to give a measurement accuracy of 0.1 dB). Likewise, Lines #001 and #005 are within 0.1 dB. On the “Medium” site, all measurements are homogeneous within 0.3 dB with BS values of − 21.2 to − 20.9 dB. This result demonstrates a consistent accuracy of reflectivity measurements from the EK60, and validates the processing method developed here.

Table 2 Mean values of EK60 backscatter measured along each line for the “Shallow” and “Medium” sites

EK60/EM 302 cross-comparison

Several sectors of the EM 302 overlap the EK60 insonified area at any time, but we only use the sector with the largest overlap with the EK60 footprint. Since the EK60 was mounted on the vessel’s starboard side, only data from the EM 302 starboard side swath can be readily compared with the EK60 measurements. To compare the backscatter from the EM 302 port side swath with that of the EK60, we use lines run in the opposite direction (Fig. 9). As a result, when comparing EK60 Line #000 with EM 302 Line #001, we use the EK60 data with the overlapping EM 302 data which comes from the port swath of Line# 001. Lines were only compared when they were run in a similar mode. In the end, we restricted the EM 302 data to sectors #2 (port side) and #4 (starboard side) for the “Shallow” and “Medium” modes, and to sectors #2 (port side) and #7 (starboard side) for the “Deep” mode. The frequencies used for each of those sectors are listed in Table 3. Impact of the frequency difference between those sectors and the EK60 will be briefly estimated in the Discussion (Sect. 4).

Table 3 Frequency of sectors used for comparison per line

Fig. 9

Gridded BS acquired from EM 302 (right) and EK60 (left) on the “Shallow” site. The EM 302 backscatter profile is only the one acquired during the NW-SE transect (line #000) whereas the EK60 shows line #000 and #001. Grid step is 5 m

Results of cross-comparison are detailed for both sites using the same EM 302 mode and are shown in Figs. 10 and 11 and summarized in Table 4.

Fig. 10

Comparison of along-track backscatter profiles between EK60 and EM 302 data from the “Shallow” site in M-CW-S. Black lines: BS measured by EK60. Green lines: BS measured by EM 302 on the same line (starboard swath). Red lines: BS measured by EM 302 on the other line (port swath)

Fig. 11

Comparison of along-track backscatter profiles of BS between EK60 and EM 302 data from the “Medium” site in M-CW-S. Black lines: BS measured by EK60. Green lines: BS measured by EM 302 on the same line (starboard swath). Red lines: BS measured by EM 302 on the other line (port swath)

Table 4 Intensity difference (in dB) between EK60 and EM 302 BS measurements

The comparisons between EK60 and EM 302 (Figs. 10 and 11 respectively for the “Shallow” and “Medium” and Table 4) are consistent for lines run in similar modes. In “Shallow” mode, and over the “Shallow” site, the mean backscatter difference between the two systems, $\varDelta _{EK-EM},$ shows 0.2 dB variation on the corresponding lines (values of 2.0 and 2.2 dB, starboard sector #4), and 0.8 dB on opposite lines (values of 1.1–1.9 dB, port sector #2). In “Medium” mode, the results show very good consistency, with $\varDelta _{EK-EM}$ estimated at 2.7 and 2.8 dB on the “Shallow” site and 3.1 and 2.7 dB on the “Medium” site, on corresponding lines (sector #4). On opposite lines (sector #2), values are 3.6 and 3.9 dB on the “Shallow” site and 3.8 and 3.5 dB on the “Medium” site.

Finally on the “Medium” site using the “Deep” mode, we obtained $\varDelta _{EK-EM}$ values of 4.6 and 4.2 dB on corresponding lines (sector #7) and 4.6 and 4.1 dB on opposite lines (sector #2). The variability of $\varDelta _{EK-EM}$ that is observed between lines is well within what could be expected for the system used (i.e. below 1.0 dB). This good stability of differences should lead to an absolute measurement of reflectivity after compensation of the offsets.

The consistency of the results across systems between the two sites using the same modes corroborates and reinforces our initial hypothesis that mean backscatter difference ($\varDelta _{EK-EM}$) is a robust measurement than can be used for MBES intensity calibration.

Discussion

The outcome of absolute calibration for any scientific sounder should be to make the system capable of collecting meaningful data in a repeatable and coherent fashion as stated in the BSWG recommendations (Brown et al. 2015; Rice et al. 2015). To achieve this, calibration should be independent of the environmental variabilities, i.e. spatial, temporal, and physical.

In this experiment we addressed the short-term temporal variably by running lines twice, the spatial variability by running the same mode on different areas, and we only partly addressed the physical variability by running the lines in both directions. However, our experiment did not include long-term temporal variability as there has been no repeat of the experiment with these systems.

Although this experiment suffers several limitations due either to its design or to the environmental conditions at the time, its success enables us to provide recommendations for a practical and low-budget calibration approach of MBES.

The cross-calibration has only been done at the nominal transmission angle of 45° using a fixed EK60 sounder pointing to the starboard side of the vessel. While this transmission angle has been identified as especially stable and representative of the backscatter values of the seafloor (Lamarche et al. 2011) it necessarily limited the comparison to that particular angle. However, we were able to derive good correlation levels of measurements on the port side using the return transects, allowing us to obtain comparisons on both sides of the swath. Ideally the reference measurements should be done at several transmission angles for the EK60, and on both sides of the swath. This could be possible using a steerable mount for the transducer.

In the computation of the EK60 backscatter response we used a first-order approximation for the beam footprint, assuming that the intersection of the beam with the flat seafloor is an ellipse (Fig. 7). We also ignored the difference in frequency between the systems, i.e 38 kHz for the EK60 and 27.5–30.5 kHz for the EM 302. While our assumption was that this difference in frequency is negligible in terms of backscatter levels, there is no simple way of evaluating the relevance of this approximation and its impact on our results, and we did not attempt any modelling. This may lead to biased results, or to inconsistencies across areas, as different frequencies may behave differently on various substrates (Lurton 2010; Cutter and Demer 2014; Weber and Ward 2015). This issue could now be investigated using the wideband EK80 split-beam echosounder to generates fixed frequencies from 35 to 45 kHz thus giving a good estimate of frequency dependence in this range, in the same manner investigated for frequencies between 170 and 250 kHz by Weber and Ward (2015). Looking at the available literature, the dependency of backscatter level in this frequency band has been investigated (McKinney and Anderson 1964; Stanic et al. 1988; Jackson et al. 1986): results are highly variable and substrate dependent. Most studies agree on a dependency of BS with frequency f formulated as $BS\propto 10\log f^x.$ McKinney and Anderson (1964) took measurements over a wide frequency band (12.5–290 kHz), incident angles from 1° to 90°, and obtained $x=1.6$ on most sand substrates, and $x=0$ for solid rock or clayey sand. Stanic et al. (1988) found x between − 0.03 and 0.2 for frequencies from 20 to 180 kHz at angles from 1° to 30°. For frequencies between 20 and 45 kHz, and incident angle of 20° on fine gravel, Jackson et al. (1986) obtained similar results (1.5 dB per octave ie. $x=0.2$). At higher frequencies (170–250 kHz band) and incident angles similar to ours, Weber and Ward (2015) found a rather weak frequency dependency on most substrates with x comprised between − 0.8 and 0.3. Based on those studies it is appropriate to assume a seafloor backscatter dependency law in $10\log f^x$ with $0\le x\le 1.5.$ This means that the impact of frequency on our measurements would be around 2.0 dB in the worst of cases ($x=1.5,$ $f_{EK60}=38.0$ kHz and $f_{EM 302}=27.5$ kHz), but most likely much lower considering that measurement were done on hard fine silty sediment (Lucieer and Lamarche 2011).

Another limitation of this experiment is the lack of repeated surveys enabling to analyse the impact of temporal variabilities in the water masses with their known effect on acoustic data. Because of the schedule constraints of the cruise, we had to restrict ourselves to a limited number of lines, all run around the same period. Therefore we have not addressed the potential temporal variability of measurements from the EK60. Those measurements should be repeated regularly in different environmental conditions to ensure consistent results with time over similar areas using the tilted EK60. Finally, our experiment was run in rough weather with ship’s pitch around ± 4°, roll at ± 8° and heave of more than 7 m of amplitude. This makes the ray-tracing and motion-compensation steps critical, and the BS measurement from the EK60 less reliable. Ideally those calibration lines should be run in fair weather and flat sea to remove this level of uncertainty from the process.

Conclusion

Despite limitations related to (1) the fixed angle of the EK60 used as reference, (2) poor weather during the experiment, and (3) approximations in the modelling, the results demonstrate the feasibility and robustness of our methodology. The experiment showed that using a well-known calibrated system such as an EK60 can give an absolute measurement of backscatter that constitutes a valid reference for the compensation curves of a multibeam echosounder. The compelling result from this study is that we were able to get similar calibration offsets from the EK60/EM 302 comparisons on different areas using the same echosounder modes. This suggests that we obtained what should be seen as an absolute calibration of the multibeam echosounder. The low cost of such an experiment makes it possible for it to be repeated frequently, in order to increase the accuracy and reliability of the results. We anticipate that in the future we will be able to conduct this type of cross-calibration prior to each survey, in the same way calibration lines are run systematically to get accurate bathymetric measurements.

Addendum

We have been made aware at time of publishing (Lurton, pers. comms.) of an error in the pulse duration used in the calculation of BS in Kongsberg multibeam systems. The nominal pulselength $T_n=1/B_{3dB}$ (where $B_{3dB}$ is the 3-dB bandwith of the pulse) was used instead of the effective pulselength $T_{eff}=1/T \int _{0}^{T_t}s_{env}(t)^2(t)dt$ (where $T_t$ is he total pulse length and $s_{env}(t)$ the pulse envelope) in the BS correction process. To account for the proper shape of envelope applied to the EM 302 pulse (Hanning window), all BS values must be shifted by + 2.7dB. While this very recent information has been formally referred to by Kongsberg Maritime and will be accounted for in all future work, it was not incorporated in our manuscript, as it came during the very last stage of the review process. This information does not affect our methodology, and does not alter in any ways our discussion. Nevertheless, it is very interesting that applying this bias decreases the intensity difference significantly between EK60 and EM 302 BS measurements (Table 4).