Abstract
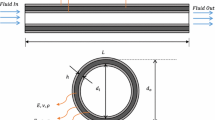
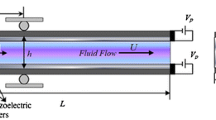
Fluid-conveying micro/Nano structures are key tools in MEMS and NEMS applications especially for drug delivery systems to attack a specific tumor like cancer cells. Vibrational characteristics of such tools play a crucial role in delivering efficient and reliable performance in various applications. As a result, vibration and instability control of such systems is of great importance. Vibration and instability response of magnetostrictive sandwich cantilever fluid-conveying micro-pipes is investigated in this paper utilizing smart magnetostrictive layers as actuators. Euler–Bernoulli beam model together with modified couple stress theory (MCST) are used to model the problem. As main properties of these smart layers, magnetic intensity effect, velocity feedback gain and thermal effects are taken into account in the modeling. The governing equation is extracted employing Hamilton’s principle. Extended Galerkin procedure is applied to discretize the governing equation and obtain the eigenvalue problem which is solved straightforwardly to reach the eigenvalues. Afterwards, eigenvalue diagrams are studied to analyze the vibrational characteristics and possible instabilities (flutter and bifurcation) occurring in first three modes of the system. Throughout this analysis, the role of various intrinsic properties of the magnetostrictive layers on the critical flow velocity and frequency is studied in detail. The numerical results show a good ability for the used smart layers to control the instability of fluid-conveying micro-pipes. Therefore, these sandwich structures may be helpful for achieving a novel design for such systems.

















Similar content being viewed by others
References
Abbasnejad, B., et al.: Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid. Microfluid. Nanofluid. 19(3), 577–584 (2015)
Ahangar, S., et al.: On the stability of a microbeam conveying fluid considering modified couple stress theory. Int. J. Mech. Mater. Des. 7(4), 327 (2011)
Amiri, A., et al.: Vibration and instability of fluid-conveyed smart micro-tubes based on magneto-electro-elasticity beam model. Microfluid. Nanofluid. 20(2), 38 (2016a)
Amiri, A., et al.: Coupled vibrations of a magneto-electro-elastic micro-diaphragm in micro-pumps. Microfluid. Nanofluid. 20(1), 18 (2016b)
Amiri, A., et al.: Wave propagation in viscous-fluid-conveying piezoelectric nanotubes considering surface stress effects and Knudsen number based on nonlocal strain gradient theory. Eur. Phys. J. Plus 133(7), 252 (2018)
Amiri, A., et al.: Flexoelectric and surface effects on size-dependent flow-induced vibration and instability analysis of fluid-conveying nanotubes based on flexoelectricity beam model. Int. J. Mech. Sci. 156, 474–485 (2019)
Arani, A.G., et al.: Strain gradient shell model for nonlinear vibration analysis of visco-elastically coupled Boron Nitride nano-tube reinforced composite micro-tubes conveying viscous fluid. Comput. Mater. Sci. 96, 448–458 (2015)
Arani, A.G., et al.: Electro-thermo-mechanical nonlinear nonlocal vibration and instability of embedded micro-tube reinforced by BNNT, conveying fluid. Physica E 45, 109–121 (2012)
Chang, T.-P., Liu, M.-F.: Small scale effect on flow-induced instability of double-walled carbon nanotubes. Eur. J. Mech. A/Solids 30(6), 992–998 (2011)
Dai, J., et al.: A parametric study on thermo-mechanical vibration of axially functionally graded material pipe conveying fluid. Int. J. Mech. Mater. Des. (2019). https://doi.org/10.1007/s10999-018-09439-5
Ebrahimi, F., Dabbagh, A.: Thermo-magnetic field effects on the wave propagation behavior of smart magnetostrictive sandwich nanoplates. Eur. Phys. J. Plus 133(3), 97 (2018)
Fathalilou, M., et al.: Stability analysis of a capacitive micro-resonator with embedded pre-strained SMA wires. Int. J. Mech. Mater. Des. (2019). https://doi.org/10.1007/s10999-018-09437-7
Ghorbanpour, A.A., et al.: Nonlinear vibration of smart micro-tube conveying fluid under electro-thermal fields. J. Solid. Mech. 4(1), 1–14 (2012)
Hong, C.: Transient responses of magnetostrictive plates by using the GDQ method. Eur. J. Mech. A/Solids 29(6), 1015–1021 (2010)
Hong, C.: Thermal vibration of magnetostrictive functionally graded material shells. Eur. J. Mech. A/Solids 40, 114–122 (2013)
Hong, C.: Thermal vibration and transient response of magnetostrictive functionally graded material plates. Eur. J. Mech. A/Solids 43, 78–88 (2014)
Hosseini, M., Bahaadini, R.: Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. Int. J. Eng. Sci. 101, 1–13 (2016)
Li, L., Hu, Y.: Critical flow velocity of fluid-conveying magneto-electro-elastic pipe resting on an elastic foundation. Int. J. Mech. Sci. 119, 273–282 (2016)
Liang, F., et al.: Transverse free vibration and stability analysis of spinning pipes conveying fluid. Int. J. Mech. Sci. 137, 195–204 (2018)
Linnemann, K., et al.: A constitutive model for magnetostrictive and piezoelectric materials. Int. J. Solids Struct. 46(5), 1149–1166 (2009)
Lotfan, S., et al.: Size-dependent nonlinear vibration analysis of carbon nanotubes conveying multiphase flow. Int. J. Mech. Sci. 115, 723–735 (2016)
Mashrouteh, S., et al.: Nonlinear free vibration analysis of a fluid-conveying microtube. In: ASME 2014 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers (2014)
Mashrouteh, S., et al.: Nonlinear vibration analysis of fluid-conveying microtubes. Nonlinear Dyn. 85(2), 1007–1021 (2016)
Ni, Q., et al.: Free vibration and stability of a cantilever beam attached to an axially moving base immersed in fluid. J. Sound Vib. 333(9), 2543–2555 (2014)
Paidoussis, M.P.: Fluid-Structure Interactions: Slender Structures and Axial Flow. Academic Press, Cambridge (1998)
Setoodeh, A., Afrahim, S.: Nonlinear dynamic analysis of FG micro-pipes conveying fluid based on strain gradient theory. Compos. Struct. 116, 128–135 (2014)
Tang, M., et al.: Nonlinear modeling and size-dependent vibration analysis of curved microtubes conveying fluid based on modified couple stress theory. Int. J. Eng. Sci. 84, 1–10 (2014)
Wang, L.: Vibration and instability analysis of tubular nano-and micro-beams conveying fluid using nonlocal elastic theory. Physica E 41(10), 1835–1840 (2009)
Wang, L., et al.: Flexural vibrations of microscale pipes conveying fluid by considering the size effects of micro-flow and micro-structure. Int. J. Eng. Sci. 71, 92–101 (2013)
Wang, Y.Q., et al.: A nonlinear surface-stress-dependent model for vibration analysis of cylindrical nanoscale shells conveying fluid. Appl. Math. Model. 64, 55–70 (2018)
Wang, Y.Q., et al.: Nonlinear dynamic characteristics of functionally graded sandwich thin nanoshells conveying fluid incorporating surface stress influence. Thin Walled Struct. 135, 537–547 (2019)
Yin, L., et al.: Strain gradient beam model for dynamics of microscale pipes conveying fluid. Appl. Math. Model. 35(6), 2864–2873 (2011)
Zhang, J., Meguid, S.: Effect of surface energy on the dynamic response and instability of fluid-conveying nanobeams. Eur. J. Mech. A/Solids 58, 1–9 (2016)
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Amiri, A., Masoumi, A. & Talebitooti, R. Flutter and bifurcation instability analysis of fluid-conveying micro-pipes sandwiched by magnetostrictive smart layers under thermal and magnetic field. Int J Mech Mater Des 16, 569–588 (2020). https://doi.org/10.1007/s10999-020-09487-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10999-020-09487-w