Size-dependent nonlinear vibration of an electrostatic nanobeam actuator considering surface effects and inter-molecular interactions

Abstract

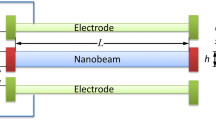
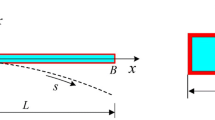
In this paper, the size-dependent nonlinear vibration of an electrostatic nanobeam actuator is investigated based on the nonlocal strain gradient theory, incorporating surface effects. A comprehensive model regarding the von Karman geometrical nonlinearity, inter-molecular forces and both components of the electrostatic excitation (AC and DC) is proposed to explore the system behavior near the primary resonance. Utilizing Hamilton’s principle, the nonlinear equation of motion of the system is derived. The natural frequency and dynamic response of the system, comprising frequency and force response diagrams, are obtained analytically via multiple scales technique in conjunction with the differential quadrature method and validated through a numerical approach. The roles of the nonlocal and strain gradient parameters, surface elasticity, inter-molecular forces and quality factor on the system oscillations are examined. The acquired results unveiled that the size-dependent parameters can significantly displace the multi-valued portions and instability thresholds of the dynamical response. Furthermore, it is deduced that the surface effects induce the stiffness hardening of the nanobeam, whereas the inter-molecular forces impose the stiffness softening effect.

Appendix

$$\begin{aligned} \begin{aligned}&{\varGamma }_1(f_1(x,t),f_2(x,t))=\zeta _1 \int _0^1 \frac{\partial f_1}{\partial x}\frac{\partial f_2}{\partial x} {\mathrm {d}}x -2 \beta ^2 \zeta _1\int _0^1 \frac{\partial ^2 f_1}{\partial x^2}\frac{\partial ^2 f_2}{\partial x^2} {\mathrm {d}}x \\&{\varGamma }_2(f_1(x,t),f_2(x,t))=-2 \beta ^2 \zeta _1\int _0^1 \frac{\partial f_1}{\partial x}\frac{\partial ^3 f_2}{\partial x^3} {\mathrm {d}}x\\&K_1(w) = \kappa _1 V_{dc}^2 \left( \frac{6\alpha ^2}{(1-w)^4}+\frac{1.3\lambda \alpha ^2}{(1-w)^3} \right) +\kappa _2\left( \frac{12\alpha ^2}{(1-w)^5}\right) +\kappa _3\left( \frac{20\alpha ^2}{(1-w)^6}\right) \\&K_2(w) = \kappa _1 V_{dc}^2 \left( \frac{2\alpha ^2}{(1-w)^3}+\frac{0.65\lambda \alpha ^2}{(1-w)^2}\right) + \kappa _2 \left( \frac{3\alpha ^2}{(1-w)^4}\right) + \kappa _3 \left( \frac{4\alpha ^2}{(1-w)^5}\right) \\&K_3(w) = \kappa _1 V_{dc}^2 \left( -\frac{1}{(1-w)^2}-\frac{0.65 \lambda }{( 1-w)}\right) + \kappa _2 \left( -\frac{1}{(1-w)^3}\right) + \kappa _3 \left( - \frac{1}{(1-w)^4}\right) . \end{aligned} \end{aligned}$$

(A.1)

$$\begin{aligned} \begin{aligned} \gamma (x)=&\left( 3{\varGamma }_1(\phi ,\phi )+3{\varGamma }_2(\phi ,\phi ) + 2{\varGamma }_1(w_s,\psi _1)+4{\varGamma }_1(w_s,\psi _2) +{\varGamma }_2(w_s,\psi _1)+2{\varGamma }_2(w_s,\psi _2)\right. \\ {}&\left. +{\varGamma }_2(\psi _1,w_s)+2{\varGamma }_2(\psi _2,w_s) \right) \left( \phi ^{(2)}-\alpha ^2 \phi ^{(4)}\right) + \left( 2{\varGamma }_1(w_s,\phi )+{\varGamma }_2(w_s,\phi )+{\varGamma }_2(\phi ,w_s) \right) \\ {}&\left( \psi _1^{(2)}+2\psi _2^{(2)} -\alpha ^2 \psi _1^{(4)}-2\alpha ^2\psi _2^{(4)} \right) + \left( 2{\varGamma }_1(\phi ,\psi _1)+4{\varGamma }_1(\phi ,\psi _2) +{\varGamma }_2(\phi ,\psi _1)+2{\varGamma }_2(\phi ,\psi _2) \right. \\&\left. +{\varGamma }_2(\psi _1,\phi )+2{\varGamma }_2(\psi _2,\phi ) \right) \left( w_s^{(2)} - \alpha ^2 w_s^{(4)}\right) -K_1(w_s) \left( 2\phi ^{(1)} \psi _1^{(1)}+4\phi ^{(1)}\psi _2^{(1)}\right) \\&-\left( K_1'(w_s) \left( 2w_s^{(1)}\left( \psi _1^{(1)}+2\psi _2^{(1)}\right) +3\left( \phi ^{(1)}\right) ^2\right) + K_2'(w_s) \left( \psi _1^{(2)}+2\psi _2^{(2)}\right) \right) \phi \\&-\left( K_1'(w_s) \left( 2w_s^{(1)}\phi ^{(1)}\right) + K_2'(w_s) \left( \phi ^{(2)}\right) \right) (\psi _1+2\psi _2) \\&-\left( K_1''(w_s) \left( 2w_s^{(1)}\phi ^{(1)}\right) + K_2''(w_s) \left( \phi ^{(2)}\right) \right) \frac{3\phi ^2}{2} \\&-\left( K_1''(w_s) \left( w_s^{(1)}\right) ^2 + K_2''(w_s) \left( w_s^{(2)}\right) + K_3''(w_s) \right) \left( \phi (\psi _1+2\psi _2)\right) \\&-\left( K_1'''(w_s) \left( w_s^{(1)}\right) ^2 + K_2'''(w_s) \left( w_s^{(2)}\right) + K_3'''(w_s) \right) \frac{\phi ^3}{2} \end{aligned} \end{aligned}$$

(A.2)

$$\begin{aligned} \begin{aligned}&-\beta ^2 \sum _{j=1}^{N}A_{ij}^{(6)} \phi _{j}+\sum _{j=1}^{N}A_{ij}^{(4)} \phi _{j}-\Bigg ( \zeta _1\sum _{i=1}^{N}C_i\bigg (\sum _{j=1}^{N}A_{ij}^{(1)} w_{s_j}\bigg )^{2} -2\beta ^2 \zeta _1\sum _{i=1}^{N}C_i\bigg (\bigg (\sum _{j=1}^{N}A_{ij}^{(2)} w_{s_j}\bigg )^{2}+\sum _{j=1}^{N}A_{ij}^{(1)} w_{s_j}\cdot A_{ij}^{(3)} w_{s_j}\bigg ) \\&+\zeta _2 \Bigg ) \Bigg ( \sum _{j=1}^{N}A_{ij}^{(2)} \phi _j-\alpha ^2\sum _{j=1}^{N}A_{ij}^{(4)}\phi _j\Bigg ) \\&-\Bigg ( 2\zeta _1\sum _{i=1}^{N}C_i \sum _{j=1}^{N}\bigg (A_{ij}^{(1)} w_{s_j}\bigg )\bigg (A_{ij}^{(1)} \phi _j\bigg )- 4\zeta _1\beta ^2\sum _{i=1}^{N}C_i \sum _{j=1}^{N}\bigg (A_{ij}^{(2)} w_{s_j}\bigg )\bigg (A_{ij}^{(2)} \phi _j\bigg )-2\zeta _1\beta ^2\sum _{i=1}^{N}C_i \sum _{j=1}^{N}\bigg (A_{ij}^{(1)} w_{s_j}\bigg )\bigg (A_{ij}^{(3)} \phi _j\bigg ) \\&-2\zeta _1\beta ^2\sum _{i=1}^{N}C_i \sum _{j=1}^{N}\bigg (A_{ij}^{(3)} w_{s_j}\bigg )\bigg (A_{ij}^{(1)} \phi _j\bigg ) \Bigg ) \Bigg ( \sum _{j=1}^{N}A_{ij}^{(2)} w_{s_j} -\alpha ^2\sum _{j=1}^{N}A_{ij}^{(4)}w_{s_j}\Bigg ) \\&+K_1(w_{s_i})\Bigg (2\sum _{j=1}^{N}\bigg (A_{ij}^{(1)} w_{s_j}\bigg )\bigg (A_{ij}^{(1)} \phi _j\bigg )\Bigg ) + K_2(w_{s_i})\Bigg (\sum _{j=1}^{N}A_{ij}^{(2)} \phi \Bigg ) \\&+\Bigg ( K_1'(w_{s_i})\bigg (\sum _{j=1}^{N}A_{ij}^{(1)} w_{s_j}\bigg )^2 + K_2'(w_{s_i})\bigg (\sum _{j=1}^{N}A_{ij}^{(2)} w_{s_j}\bigg )+ K_3'(w_{s_i}) \Bigg )\phi _i=\omega ^2 \Bigg ( \phi _i-\alpha ^2\sum _{j=1}^{N}A_{ij}^{(2)} \phi _j \Bigg ). \end{aligned} \end{aligned}$$

(A.3)