Evaluation of piezoelectric energy harvester under dynamic bending by means of hybrid mathematical/isogeometric analysis

Abstract

In this paper, a novel hybrid mathematical/isogeometric analysis (IGA) scheme is implemented to evaluate the energy harvesting of the piezoelectric composite plate under dynamic bending. The NURBS-based IGA is applied to obtain the structural response exerted by the mechanical loading. The dynamic responses conveniently coupled with the governing voltage differential equations to estimate the energy harvested. The capabilities of the scheme are shown with the comparison against analytical and full electromechanical finite element results. As there is no need of fully coupled electromechanical element, the scheme provides cheaper computational cost and could be implemented with standard computational software. Thus, it gives great benefit for early design stage. Moreover, the robustness of the scheme is shown by the couple with high order IGA element which has been proven less prone to the shear locking phenomena in the literature. The computational results show greater accuracy on structural responses and energy estimation for a very thin plate compared to the couple with standard finite element method.

1 Introduction

In this paper, work on piezoelectric energy harvesting via structural vibration is presented. The numbers of the mathematical/computational model on the piezoelectric energy harvesting has been significantly grown in the past decade. One of the earliest mathematical models is a cantilevered piezoelectric under base excitation by Erturk and Inman (2008). The model provided the basis for voltage/energy harvested from a piezoelectric composite structure under mechanical vibration and has been validated with experimental results (Erturk and Inman 2009).

On the piezoelectric energy harvesting, one of the particular fields that attract constant attention is the analysis of flow-induced/aeroelastic vibration as the source of excitation (piezoaeroelastic energy harvesting). The articles by Abdelkefi (2016) and Li et al. (2016) reviewed numerous piezoaeroelastic energy harvesting models developed within the period 2000’s–2015. It can be seen from those reviews, most of the proposed mathematical/computational models were flutter-based harvester for micro-scale application. In addition, apart from the source of excitation, the modeling of the piezoelectric energy harvester nonlinear behavior is also studied in some articles (Pasharavesh et al. 2016; Stanton et al. 2010).

Flutter-based vibration attracts considerable attention due to its self-sustained oscillatory characteristic, thus providing more sustainable power output (Erturk et al. 2010). However, flutter vibration is known for its catastrophic nature. Hence it is considered not applicable as the excitation source for a general use public structure, such as civil structure or aerospace structure, i.e. bridge, transport aircraft.

In contrast with the large development of piezo-aeroelastic energy harvesting model, the analysis under normal operational loads such as low-speed wind load on civil structure or cruise and gust load on aircraft structure has received little attention. To the authors’s knowledge, there are only a few articles proposed models for gust load on wing structure (De Marqui Jr. and Maria 2010; Xiang et al. 2015; Tsushima and Su 2016; Bruni et al. 2017) . Akbar and Curiel-Sosa (2016) proposed the model for a more general condition, dynamic bending load. The model has been successfully implemented on a typical transport aircraft wingbox structure under dynamic cruise load.

Akbar and Curiel-Sosa (2016) proposed a hybrid scheme, in which conveniently coupled the piezoelectric beam voltage equation with the dynamic responses from FEM and analytical model. By means of this scheme, it is possible to implement the responses from the various computational model (not limited to finite element model) as input to the voltage equation to provide the power output estimation.

In this current paper, a novel hybrid mathematical/isogeometric analysis (IGA) scheme is presented. The main attribute of NURBS-based IGA is the ability to establish numerical engineering analysis within the same model from the computational engineering design/drawing. Thus, decreasing the cost of numerical analysis-design interface and providing more efficient computational process compared to standard finite element (Hughes et al. 2005).

The first article of IGA by Hughes et al. (2005) was followed by the development of IGA in structural vibration (Cottrell et al. 2006) and fluid-structure interactions (Bazilevs et al. 2008) which demonstrated an excellent integration with CAD software. The smoothness of NURBS-basis functions has shown a great flexibility on various fluid structure-interaction problems (Bazilevs et al. 2008). On the analysis of structural vibrations, Cottrell et al. (2006) shows that high-order NURBS-based IGA elements provided more accurate frequency spectra than standard high-order finite elements.

A unique k-refinement also exists in NURBS-IGA formulation. This strategy involves degree elevation and knot insertion to refine the spaces (Hughes et al. 2005). Standard p-refinement as in FEM adds many degree of freedoms to the overall system, while k-refinement add fewer degree of freedoms yet still manages to obtain a higher order functions. It is also found that the k-version of IGA has better approximation properties per degree of freedom compared to the standard FEM (Evans et al. 2009).

In addition, the ease to construct high order and continuous basis functions provided interesting alternatives on solving high-order PDE problems, i.e., IGA for high-order gradient elasticity (Fischer et al. 2011; Khakalo and Niiranen 2017). Moreover, it is also found that higher-order NURBS-based IGA elements are less prone to the effect of mesh distortion (Lipton et al. 2010). Interested readers are referred to the article by Nguyen et al. (2015) for more detailed review of advantageous and disadvantageous/limitation of IGA.

In this paper, the advantage of IGA against shear locking phenomena on a thin shells and its effect on the energy harvesting response is focused. A study by Thai et al. (2012) shown that high-order IGA elements are hardly suffer from shear locking phenomena. The shear locking phenomena have been investigated since the early development of finite elements. It happens when the shear energy becomes very dominant compared to the bending energy as the thickness of the element is very small compared to its length (Kwon and Bang 2000).

Thai et al. (2012) investigated the benefits of NURBS-based IGA implementation for the structural dynamic problems of the plate with various thickness. At very thin configuration, it was concluded that the high-order IGA elements show more resistance to the shear locking phenomena compares to the standard finite element. This attribute provides an advantage in the modelling of piezoelectric structures which commonly manufactured as thin-walled structures/plates.

As reviewed by Nguyen et al. (2015), the smoothness of NURBS basis function, plate and shell elements are more convenient to be constructed. Therefore, the development of IGA shell elements has attracted significant attention in the recent years. Application on various structural mechanic problems and combination with other methods are found in the literature. Combination of IGA with the level set method is utilized for the analysis of complicated cutout plate (Yin et al. 2015). The use of simple first shear deformation theory (FSDT) with IGA provides a shear-locking free formulation (Yu et al. 2015). Buckling and free vibration analysis of the functionally graded material (FGM) plate (Yin et al. 2017). Buckling exerted by thermal and mechanical loads combination (Yu et al. 2017). A combination of extended IGA (XIGA) and level set method for analysis on a plate with internal defects (Yin et al. 2016). In addition, free-locking high order 3D IGA element also has been developed (Lai et al. 2017a) recently.

Over the past few decades, there have been extensive studies FEM model of piezoelectric structures. One of the earliest work was reported by Allik and Hughes (1970). For the first time, the piezoelectric effect incorporated in a finite element formulation of the implementation of the tetrahedral element. Numerous works on the development of FEM model of piezoelectric materials from 1970 to 2000 were reviewed by Benjeddou (2000). Over than 100 articles with different types of elements, i.e., solid, shell and beam elements, were developed during this period. Moreover, in the recent years, several advancements, i.e., Moving Kriging technique for mesh-free method (Bui et al. 2011), implementation on Abaqus User Element subroutine (Sartorato et al. 2015), Consecutive Interpolation technique with quadrilateral elements (Bui et al. 2016b), have also provided various alternatives on the piezoelectric structure analysis.

Despite numerous developments on the piezoelectric FEM model, almost all of them were implemented for actuator and sensor problems. There are only a few articles addressed energy harvesting purpose. The FEM formulation of piezoelectric energy harvester by De Marqui Jr. et al. (2009) is one of the most cited articles amongst those few. To the author’s knowledge, piezoelectric energy harvester model using IGA has not yet been developed. Furthermore, to this date, there are only a few published works presented the development of IGA models for piezoelectric structure.

Willberg and Gabbert (2012) proposed solid NURBS-based IGA piezoelectric elements. While Phung-Van et al. (2015), developed IGA shell for laminated composite plates with piezoelectric layers employing Higher-order Shear Deformation Theory (HSDT). Those models however limited to the application of sensors and actuators. Further development of piezoelectric IGA models, can be seen in the recent articles of Bui and colleagues. NURBS-based XIGA is implemented for crack problems on piezoelectric plates (Bui 2015) and piezoelectric embedded laminated composite (Bui et al. 2016a).

In the present work, high order IGA elements and FSDT are implemented to evaluate dynamic response from the laminated piezoelectric composite. The novel scheme coupled the structural responses of IGA and the voltage differential equations is proposed herein. Numerical experiments were carried out on the piezoelectric composite plate with various thickness. The discussion of the results and validation of the scheme are presented in some details.

2 Piezoelectric Energy harvester model

In this section, an introduction to the hybrid mathematical/computational piezoelectric energy harvester model is presented. Constitutive equations of piezoelectric materials in the strain-charge form is adopted in the model. The constitutive equation in this form is written as follows (Standards Committee of the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society 1988)

$$\begin{aligned} D= \varepsilon E+dT \end{aligned}$$

(1)

$$\begin{aligned} S= dE+sT \end{aligned}$$

(2)

where D, $\varepsilon$, E, T, s and S are the electrical displacement (C/m$^2$), permittivity (F/m), electrical field (V/m), mechanical stress (N/m$^2$), compliance (m$^2$/N) and mechanical strain of the material. The piezoelectric charge constant, d (m/V), denotes The coupling of the mechanical and electrical domain. It relates how much an electrical load, i.e., voltage, affect the mechanical deformation and vice versa.

The case of dynamic bending motion is considered, hence

• 1. The electrical field only generated in z-direction $E1=E2=0\ \text{and}\ E3\ne 0$;

• 2. Only one mechanical stress components generated in the x-direction $T2=$ ... $T6=0\ \text{and}\ T1\ne 0$;

• 3. All active layers are driven by the same voltage along z-direction, U3.

Therefore, Eqs. (1) and (2) become

$$\begin{aligned} D_{3}= \varepsilon _{33}E_{3}+d_{31}T_{1} \end{aligned}$$

(3)

$$\begin{aligned} S_{1}= d_{31}E_{3}+s_{11}T_{1} \end{aligned}$$

(4)

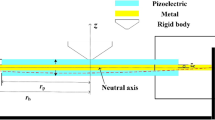
The coordinate system adopted for the piezoelectric energy harvester structure is shown in Fig. 1. The structure made of two parts, the substrate/host layers (non-piezoelectric) and the electrically active layers (piezoelectric).

Fig. 1

A cantilevered piezoelectric composite energy harvester exerted by the bending and electrical resistance load

Figure 1 shows a mechanical bending moment, M (Nm), is applied to the cantilever structure as well as the electrical resistance load, R (Ohm, Ω). Transverse displacement, Z, and bending slope, ${\partial Z }/{\partial x}$, are generated. In the active layer, the electrical field, E, and the electrical voltage, U, are created due to the structural displacement.

An important aspect here for the piezoelectric structure is that the displacement, Z, is the combination of the displacement due to the mechanical load, $Z_{mech}$, and the electrical load, $Z_{elec}$.

$$\begin{aligned} \frac{\partial Z}{\partial x}= \frac{\partial Z_{mech}}{\partial x}+\frac{\partial Z_{elec}}{\partial x} \end{aligned}$$

(5)

The $Z_{elec}$ is generated by the internal forces due to the reverse piezoelectric effect. If the reverse effect is not considered in the calculation, the structural responses and energy estimation will be highly inaccurate and overestimated the experimental results (Erturk and Inman 2011).

The governing voltage equation of the energy harvester is obtained by the modification of the piezoelectric actuator charge equation of Ballas (2007). The electrical charges of an actuator, Q(x), from the root until a certain point at length x, is expressed as a function of voltage input, U(x) and bending slope, ${\partial Z(x) }/{\partial x}$, with also material and geometrical properties of the beam/plate.

$$\begin{aligned} Q(x)=\frac{U(x)bx}{h}\left( {\varepsilon _{33}-\frac{d_{31}^2}{s_{11}}} \right) -\frac{{d_{31}}(h_{u}^2-h_{l}^2)b}{2s_{11}h}\frac{\partial Z(x) }{\partial x} \end{aligned}$$

(6)

where b and h are the width and thickness of the piezoelectric layer, while $h_{u}$ and $h_{l}$ are the height of upper and lower surfaces of the layer to the neutral axis.

As the dynamic load case is considered for the piezoelectric energy harvester, Eq. (6) is evaluated in a time-dependent domain, thus yields

$$\begin{aligned} Q(x,t)=\frac{U(x,t)bx}{h}\left( {\varepsilon _{33}-\frac{d_{31}^2}{s_{11}}} \right) -\frac{{d_{31}}(h_{u}^2-h_{l}^2)b}{2s_{11}h}\frac{\partial Z(x,t) }{\partial x} \end{aligned}$$

(7)

In the piezoelectric energy harvester case, the voltage is not an input, instead it is a response exerted by the mechanical load/structural displacement. The electrical load is given by implementing an external resistance load as shown in Fig. 1. Hence, the electrical circuit relationship is obtained as

$$\begin{aligned} \frac{\mathrm {d}Q(x,t) }{\mathrm {d} t}=I(x,t)=\frac{U(x,t)}{R} \end{aligned}$$

(8)

where, I is the electrical current (Ampere) and R is the resistance load (Ohm, ${\varOmega }$).

Incorporating Eq. (8) to (7) and assumes a harmonic oscillation motion,

$$\begin{aligned} Z(x,t)= \bar{Z}(x)e^{i\omega t} \end{aligned}$$

(9)

$$\begin{aligned} U(x,t)= \bar{U}(x)e^{i\omega t} \end{aligned}$$

(10)

Thus, Eq. (7) becomes

$$\begin{aligned} \frac{\bar{U}}{R}={i\omega }{\varGamma }_{1}\bar{U}-{i\omega }{\varGamma }_{2}\frac{\partial Z(x)}{\partial x} \end{aligned}$$

(11)

where $\bar{Z}$ and $\bar{U}$ are the displacement and voltage amplitudes, with $\omega$ is the mechanical load excitation frequency (rad/s). While t and i denote the time (s) and imaginary number, $\sqrt{-\,1}$, with the geometrical and material parameters are defined by

$$\begin{aligned} {\varGamma }_{1}= \frac{bx}{h}\left( {\varepsilon _{33}-\frac{d_{31}^2}{s_{11}}} \right) \end{aligned}$$

(12)

$$\begin{aligned} {\varGamma }_{2}= \frac{{d_{31}}(h_{u}^2-h_{l}^2)b}{2s_{11}h} \end{aligned}$$

(13)

The reverse piezoelectric effect in Eq. (10) is defined by the component of ${\varGamma }_2$ (Nm/V) and an admittance function, $H_{\alpha m}$ (rad/Nm). ${\varGamma }_2$ is defined to represents an internal bending moment, $M_{piezo}$, created by every unit of harvested voltage.

$$\begin{aligned} M_{piezo}={\varGamma }_{2}{U} \end{aligned}$$

(14)

$H_{\alpha m}$ is the admittance function (rad/Nm) defined to relate the displacement slope and the internal bending moment, $M_{piezo}$.

$$\begin{aligned} \frac{\partial Z_{elec}}{\partial x}=H_{\alpha m}M_{piezo} \end{aligned}$$

(15)

Incorporating Eqs. (5), (14) and (15) to Eq. (10), the governing voltage equation of the harvester is obtained as

$$\begin{aligned} \bar{U}(x)=\frac{{i\omega }{\varGamma }_{2}(x)\frac{\partial \bar{Z}_{mech}(x)}{\partial x}}{-\,\frac{1}{R}+{i\omega }{\varGamma }_{1}(x)-{i\omega }{{\varGamma }_{2}(x)}^2H_{\alpha m}(x)} \end{aligned}$$

(16)

It is obviously seen in Eq. (16) that the voltage amplitude can be calculated straightforwardly once the displacement due to mechanical loads, $\partial \bar{Z}_{mech}/{\partial x}$, and the admittance function, $H_{\alpha m}$, are known. It is worth to highlight that with only the input of material/geometrical properties, ${\varGamma }_{2}$, and the admittance function, $H_{\alpha m}$ is sufficient to represent the reverse piezoelectric effect. Further, it is explained in Sect. 5 that the admittance function can be solved analytically or numerically by applying a dummy mechanical load to the structure. Therefore, the hybrid scheme could provide significant benefits as it can be performed by any standard structural analysis software/formulation.

In addition, the maximum power generated from the harvester, $P_{max}$ (Watt), could be expressed as

$$\begin{aligned} P_{max}=\frac{\bar{U}^2}{R} \end{aligned}$$

(17)

3 NURBS and B-spline surface

In this section, the mathematical model of 2D NURBS function (NURBS surface) is described. NURBS stands for Non-Uniform Rational B-Spline, hence an introduction to B-spline surface is also presented. Following the notations used by Rogers (2001), the Cartesian or tensor product of B-spline surface is given by

$$\begin{aligned} Q(t,s)=\sum _{i=1}^{n+1}\sum _{j=1}^{m+1}B_{i,j}N_{i,k}(t)M_{j,l}(s) \end{aligned}$$

(18)

Basically, B-spline function is a set of polynomial functions in terms of the parametric values t and s with k and l orders. Q(t, s) is the position of any point on the B-spline surface as a function of bi-parametric coordinate t and s. Meanwhile, $B_{i,j}$ are the position vectors of the $n+1$ control points at t direction and $m+1$ control points at s direction. $N_{i,k}(t)$ and $M_{j,l}(s)$ are the normalized B-spline basis functions of order k at t direction and order l at s direction.

Physically, the B-spline surface function Q(t, s) represents the transformation of the real object/surface in the bi-parametric coordinate. The surface in Cartesian coordinate (x, y) is transformed into a surface that lies between t and s axes in the bi-parametric coordinate. Any points Q at the Cartesian coordinate is represented with any values of t and s.

The basis functions of the B-spline surface are defined by

$$\begin{aligned} N_{i,1}(t)= {\left\{ \begin{array}{ll} 1 &\quad \text { if }\, x_{i}\le t< x_{i+1} \\ 0 &\quad\text { otherwise } \end{array}\right. } \end{aligned}$$

(19)

$$\begin{aligned} N_{i,k}(t)= \frac{(t-x_{i})N_{i,k-1}(t)}{x_{i+k-1}-x_{i}}+\frac{(x_{i+k}-t)N_{i+1,k-1}(t)}{x_{i+k}-x_{i+1}}, \end{aligned}$$

(20)

and

$$\begin{aligned} M_{j,1}(s)= {\left\{ \begin{array}{ll} 1 &\quad\text { if }\, y_{j}\le s< y_{j+1} \\ 0 &\quad\text { otherwise } \end{array}\right. } \end{aligned}$$

(21)

$$\begin{aligned} M_{j,l}(s)= \frac{(s-y_{j})M_{j,l-1}(s)}{y_{j+l-1}-y_{j}}+\frac{(y_{j+l}-s)M_{j+1,l-1}(s)}{y_{j+l}-y_{j+1}} \end{aligned}$$

(22)

where $x_{i}$ and $y_{j}$ are the components of the knot vectors ${\mathbf {X}}$ and ${\mathbf {Y}}$, respectively. The maximum order of the basis functions equals to the number of control points ($k \le n+1$, $l \le m+1$) and the basis functions degree is one less of the order. The convention of $\frac{0}{0} = 0$ is adopted here.

Fig. 2

B-spline surface by CAD software

A control net is formed by the control points. This control net functioned as the frame in which the B-spline surface follows its shape. Practically, these control points are the ones that changed or controlled in a technical drawing process (usually using a CAD program) to construct the desired shape of objects. While the level of smoothness or fairness controlled with the number of control points or the order level.

An example of B-spline surface constructed with a CAD program, Autocad$^{\copyright }$, is shown in Fig. 2. Readers are refered to Shumaker et al. (2015), for details in NURBS or B-spline CAD modeling. Moreover, the algorithm samples of CAD’s spline model integration with finite element software, i.e. ABAQUS, can be seen in (Hammami et al. 2009; Lai et al. 2017b).

The shape and character of B-spline surface are also significantly influenced by the type of knot vectors used to construct the basis functions. The knot vectors are categorized into periodic and open type with uniformly spaced or non-uniformly spaced knot values (Rogers 2001). Periodic knot vectors contain knot values that increased from the start to the end. While open knot vectors has multiplicity at the start and at the ends equal to the order-k of the basis functions.

Example of a periodic uniform knot vector,

for $k=3$, ${\mathbf {X}} = [0, \frac{1}{6}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{5}{6}, 1]$.

Example of an open uniform knot vector,

for $k=3$, ${\mathbf {X}} = [0, 0, 0, \frac{1}{3}, \frac{2}{3}, 1, 1, 1]$.

For the non-uniformly spaced knot vectors, the knot values may have unequal spacing and/or multiple internal knot values.

Example of an open non-uniform knot vector,

$$\begin{aligned} {\mathbf {X}} = \left[ 0, 0, 0, \frac{1}{2}, \frac{1}{2}, 1, 1, 1\right] . \end{aligned}$$

Example of a periodic non-uniform knot vectors,

$$\begin{aligned} {\mathbf {X}} = \left[ 0, 0.28, 0.5, 0.72, 1\right] . \end{aligned}$$

In the case of NURBS surface, the B-spline function in Eq. (18) is rationalized by a set of weighting values, $w_{i,j}$. Thus, the NURBS surface is written as

$$\begin{aligned} R(t,s)=\frac{\sum _{i=1}^{n+1}\sum _{j=1}^{m+1}w_{i,j}B_{i,j}N_{i,k}(t)M_{j,l}(s)}{\sum _{i=1}^{n+1}\sum _{j=1}^{m+1}w_{i,j}N_{i,k}(t)M_{j,l}(s)} \end{aligned}$$

(23)

In most of the case, it is convenient to assume $w_{i,j} \ge 0$ for all i, j. In the case of all weighting values are equal to 1, the NURBS surface reduced to the standard B-spline surface. The addition of weighting values gives more flexibility to the creation of the surface. Thus, more complicated shape, i.e., circle or conic section, is conveniently constructible.

4 Isogeometric formulation for laminated composite

The isogeometric formulation for laminated composite based on First Shear Deformation Theory (FSDT) and Reissner–Mindlin Plate is presented in this section. In the isoparameteric finite element formulation, a particular point in an element is associated with the shape functions and the locations of all the nodes.

$$\begin{aligned} R(x,y)=\sum _{A=1}^{nn}\bar{N}_{A}(t ,s)R_{A}(x_{A},y_{A}) \end{aligned}$$

(24)

where R is a point in the element with coordinate (x, y). While, nn is the number of nodes in an element and $N_{A}(t ,s)$ is the shape function of a particular node, $R_{A}$, associated with the point R.

In the NURBS-based isogeometric formulation, the surface or element, is also represented by the NURBS function. Hence, the shape functions, $N_{ii}$, are associated with the basis functions and the control points of the NURBS surface (Thai et al. 2012). Considering a NURBS surface with control net $B_{A}$ and weighting value $w_{A}$, Eq. (23) is rewritten as

$$\begin{aligned} R(t,s)=\sum _{A=1}^{(n+1)\times (m+1)}\bar{N}_{A}(t,s)B_{A} \end{aligned}$$

(25)

where the shape function,

$$\begin{aligned} \bar{N}_{A}(t,s)=\frac{N_{A}(t,s)w_{A}}{w(t,s)} \end{aligned}$$

(26)

and

$$\begin{aligned} N_{A}(t,s)=N_{i,k}(t)M_{j,l}(s) \end{aligned}$$

(27)

Hence, the displacement at a particular point on the element is written as

$$\begin{aligned} {\mathbf {u}} (t,s)=\sum _{A=1}^{(n+1)\times (m+1)}{\bar{N}}_{A}(t,s){\mathbf {u}} _{A} \end{aligned}$$

(28)

where ${\mathbf {u}} = [u_{x}\; u_{y}\; u_{z}\; \theta _{xz}\; \theta _{yz}]^{T}$ is the displacement associated with 3 translational and 2 rotational degree of freedoms.

Adopting the formulation of Reissner–Mindlin plate with FSDT assumption, the shape function derivatives for membrane, bending and shear component are written as (Ochoa and Reddy 1992)

$$\begin{aligned} {\mathbf {B}} _{A}^{m}= \begin{bmatrix} \bar{N}_{A,x}&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad \bar{N}_{A,y}&\quad 0&\quad 0&\quad 0 \\ \bar{N}_{A,x}&\quad \bar{N}_{A,y}&\quad 0&\quad 0&\quad 0 \end{bmatrix}\end{aligned}$$

(29)

$$\begin{aligned} {\mathbf {B}} _{A}^{b}= \begin{bmatrix} 0&\quad 0&\quad 0&\quad \bar{N}_{A,x}&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad \bar{N}_{A,y} \\ 0&\quad 0&\quad 0&\quad \bar{N}_{A,x}&\quad \bar{N}_{A,y} \end{bmatrix}\end{aligned}$$

(30)

$$\begin{aligned} {\mathbf {B}} _{A}^{s}= \begin{bmatrix} 0&\quad 0&\quad \bar{N}_{A,x}&\quad \bar{N}_{A}&\quad 0 \\ 0&\quad 0&\quad \bar{N}_{A,y}&\quad 0&\quad \bar{N}_{A} \end{bmatrix} \end{aligned}$$

(31)

The stiffness matrix of the plate element, ${\mathbf {K}} ^{e}$, then obtained as

$$\begin{aligned} {\mathbf {K}} ^{e}=\int _{{\varOmega }^{e}}({\mathbf {B}} ^{m})^{T}{} {\mathbf {A}} _{c} {\mathbf {B}} ^{m}d{\varOmega }^{e}+\int _{{\varOmega }^{e}}({\mathbf {B}} ^{m})^{T}{} {\mathbf {B}} _{c}{} {\mathbf {B}} ^{b}d{\varOmega }^{e}+\int _{{\varOmega }^{e}}({\mathbf {B}} ^{b})^{T}{} {\mathbf {B}} _{c}{} {\mathbf {B}} ^{m}d{\varOmega }^{e}+\int _{{\varOmega }^{e}}({\mathbf {B}} ^{b})^{T}{} {\mathbf {D}} _{c}{} {\mathbf {B}} ^{b}d{\varOmega }^{e}+\int _{{\varOmega }^{e}}({\mathbf {B}} ^{s})^{T}{} {\mathbf {H}} _{c}{} {\mathbf {B}} ^{s}d{\varOmega }^{e} \end{aligned}$$

(32)

where ${\varOmega }^{e}$ is the domain of the element. The ${\mathbf {A}} _{c}$, ${\mathbf {B}} _{c}$, ${\mathbf {D}} _{c}$ and ${\mathbf {H}} _{c}$ matrices are the elastic of the laminate properties which represent the in-plane, bending-extension coupling, bending and inter-laminar shear components. These matrices often called as one set, the A-B-D-H matrices, and are the function of the material constitutive matrix and the orientation of the lamina (Barbero 2008). Furthermore, the mass matrix of the element, ${\mathbf {M}} ^{e}$, is written as

$$\begin{aligned} {\mathbf {M}} ^{e}= \int _{{\varOmega }^{e}}(\bar{N}_{A})^{T}{} {\mathbf {m}} \bar{N}_{A}d{\varOmega }^{e} \end{aligned}$$

(33)

with

$$\begin{aligned} {\mathbf {m}} = \rho \begin{bmatrix} h^{e}&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad h^{e}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad h^{e}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad {h^{e}}^3/12&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad {h^{e}}^3/12 \end{bmatrix} \end{aligned}$$

(34)

where $\rho$ and $h^{e}$ are the material density and the thickness of the element.

For the free vibration analysis, the eigenvalue problem is written as

$$\begin{aligned} \left( {\mathbf {K}} -\omega ^{2}_{n}{} {\mathbf {M}} \right) \hat{\mathbf{u }}=0 \end{aligned}$$

(35)

and for dynamic response problem,

$$\begin{aligned} \left( {\mathbf {K}} -\omega ^{2}{} {\mathbf {M}} \right) {\mathbf {u}} ={\mathbf {f}} \end{aligned}$$

(36)

where ${\mathbf {K}}$, ${\mathbf {M}}$, $\omega _{n}$, $\hat{\mathbf{u }}$ are the global stiffness matrix, global mass matrix, the natural frequency and the eigenvector. While ${\mathbf {u}}$ is the displacement vector exerted by the force vector ${\mathbf {f}}$.

5 Computational algorithm

In this section, the algorithm of the hybrid mathematical/numerical model is presented. The workflow of the computational process is shown in Fig. 3.

Fig. 3

Computational scheme of hybrid mathematical/numerical piezoelectric energy harvester model

Key procedures of the computational process are the evaluation of the deformation of the structure due to the actual mechanical load and the dummy load. The main outputs to be obtained from these procedures are as follows

• 1. The displacement slope (bending angle) function due to the actual mechanical loading, $\frac{\partial Z_{mech}}{\partial x}$. The load can be concentrated force, moment, or distributed pressure on the structure, or even a relative motion problem such as base excitation.

• 2. The admittance function of bending angle due to a unit of moment, $H_{\alpha m}$. The dummy load is given as a unit of moment on the neutral axis of the beam/plate tip. In the case of piezoelectric layers only cover part of the plate, the unit moment is given on the tip of the piezoelectric layer.

The simulation of the actual and dummy load is possible to be done employing an analytical or numerical method, or even experimental results. In Sects. 6 and 7, FEM and IGA are also applied to obtain the structural response.

The next primary process after the evaluation of the mechanical deformation is the evaluation of the energy harvested. A computational code is built using MATLAB$^{\copyright }$ to evaluate the voltage and power response based on Eqs. (16) and (17). Key inputs of the computational code are as follows

• 1. The complex conjugate value of the bending angle due to the actual mechanical loading, $\frac{\partial Z_{mech}}{\partial x}$.

• 2. The admittance function, $H_{\alpha m}$, obtained from the dummy load simulation.

• 3. Material properties and geometrical information of the structure.

• 4. Range of the resistance load, R, used on the electrical circuit.

To be noted that Eq. (16) is derived based on a uniform cross-section beam/plate. Therefore, in the case of non-uniform cross section, i.e. tapered beam, an approximation, i.e. polynomial function, is required to accommodate the change of the geometrical parameters along the span ($h_{u}(x)$, $h_{l}(x)$, b(x)).

In addition, it is worth to be highlighted, one of the main benefits of the hybrid scheme is the simplicity of its three primary processes. The two steps to simulate actual and dummy load simulation can be performed with standard structural analysis formulation/software, and the last step to calculate the voltage and power amplitude can be solved straightforwardly via Eqs. (16) and (17). Further elaborated in Sect. 6.2, the hybrid scheme could attain the same level of accuracy with faster computing time against fully coupled electromechanical FEM.

6 Validation

In this section, validation for the hybrid mathematical/numerical model is presented. The bimorph energy harvester model of Erturk and Inman (2011) under base excitation is used as analytical solution benchmark. The piezoelectric Kirchhoff plate of De Marqui Jr. et al. (2009) is used as benchmark for validation against electromechanically coupled finite element.

6.1 Validation against analytical solution

The material properties and geometry of the bimorph used for the analytical validation are shown in Table 1. The bimorph energy harvester comprised of two piezoelectric layers, each located on the bottom and top surface of the beam. The host structure is isotropic material placed between the piezoelectric layers.

Table 1 Material properties and geometry of the bimorph piezoelectric energy harvester (Erturk and Inman 2011)

The piezoelectric layers of bimorph energy harvester can be connected in series or parallel to the external resistance load. In the present work, series configuration of the bimorph is investigated. Three different methods, i.e., analytical, FEM and IGA are implemented to perform the structural dynamic analysis. Eight-noded bi-quadratic (Q8) FEM shell element, Nine-noded bi-quadratic (Q9) and 25-noded bi-quartic (Q25) IGA shell elements. Full integration points, $3\times 3$ for bi-quadratic and $5 \times 5$ for bi-quartic, are used. Computational codes are developed in MATLAB$^{\copyright }$ to perform FEM and IGA structural dynamic analysis.

Table 2 shows the comparison of the natural frequencies for the FEM and IGA are in good agreement with Erturk and Inman (2011).

Table 2 Natural frequency comparison, configuration from Table 1

The mode shapes obtained via IGA Q25 elements are depicted in Fig. 4a, b. In both FEM and IGA simulations, $2 \times 12$ elements are used, as it is already sufficient to attain accuracy close to the analytical solution. The frame of the undeformed plate is denoted by the black lines forming a rectangular shape. The eigenvectors are shown in the normalized values to its maximum values. It can be seen that Fig. 4a shows the first Bending mode, as the deflection is increased along the span with the maximum value at the tip. The second Bending mode is shown in Fig. 4b, the deflection changes direction, downward (z−) from root to around mid span and upward (z+) from around mid span to tip.

Fig. 4

a The first bending and b the second bending modes of the bimorph

In the present work, the resonance frequency is applied to the excitation frequency for both FEM and IGA dynamic response analysis. The comparison of the relative tip displacements and bending angles due to 1 $\upmu$m base excitation amplitude at the first bending frequency is shown in Table 3.

Table 3 Relative tip displacements and bending angles comparison, configuration from Table 1

Figure 5a, b depict the distribution of the vertical displacement (at z-direction) and the bending angle amplitudes along the span. The amplitudes shown are obtained via IGA Q25 elements. It is shown that the both the distribution of the vertical displacement and angle are similar with the first Bending mode. The values are increasing along the span with the maximum at the tip. To be noted that the shapes of displacement are shown in model scale, not in the true scale, for clearer visualization. The reader is referred to the color-bar for the true scale magnitude of the displacement and angle.

Fig. 5

a Vertical displacement and b bending angle amplitude of the bimorph

A separate code is also built via MATLAB$^{\copyright }$ to reconstruct Erturk-Inman’s model to obtain a quantitative comparison of the energy harvested over a range of resistance load. Figure 6a, b show the generated voltage and maximum power amplitude for a set of resistance load obtained via Erturk–Inman’s model and the present hybrid scheme.

Fig. 6

Variation of a the voltage and b the power amplitude versus resistance load of the bimorph

In Fig. 6a, b, denoted by “Present Model” are the present work results obtained via the hybrid mathematical/computational scheme. Denoted inside the brackets, “(FEM)”, “(IGA)” and “(Analytical)”, are the results of 3 different structural dynamic analysis coupled with the governing voltage function of Eq. (16). The FEM model used is of the FEM Q8 elements and the IGA model used is of the IGA Q25 elements.

The figures are in the logarithmic to logarithmic scale, where both the voltage and power amplitudes are normalized per unit of g ($9.81\,\hbox {m/s}^2$) and $\hbox {g}^2$. The amplitude value “per g” means it is divided by the ratio of base acceleration to g, i.e. base amplitude $1\,\upmu \hbox {m}$ and 185 Hz excitation equal with $1.35\, \hbox {m/s}^2$ base acceleration or 0.14 acceleration ratio. Hence, 100 V at this acceleration is equal with 714.3 “V per g”. In addition, the electrical power is normalized per unit $\hbox {g}^2$, or the power amplitude divided by the square of the acceleration ratio.

It is seen in Fig. 6a until Fig. 6b that the voltage and power amplitude from all four procedures are in good comparison and even difficult to distinguish. In the zoomed view of the plots, the “Present Model (FEM)” and “Present Model (IGA)” results are seen just slightly overestimate the results of Erturk–Inman’s model. Meanwhile, the “Present Model (Analytical)” results even in the zoomed scale are still coincide with the results of Erturk–Inman’s model. In detail, the comparison for the maximum voltage and power amplitude are given in Table 4. It can be seen that the variances are not significant (less than 2%).

Table 4 Electrical parameters comparison, configuration from Table 1

6.2 Validation against electromechanically coupled FEM

In this subsection, the investigation of energy harvested on UAV wing spar of De Marqui Jr. et al. (2009). The spar is a bimorph plate with the material properties and geometry as shown in Table 5. The piezoelectric layer is connected as series configuration, and the load source is the base excitation motion.

Table 5 Material properties and geometry of the bimorph UAV Wingspar (De Marqui Jr. et al. 2009)

In Table 5, the piezoelectric properties are shown in 3D orthotropic of the stress-charge form (Standards Committee of the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society 1988). The $c_{11}^{E},c_{12}^{E},\ldots ,c_{66}^{E}$ are the components of elastic stiffness of the mechanical constitutive relations. The $e_{31},e_{32},e_{33}$ are the components of piezoelectric charge constant.

De Marqui Jr. et al. (2009) adopted Kirchhoff plate theory to develop the electromechanically coupled finite element model of the piezoelectric energy harvester. The piezoceramic layer is assumed poled in the thickness direction thus align with the assumption used at 2. The piezoceramic layer is also assumed covered by a continuous electrode and perfectly bonded to the host-structure. It is assumed very thin and conductive electrode layers are on the top and bottom surfaces of the piezoceramic layers. Hence, it is assumed that all finite elements generate the same voltage output. Furthermore, one degree of freedom is used as the voltage output degree of freedom of each element. The interested reader is referred to De Marqui Jr. et al. (2009) for the detail of the formulation.

Rayleigh mechanical damping is used in the finite element formulation. The damping is assumed proportional to the mass and stiffness matrices with the constant of proportionality $\alpha$ and $\beta$. Thus the critical damping ratio $\zeta$ is written as

$$\begin{aligned} \zeta = \frac{\alpha }{2\omega _{n}}+\frac{\omega _{n}\beta }{2} \end{aligned}$$

(37)

where $\omega _{n}$ is the natural frequency of the structure. In the case presented in this subsection, $\alpha = 21.28\,\hbox {rad/s}$ and $\beta = 10^{-5}\,\hbox {s/rad}$ are used.

The configuration of the spar is limited to $10\%$ additional mass of the full aluminum spar mass. Therefore, a restriction of length and thickness of the piezoelectric layer, $\hbox {L}^{*} \times \hbox {h}^{*}\le 0.02723$, is applied. $\hbox {L}^{*}$ is the ratio of piezoelectric length to the total length of the beam and $\hbox {h}^{*}$ is the thickness ratio of one piezoelectric layer to the total thickness of the beam. The relationship of $\hbox {L}^{*} \times \hbox {h}^{*}$ boundary is shown in Fig. 7.

Fig. 7

Variation of the thickness ratio, h*, with the length ratio, L*, of the Spar

As the length and thickness of the piezoelectric layers and the aluminum layer are varied and not uniform along the span, thus, the analytical solution of Erturk and Inman (2008) is not applicable. Thus, in this subsection, the comparison is only applied to the hybrid model with FEM and IGA combinations. The FEM Q8 and IGA Q25 elements are used in the present case. Figure 8 shows the variation of the first Bending natural frequency and the critical damping ratio for various length ratio, $\hbox {L}^{*}$.

Fig. 8

Variation of the a natural frequency, b critical damping ratio with the length ratio of the Spar

It is seen from Fig. 8 the trends of the natural frequency and damping ratio for all three procedures are all in good comparison. The total mass of the beam is fixed at 1.1 full aluminum mass, and the cross section shape is maintained. It is, therefore, the only variation that affecting the change of the natural frequency is the composite material properties along the span.

In general, the natural frequency is decreasing from $\hbox {L}^{*} = 0.1$ to 1. However, from $\hbox {L}^{*}$ = 0.25 to 0.4 a slight increment occurs, despite it is followed by a significant drop from $\hbox {L}^{*}$ = 0.8 to 1. This trend is caused by a reduced stiffness of the piezo-aluminum composite beam as the piezoceramics layers approaches $\hbox {L}^{*} = 1$. In addition, for a benchmark, analytically the natural frequency of a full aluminum spar is 108.79 Hz.

The maximum power and the resistance load at the maximum power for various length ratio are depicted in Fig. 9a, b. All of the three procedures are also in good agreement. The maximum power increased at first and reached its highest point at $\hbox {L}^{*} = 0.225$ before it significantly drops when $\hbox {L}^{*}$ approach 1. In contrast, the resistance load at the maximum power is decreased with the increment of $\hbox {L}^{*}$.

De Marqui Jr. et al. (2009) concluded that for very thin piezoceramics, at $\hbox {L}^{*} > 0.5$, the effect of increased dynamic flexibility (decreased natural frequency, Fig. 8a) is not able to overcome the increased structural damping as shown in Fig. 8b. Therefore, although the flexibility is increased, the amplitude of the vibration is reduced. It resulted in the decrease of the power harvested as shown in Fig. 9a. This behavior is aligned with Eq. (16) in which the energy output is influenced by the displacement variation along the structural element.

Fig. 9

Variation of the a maximum power amplitude and b resistance load at the maximum power with the length ratio of the Spar

Figure 10 depicted the variation of the power amplitude with the resistance load for different length ratio. The black cross “$\times$” denoted $\hbox {L}^{*} = 1$ and the blue plus “+” denoted $\hbox {L}^{*} = 0.1$. It can be seen that the Power–Resistance curve is shifting from left to right as the $\hbox {L}^{*}$ decreased. In align with Eq. (12), thinner and longer piezoelectric layer means ${\varGamma }_{1}$ parameter is increased. Thus, the voltage function reached the asymptotic behavior at smaller resistance load.

Fig. 10

Variation of the power amplitude with the resistance load for various length ratio of the Spar obtained via the present hybrid scheme with IGA combination

In detail, the comparison of the natural frequency and maximum power obtained from the present hybrid model and the results of De Marqui Jr. et al. (2009) is presented in Tables 6 and 7. The first bending natural frequency is denoted by “F” and the maximum power is denoted by “P”. The subscripts “DMJ” and “Present” represent the results of De Marqui Jr. et al. (2009) and the ones obtained by means of the present hybrid scheme. The ${\varDelta }$ shows the variance of both procedures.

Table 6 Natural frequency and maximum power comparison of De Marqui Jr. et al.---FEM and present model (FEM)

Table 7 Natural frequency and maximum power comparison of De Marqui Jr. et al.---FEM and present model (IGA)

The comparison of The present hybrid scheme with FEM Q8 combination is provided in Table 6. It is shown that the natural frequencies and maximum power amplitude are all in good agreement with variances less than 1%. Moreover, the results of IGA Q25 couple is shown in Table 7 with also insignificant variations compared to De Marqui Jr. et al results. These results demonstrate the robustness of the present hybrid scheme, the capability to estimate energy harvested from a structure with non-uniform material properties and obtained a good level of accuracy similar to the electromechanically coupled finite element model.

A general illustration of the simulation time comparison between the hybrid scheme and fully coupled FEM is shown in Table 8. The simulation time of the UAV spar case with the full-length piezoelectric layer is observed. The hybrid scheme simulation utilizes the bi-quartic (Q25) IGA elements, and the fully coupled FEM utilizes eight-noded bi-quadratic (Q8) elements. The fully coupled FEM follows De Marqui Jr. et al. (2009) formulation, in which one additional voltage degree of freedom is added to each element. The configuration of $2\times 12$ elements are used. For both IGA Q25 elements and fully coupled FEM Q8 elements, computational codes are built and run via MATLAB$^{\copyright }$. The simulations are performed by a standard office laptop with Intel Core i7 2.4 GHz and 4 GB RAM.

Table 8 Simulation time comparison

In Table 8, “Hybrid-Present” denotes the present hybrid scheme coupled with IGA, while the full electromechanically coupled FEM of De Marqui Jr. et al. (2009) is denoted with “FEM–DMJ”. As explained in Sect. 5 and Fig. 3, the present hybrid scheme only requires three primary processes consisted of two numerical simulations for actual and dummy load, and one process to calculate voltage-power harvested. Step A denotes the non-coupled/purely mechanical loads numerical simulations performed via IGA Q25 configuration. Calculation of voltage ($\bar{U}$) and power ($P_{max}$) for N-number of resistance loads,R, is denoted by step B. Process of calculation in step B is also performed via a MATLAB$^{\copyright }$ computational code.

For “FEM–DMJ” simulation, the only step used is step C, the full electromechanically coupled finite element simulation. In step C, the resistance load and the mechanical load are both given as the excitation source on the finite elements, while both the structural deformation and voltage responses are obtained directly as the output of FEM simulation. It is assumed that for a set of N-numbers of R, N-times of simulations is required.

As shown in Table 8, step A shows fixed simulation time, $2\times 15$ s. The elapsed time for the actual load (base excitation) and the dummy load (the moment at the tip) are around 15 s each and independent to the number of R. In step B, shows an increment of computing time as the number of resistance loads is increasing. For a set of 100 variances of R, the elapsed time is less than 5 s. While for 10,000 numbers of R, around 15 s computing time is required. Therefore, in total, “Hybrid–Present” simulations require 35 s for 100 variances of R, and 45 s for 10,000 numbers of R.

In contrast, the simulation time required for “FEM–DMJ”, step C, is purely dependent on the number of R observed. For a simulation with one resistance load, it only requires less than 20 s. However, the simulation times are multiplied with N-number of R investigated. Therefore, if 100 number of R used, then 2000 s is required. Furthermore, if 10,000 number of R used, then 200,000 s or around 56 h is required. Interesting to note that to produce a plot with the level of detail such as shown in Fig. 10, a set of R from $10^{2}$ to $10^{8}\,{\varOmega }$ with 100 ${\varOmega }$ step is used. Thus, to produce this plot utilizing the present hybrid scheme only need less than 1 min, while with full electromechanically coupled FEM will require around 56 h.

The independence on the number of simulations on the hybrid scheme is beneficial especially in a preliminary/conceptual design stage, in which a faster iterative design process to obtain an optimal harvester structural design and resistance load is achievable. However, despite the higher computational cost, a full electromechanically coupled FEM may provide more details for a particular area of interests, i.e., the region near optimum resistance load. Thus, the hybrid scheme may build the fundamental sense of the best harvester design at the early design stage, while more detailed analysis may be provided by fully coupled FEM at the later design phase. Further in Sect. 7, the robustness of the present hybrid scheme with IGA combination is elaborated with very thin structural configurations.

7 Case study of plates with various thickness

As mentioned in Sect. 1, Thai et al. (2012) implemented NURBS-based IGA to investigate the shear locking phenomena on the dynamic response problems of the laminated composite plate. In this section, a new investigation on the effect of shear locking phenomena and the resistance of high-order IGA elements to the voltage and power responses of piezoelectric energy harvester is presented.

The present hybrid scheme with the combination of FEM and IGA are utilized to investigate plates with various thickness. The beam with the configuration on Table 1 is modified. The thickness of the beam is varied with h is the investigated thickness and $\hbox {h}_0$ is the original thickness on Table 1. Thus, a ratio of thickness, $\hbox {h}_0\hbox {/h}$ is defined as the non-dimensional parameter.

Fig. 11

Vertical displacement amplitude of the bimorph with $h_{0}/h = 10^{3.75}$ via 25-noded (quartic) IGA elements

Similar procedure as presented in Sect. 6.1 is implemented. FEM Q8, IGA Q9, and IGA Q25 elements are deployed. The same number of elements, $2 \times 12$ equal sized elements, is used. The thickness ratio of the beam is varied from $\hbox {h}_0/\hbox {h} = 1$ to $\hbox {h}_0/\hbox {h} = 10^{4}$. As the thickness ratio, $\hbox {h}_0/\hbox {h}$ increases, the investigated thickness becomes smaller. At $\hbox {h}_0/\hbox {h} = 10^{4}$, the length per thickness ratio of the element is more than 7000 and considered as a very thin element.

The numerical investigation results show that IGA Q9, Q25, and FEM Q8 elements are all maintained a good level accuracy at small thickness ratio. In contrast, at the larger thickness ratio, shear locking effect started influenced the FEM Q8 elements. Figures 11 and 12 show the structural dynamic response obtained via IGA Q25 and Q9 at thickness ratio, $\hbox {h}_0/\hbox {h} = 10^{3.75}$ or $\hbox {h}_0/\hbox {h} = 5600$ still at maintained the same level of accuracy with $\hbox {h}_0/\hbox {h} = 1$ (see Fig. 5a). The displacement obtained via FEM Q8 is depicted in Fig. 13. It can be seen the result of FEM Q8 started deviated, the level of displacement dropped lower than the IGA Q9 and Q25 results.

Fig. 12

Vertical displacement amplitude of the bimorph with $\hbox {h}_{0}/\hbox {h} = 10^{3.75}$ via 9-noded (quadratic) IGA elements

Fig. 13

Vertical displacement amplitude of the bimorph with $\hbox {h}_{0}/\hbox {h} = 10^{3.75}$ via 8-noded (quadratic) FEM elements

The variation of the tip displacement and tip angle with the thickness ratio are displayed in Fig. 14. The black line, red diamond, blue circle and green square are denoted the analytical results, FEM Q8, IGA Q9 and IGA Q25 results. The results of FEM Q8 started deviating from the analytical results at $\hbox {h}_0/\hbox {h} = 10^{3.5}$ or $\hbox {h}_0/\hbox {h} = 3200$ and dropped significantly at thickness ratio $10^4$. While the IGA 9 and IGA 25 results just slightly deviated at thickness ratio $10^4$.

Fig. 14

Variation of a the tip displacement and b the tip angle with the thickness ratio, $\hbox {h}_{0}/\hbox {h}$

The results are shown in Fig. 14 are aligned with the trend shown by Thai et al. (2012). For finite element results, the structural displacement is distorted further from the analytical results as the shear energy dominated within the element. At a particular thickness when the element becomes extremely thin, the plate/shell element behaves more like a plane stress element. Hence, the element is unable to be loaded by out-of-plane loading, i.e. bending load, and resulted in an unreliable response.

Fig. 15

Variation of reverse piezoelectric parameter for various thickness ratio, $h_{0}/h$

In Fig. 15 the effect of shear locking as the element becomes thinner to the reverse piezoelectric parameter is shown. In general, similar trend with Fig. 14 is obtained. For finite element result, the magnitude of the reverse piezoelectric parameter, $|i\omega {\varGamma }_{2}^2H_{\alpha m}|$, is dropped significantly towards h$_0$/h = 10$^{4}$. Figures 16 and 17 show the voltage-resistance and power-resistance curves shifted from the reference value at very thin plate.

Fig. 16

Plot voltage and power amplitude versus resistance load of the bimorph with $h_{0}/h = 10^{3.75}$

For the finite element results, at the very thin plates, the voltage response is underestimated at the range of resistance load close to short circuit ($R \rightarrow 0$). The geometrical configuration and material properties, ${\varGamma }_{1}\, \& \,{\varGamma }_{2}$, unaffected by the numerical results. However, for the finite element results at very thin plates, the reverse piezoelectric effect is decreased, thus, at the range near short circuit, the reverse piezoelectric parameter unable to overcome the 1/R parameter. Moreover, with also smaller mechanical deformation, hence the voltage response is underestimated.

On the other side, as the resistance value is close to the open circuit ($R \rightarrow \infty$), the 1/R parameter is decreased. Furthermore, As for FEM result, the reverse piezoelectric also dropped at the very thin plate, it led to the overestimated voltage response.

Fig. 17

Plot voltage and power amplitude versus resistance load of the bimorph with $h_{0}/h = 10^{4}$

Figures 16a and 17a show the voltage response is shifted further from the analytical value as the thickness ratio changed from 10$^{3.75}$ to 10$^{4}$. The maximum voltage is greater overestimated at thickness ratio 10$^{4}$. As the voltage responses are shifted, the power response are also shifted as shown in Figs. 16b and 17b. Despite the fact that the power-resistance curves of the finite element results similar to the trend of the analytical, the resistance values are overestimated.

Table 9 Electrical parameters comparison with h$_0$/h = 10$^{4}$

In detail, Table 9 presented the comparison of maximum voltage and maximum power amplitude with the resistance at maximum power for all procedures at $\hbox {h}_0/\hbox {h} = 10^{4}$. It can be seen that all of the methods are in good agreement except the one combined with FEM. Although the maximum power obtained with FEM combination is less than 5% variance (${\varDelta }$), however the resistance value at the maximum power is overestimated by 2.5 times the analytical result.

8 Conclusions

The hybrid mathematical model/Isogeometric Analysis (IGA) scheme to evaluate a cantilevered piezoelectric energy harvester under dynamic bending has been developed. The hybrid scheme has shown beneficial advantages, i.e., the simplicity of the primary processes on the use of standard structural analysis and straightforward governing voltage equation. It is shown in this paper; the hybrid scheme reduced computational cost compared to the more sophisticated electromechanically coupled finite elements. The capabilities and robustness of the procedure are demonstrated by comparison with results from the literature.

The numerical investigations focused on the shear locking resistance of the higher-order IGA elements have been performed. It is shown in this paper; the higher-order IGA elements are less prone to the shear locking phenomena. Employing higher-order IGA, the structural deformations and the energy responses are maintained at a reasonable level of accuracy even at a very thin structure. It is considered advantageous for the analysis of piezoelectric materials, in which usually manufactured as thin-walled structures.

However, as it is discussed earlier in the Introduction section, one of the gaps in the piezoelectric energy harvesting study is the lack of models for more general loading conditions and complex structure. Despite the ability of the hybrid formulation to provide analysis on various form of loads, i.e., force, pressure, base excitation, it is still limited to the dynamic bending cases. In order to obtain more general formulation, mixed mechanical loads, i.e., bending and torsion, need to be considered in the further development. Further elaboration on more complicated structural configuration, i.e., a tapered section, twisted section, may as well required. In this case, the ability of NURBS-based IGA on the integration with CAD software and complex shapes construction are worth to be explored in the future works.

Concerning higher-order NURBS-based IGA, it is found from the literature that it may have a negative effect on the computational cost. For a fixed number of unknown, higher-order NURBS-based IGA may consume more CPU time and RAM (Collier et al. 2012). Therefore, it is considered worth to be investigated in the future work the effect of the higher-order NURBS-based IGA to the overall computational cost of the present hybrid scheme. Despite in this paper, it is shown that there is no significant issue with the computing time, investigation on the more complex structure and more dense mesh may need to be performed in the future.

It is also found that the use of the mass matrices in higher-order IGA for structural vibration analysis is still not optimal (Cottrell et al. 2006). The lumped mass matrices limit the accuracy to just second order, even for higher-order of IGA elements. However, some attempts to develop novel high-order mass matrices are found in the literature (Wang et al. 2013, 2015). Those new mass matrices are proven to increase the level of accuracy. Thus, it may be used to enhance the performance of the present IGA elements.