Skip to main content
SpringerLink
Log in

Investigation of the problem of a plane axisymmetric cylindrical tube under internal and external pressures

  • Original Paper
  • Published:
International Journal of Mechanics and Materials in Design Aims and scope Submit manuscript

Abstract

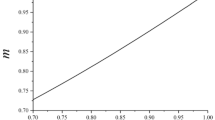
An analysis has been presented in linear elasticity for the investigation of the problem of a plane axisymmetric cylindrical tube under internal and external pressures. Stress concentration coefficients are introduced and the loci where the stress, strain and displacements fields become nul, are determined. Combinations of the lateral loads are studied and the limit values of the thickness of the tube are also examined. Applications are made for a half circle cross-tunnel and for the case of zero tensile stresses at the inner or the outer ring of a cylindrical tube.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Barber J.R.: Elasticity. Kluwer Academic Publishers, Dordrecht (1992)

    MATH  Google Scholar 

  • Filonenko-Borodich, M.: Theory of Elasticity, pp. 200–206. Mir Publishers, Moscow (1968)

    Google Scholar 

  • Gal, D., Ovorkin, J.: Stresses on anisotropic cylinders. Mech. Res. Commun. 22, 109–113 (1995)

    Article  Google Scholar 

  • Imaninejad, M., Subhash, G.: Proportional loading of thick-walled cylinders. Int. J. Pressure Vessels Piping 82, 129–135 (2005)

    Article  Google Scholar 

  • Lekhnitskii, S.G.: Anisotropic Plates, pp. 106–114. Gordon and Break Science Publishers, New York (1968)

    Google Scholar 

  • Love, A.E.H.: A Treatise on the Mathematical Theory of Elasticity. 4th ed. Cambridge University Press, Cambridge (1956)

    Google Scholar 

  • Muskhelishvili, N.I.: Some Basic Problems of the Mathematical Theory of Elasticity, 4th ed. P. Noordhoff Ltd., Groningen, The Netherlands (1963)

    MATH  Google Scholar 

  • Pilkey, D.W. (1997) Stress Concentration Factors, 2nd ed. Wiley, New York

    Google Scholar 

  • Saada, A.S.: Elasticity Theory and Applications, pp. 323–334. Pergamon Press Inc., Oxford (1979)

    Google Scholar 

  • Singh, S., Kumor, A.: Stresses due to flow past a circular cylinder. Int. J. Pressure Vessel Piping 60, 37–48 (1994)

    Article  Google Scholar 

  • Stampouloglou, I.H., Theotokoglou, E.E.: The two-actions theorem and its application to composite materials. Arch. Mech. Eng. XLIX, 297–315 (2002)

    Google Scholar 

  • Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity. McGraw-Hill Kogakusha Ltd., Tokyo (1970)

    MATH  Google Scholar 

  • Yiannopoulos, Ch.A.: A simplified solution for stresses in thick-wall cylinders for various loading conditions. Comput. Struct. 60, 571–578 (1996)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Applied Sciences, Department of Mechanics – Lab. of Strength of Materials, National Technical University of Athens, Zographou Campus, Theocaris Bld., GR-157 73, Athens, Greece

    I. H. Stampouloglou & E. E. Theotokoglou

  2. Sofouli 33, Nea Smirni, 17122, Athens, Greece

    E. E. Theotokoglou

Authors
  1. I. H. Stampouloglou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. E. Theotokoglou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. E. Theotokoglou.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stampouloglou, I.H., Theotokoglou, E.E. Investigation of the problem of a plane axisymmetric cylindrical tube under internal and external pressures. Int J Mech Mater Des 3, 59–71 (2006). https://doi.org/10.1007/s10999-006-9013-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10999-006-9013-z

Keywords

Search

Navigation