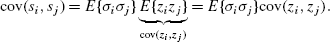Correlated topographic analysis: estimating an ordering of correlated components

Abstract

This paper describes a novel method, which we call correlated topographic analysis (CTA), to estimate non-Gaussian components and their ordering (topography). The method is inspired by a central motivation of recent variants of independent component analysis (ICA), namely, to make use of the residual statistical dependency which ICA cannot remove. We assume that components nearby on the topographic arrangement have both linear and energy correlations, while far-away components are statistically independent. We use these dependencies to fix the ordering of the components. We start by proposing the generative model for the components. Then, we derive an approximation of the likelihood based on the model. Furthermore, since gradient methods tend to get stuck in local optima, we propose a three-step optimization method which dramatically improves topographic estimation. Using simulated data, we show that CTA estimates an ordering of the components and generalizes a previous method in terms of topography estimation. Finally, to demonstrate that CTA is widely applicable, we learn topographic representations for three kinds of real data: natural images, outputs of simulated complex cells and text data.

1 Introduction

Many recent methods to analyze multidimensional data x=(x ₁,…,x _d )^⊤ are based on the linear mixing model

(1)

where A is the mixing matrix and s=(s ₁,…,s _d )^⊤ is the source vector of non-Gaussian latent variables. A special instance of (1) is independent component analysis (ICA) where all the components in s are statistically independent (Hyvärinen and Oja 2000). The goal of ICA and related methods is to estimate both A and s from observations of x only. The model (1) in ICA was proven to be identifiable up to the order, signs, and scales of the components (Comon 1994). ICA has been used in a wide range of fields such as computational neuroscience (Hyvärinen et al. 2009), natural language processing (Honkela et al. 2010) and MEG/EEG analysis (Vigário et al. 2000).

However, real data do often not follow the assumptions made in ICA. For instance, the components in s may not be statistically independent. When such components are estimated with ICA, statistical dependencies between the estimates can be observed, in violation of the independence assumption made. For natural images, for example, the conditional variance of an estimated component s _i may depend on the value of another component s _j : As |s _j | increases, the conditional variance of s _i grows. This means that the conditional distribution of s _i becomes wider as |s _j | increases, which gives the conditional histogram a characteristic bow-tie like shape (Simoncelli 1999; Karklin and Lewicki 2005). An alternative formulation of this dependency is energy correlation, $\text {cov}(s_{i}^{2},s_{j}^{2})>0$: both $s_{i}^{2}$ and $s_{j}^{2}$ tend to be co-active (Hyvärinen et al. 2009).

Therefore, it seems important to relax the independence assumption. Topographic ICA (TICA) is based on this idea (Hyvärinen et al. 2001). The key point of TICA is to arrange the components on an one- or two-dimensional grid or lattice, and allow nearby components to have energy correlations, while far-away components are assumed statistically independent. Thus, energy correlations define the proximity of the components and can be used to fix their ordering. Osindero et al. (2006) proposed another related method and their results for natural image data were similar to those obtained with TICA, although their estimations were overcomplete in contrast to the ones in TICA. Karklin and Lewicki (2005) proposed a hierarchical model where the second layer learns variance components. Further related work includes tree-like modeling of the dependencies of the components (Bach and Jordan 2003; Zoran and Weiss 2009).

The components in TICA are constrained to be linearly uncorrelated. However, uncorrelated components are not always optimal. In fact, both linear and energy correlations can be observed in many practical situations. Consider the outputs of two collinearly aligned Gabor-like filters. As natural images often contain long edges, their outputs have both linear and energy correlations (Coen-Cagli et al. 2012). Such linear correlations make the conditional histogram of the outputs have a tilted bow-tie like shape. Coherent sources in MEG or EEG data can be linearly correlated too, due to neural interactions (Gómez-Herrero et al. 2008). As we will see later, another example occurs in the analysis of text data.

In this paper, we propose a new statistical method which we call correlated topographic analysis (CTA). In CTA, topographically nearby components have linear and energy correlations, and those dependencies are used to fix the ordering as in TICA. Since CTA is sensitive to both kinds of correlations, only one kind (linear or energy) needs to exist in the data. CTA thus generalizes TICA for topography estimation.

In addition to proposing the statistical model of CTA, we propose an optimization method that performs better than standard procedures in terms of local optima. This method dramatically improves topography estimation, and we verify its performance on simulated as well as real data.

This paper is organized as follows. Section 2 motivates the estimation of topographic representations, and presents the new statistical method CTA. CTA is introduced as a special case of a more general framework which also includes ICA and TICA. In Sect. 3, we use simulated data to verify identifiability of the linear mixing model in (1) for sources with various dependency structures, and compare the performances of ICA, TICA and CTA. In Sect. 4, CTA is applied on three kinds of real data: natural images, outputs of simulated complex cells and text data. The applicability on such a wide range of data sets suggests that CTA may be widely applicable. Connections to previous work are discussed in Sect. 5. Section 6 concludes this paper.

2 Correlated topographic analysis

We start by motivating the estimation of topographic representations. Then, we introduce a generative model for the sources s in order to model ICA, TICA and CTA in a unified way, and describe the basic properties of the components in CTA. We then derive an approximation of the likelihood for CTA and propose a method for its optimization.

2.1 Motivation for estimating topographic representations

The foremost motivation for estimating topographic representations is visualization. Plotting the components with the topographic arrangement enables us to easily see the interrelationships between components. This is particularly true if the topographic grid is two dimensional and can thus be plotted on the plane.

A second motivation is that the topography learned from natural inputs such as natural images, natural sound, or text, might model cortical representations in the brain. This is based on the hypothesis that in order to minimize wiring length, neurons which interact with each other should be close to each other, see e.g. Hyvärinen et al. (2009). Minimizing wiring seems to be important to keep the volume of the brain manageable, and possibly to speed up computation as well.

An example is computation of complex cell outputs based on simple cell outputs in primary visual cortex (V1). Simple cells are sensitive to an oriented bar or an edge at a certain location in visual space, while complex cells are otherwise similar, but invariant to local sinusoidal phases of visual stimuli. Computationally, such a conversion can be achieved by pooling the squares of the outputs of the simple cells which have similar orientation and spatial location, but different phases. A topographic representation where simple cells are arranged as observed in V1 could minimize the wiring needed in such a pooling because the pooling is done over nearby cells. Such a minimum-wiring topography was found to emerge from natural images using TICA (Hyvärinen et al. 2001).

Related to minimum wiring, the topography may also enable simple definition of new, higher-order features. Summation of the features in a topographic neighborhood (possibly after a nonlinearity such as squaring) may even in general lead to interesting new features, just as in the case of simple cell pooling explained above.

2.2 The generative model

We begin with the following generative model for the latent source vector s in (1),

(2)

where ⊙ denotes element-wise multiplication, and σ=(σ ₁,…,σ _d ) and z=(z ₁,…,z _d ) are statistically independent. The two key points of the generative model (2) are the following:

• 1. If z is multivariate Gaussian with mean 0 and the elements in σ are positive random variables, which is what we assume in the following, the components in s are super-Gaussian, i.e., sparse (Hyvärinen et al. 2001).

• 2. By introducing linear correlations in z and/or energy correlations in σ, the components in s will have linear and/or energy correlations. This point will be made more precise in the following.

A special case of the model in (2) results in ICA:

Case 1:

If all the elements in z and σ are statistically independent, then s is a vector with independent sparse sources, and (2) gives the source model of ICA.

The source model of TICA can also be obtained as a special case:

Case 2:

If all the elements in z are uncorrelated, but the squares of nearby elements in σ are correlated, then s is a vector formed by sparse sources with energy correlations (and no linear correlations) within a certain neighborhood, and thus (2) gives the source model of TICA.

Here, we introduce the following two further cases:

Case 3:

If nearby elements in z are correlated, but all the elements in σ are statistically independent, then s is a sparse source vector whose elements have linear correlations (and zero or weak energy correlations) within a certain neighborhood.

Case 4:

If nearby elements in z and the squares of nearby elements in σ are correlated, then s is a sparse source vector whose elements have linear and energy correlations within a certain neighborhood, and (2) gives the source model of CTA.

The statistical dependencies of the above four cases for σ and z are summarized in Table 1.

Table 1 Dependencies of pairs of nearby elements in σ and z on four cases of sources and the corresponding source model

In the following, we concentrate on Case 4 (both energy and linear correlations). We do not explicitly consider Case 3 (linear correlations only), but we will show below with simulations that CTA identifies its sources and estimates the ordering of the components as well. This is natural since the model in Case 4 uses both linear and energy correlations to model topography, while Case 3 uses linear ones only.

2.3 Basic properties of the model

We give here basic properties of the CTA generative model (Case 4 above) and discuss the differences to TICA (Case 2). Regarding the mean, linear correlation and energy correlation in the model, the following can be shown in general:

• The mean values of all the components are zero.

  

  (3)

• Nearby components, s _i and s _j , are correlated if and only if z _i and z _j are linearly correlated. From the property (3), this is proven by

  

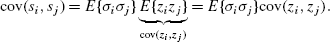  (4)

  Thus, cov(s _i ,s _j ) is the same as cov(z _i ,z _j ) up to the positive multiplication factor E{σ _i σ _j }. The linear correlation coefficient of the components has an upper bound (Appendix A).

• The energy correlation for s _i and s _j can be computed as

  

  (5)

  where we used the formula valid for Gaussian variables with zero means, $E\{z_{i}^{2}z_{j}^{2}\}=E\{z_{i}^{2}\}E\{z_{j}^{2}\}+2E\{z_{i}z_{j}\}^{2}$ which is proven by Isserlis’ theorem (Isserlis 1918; Michalowicz et al. 2009). From (5), the energy correlation is caused by the energy correlation for σ and the squared linear correlation for z. Thus, to prove that $\text {cov}(s_{i}^{2},s_{j}^{2})>0$, it is enough to prove that $\text {cov}(\sigma_{i}^{2},\sigma_{j}^{2})>0$. In the literature of TICA (Hyvärinen et al. 2001), $\text {cov}(\sigma_{i}^{2},\sigma_{j}^{2})$ is conjectured to be positive when each σ _i takes the following form,

  

  (6)

  where N(i) is an index set to determine a certain neighborhood, ϕ _i (⋅) denotes a monotonic nonlinear function and u _i is a positive random variable. We follow this conjecture. The energy correlation coefficient of the components has also an upper bound (Appendix A).

The same analysis has been done for the TICA generative model (Case 2) in Hyvärinen et al. (2001). In the model, the sources are linearly uncorrelated, and, regarding energy correlation, only the first term in (5) is nonzero because the elements in z are statistically independent. Thus, compared to TICA, in CTA, there exist linear correlations and the energy correlations are stronger as well.

2.4 Probability distribution and its approximation

We derive here a probability distribution for s to estimate the CTA generative model. We make the assumption that the precision matrix Λ of z takes a tridiagonal form, and thus, the distribution of z is given by

(7)

where the boundary of z _i is ringlike, i.e., z _i±d =z _i . All the diagonal elements in Λ are 1, the (i,i+1)-th elements are denoted by λ _i and the others are 0. For σ, we suppose that each element is given by

(8)

where u _i and v _i are independent positive random variables and statistically independent from each other. Such a mixture of u _i−1 and u _i creates energy correlations in the source vector s, while v _i generates a source-specific variance. By assuming (8), we follow the conjecture in TICA that energy correlations are positive, as in (6). We assume inverse Gamma distributions for u and v,

(9)

The a _i and b _i are positive scale parameters. If a scale parameter approaches zero, the corresponding variable converges to zero in the sense of distribution. For example, if b _i →0 for all i, the u _i approach zero, which decouples the σ _i from each other. A sketch of the process which generates the sources s and data x is depicted in Fig. 1.

Fig. 1

A sketch of the process generating data x. Adjacent elements of z are not statistically independent

Inserting (2) into (7) gives the conditional distribution for s given σ,

(10)

We show in Appendix B that Eq. (8) transforms (10) as

(11)

To obtain the distribution for s, we need to integrate out u and v in (11) using (9) as prior distributions. However, this seems to be intractable. Therefore, we resort to two approximations,

(12)

(13)

where c _i and d _i are two unknown positive scaling parameters which do not depend on u and v. The above approximations are similar to what has been done for TICA (Hyvärinen et al. 2001, Eq. (3.7)). Below we analyze the implications of these approximations. With (12) and (13), an approximation of (11) is

(14)

where we dropped terms not depending on s,v, or u. The additional parameters c _i from (12) do not affect the functional form of the approximation. The parameters d _i from (13) and λ _i occur only as a product. We thus replace them by the new parameter ϱ _i =λ _i d _i . By calculating the integral over u and v, see Appendix C for details, we obtain the following approximation for the probability distribution of s,

(15)

We use the proportionality sign because we do not know the partition function which normalizes $\tilde{p}(\mathbf {s};\boldsymbol{\varrho},\mathbf {a},\mathbf {b})$.

The approximation in (15) relates to ICA, TICA, and CTA as follows: In the limit where b _i →0, $\tilde{p}$ becomes the Laplace distribution, as often used in ICA with sparse sources (Case 1). In the limit where a _i →0 and ϱ _i =0 for all i, we obtain TICA (Case 2). Using the fixed values a _i =b _i =1 and ϱ _i =−1, we obtain

(16)

which serves as approximative distribution for the CTA model (Case 4) with positively correlated sources, as we justify in more detail below. Note that this distribution has been previously used as a prior for the regression coefficients in the fused lasso for supervised learning (Tibshirani et al. 2005). However, our application on modeling latent variables is very different.

2.5 Accuracy of the approximation

The two approximations (12) and (13) were used to derive (16). To analyze the implications of these approximations, we compared (16) with the generative model in (2) in terms of correlation and sparsity of the sources.

For the comparison, we sampled from (2) using d=2 sources and the fixed values a _i =b _i =1 for different values of λ _i =λ. We sampled from (16), with d=2, using slice sampling.¹ For both models, we drew 10⁶ samples to compute the correlation coefficient between the two sources, the correlation coefficient between their squared values, and their kurtosis.

Figure 2 shows the correlation coefficients for (2) as a function of λ (curves with solid lines), and the correlation coefficients for the approximation (16) as dashed horizontal lines. The plot suggests that the approximation has qualitatively similar correlation coefficients as the generative model for a λ close to −1.

Fig. 2

Comparing the generative model in (2) with the approximation in (16) in terms of their correlation structure. The blue and red solid curves show the correlation coefficient of the components and their squared values, respectively, for the generative model. The horizontal dashed lines show the correlation coefficients for the approximation. We find that the approximation has qualitatively similar correlation coefficients as the generative model for a λ close to −1 (Color figure online)

For the generative model, we found that the (excess) kurtosis of the sources was independent of λ, with a value around 3.4. For the approximation, we obtained a value around 2.1. This means that both the original model and the approximation yield sparse sources.

To conclude, we confirmed that the approximation has qualitatively similar properties as the generative model for a λ close to −1. The limitations of the approximation are that the sources are more strongly energy correlated but less sparse than in the original generative model for λ close to −1.

2.6 Objective function and its optimization

Using the approximative distribution (16), we can compute the log-likelihood for x and obtain the following objective function to estimate the parameter matrix W=(w ₁,…,w _d )^⊤=A ⁻¹:

(17)

(18)

(19)

where we replaced |⋅| with G(⋅)=logcosh(⋅) for numerical reasons. The vector x(t) denotes the t-th observation of the data, t=1,2,…,T. Note that J ₁ is the log-likelihood for an ICA model and that J ₂ models the topographic part, being sensitive to the order as well as the signs of the w _i .

We now describe a method to optimize the objective function in (17) because basic gradient methods tend to get stuck in local maxima as we will see in the next section. The proposed algorithm includes the following three steps:

The final output of the algorithm is W ⁽³⁾. Step 1 corresponds to performing ICA, and Step 2 gives the optimal order and the optimal signs of the ICA components in the sense of the objective function J ₂. In Step 3, W ⁽²⁾ is used as initial value of W. Therefore, Step 1 and Step 2 can be interpreted as a way to find a good initial value.

In Step 2, we have to solve a combinatorial optimization problem, which is computationally very difficult. However, we can see that the problem (21) has a nestedness property, in other words, we can divide the main problem into subproblems. So we can efficiently solve it. For example, suppose c ₁=1 and k ₁=1. When we want to find the optimal c ₂ and k ₂ given these c ₁ and k ₁, we end up with solving a smaller subproblem, which is to maximize the two terms, $f_{2}(k_{3},c_{3})=\arg\max_{k_{2},c_{2}} [-\frac{1}{T}\sum_{t=1}^{T} \{G(s^{(1)}_{1}-c_{2}s^{(1)}_{k_{2}}) +G(c_{2}s^{(1)}_{k_{2}}-c_{3}s^{(1)}_{k_{3}}) \} ]$ because the other terms do not include k ₂ and c ₂. Then, we can reuse f ₂(k ₃,c ₃) in finding the optimal c ₃ and k ₃. Under this situation, dynamic programming (DP) (Bellman 1957; Bellman and Dreyfus 1962; Held and Karp 1962) is one efficient optimization method. The description of the resulting DP algorithm is as follows:

The last term in the right-hand side of (26) was added because of the ring-like boundary. The MATLAB package of CTA by which several results presented in this paper can be reproduced is available at http://www.cs.helsinki.fi/u/ahyvarin/code/cta.

We now briefly describe the run-time cost of the optimization. When data is high-dimensional, most of the time is spent on the dynamic programming part (Algorithm 2). The computation of (23) is T times additions, and the additions are repeated 4(d−i+1)(d−i) times to make the i-th table (24). This means that the computational cost for addition is approximately $O(4T\sum_{i=2}^{d-1}(d-i+1)(d-i))=O(Td^{3})$. Thus, as the dimension of the data increases, more computational time is needed. But, as we will see below, this algorithm dramatically improves results in terms of topography estimation.

3 Identifying simulated sources

In this section, we investigate how the objective function in (17) can be used to estimate the model (1) with sources generated according to the four cases outlined in the previous section, and compare the performances of ICA, TICA and CTA.

3.1 Methods

We generated sources s according to the four cases of (2). We sampled z from a Gaussian distribution with mean 0 and covariance matrix C: In Case 3 and Case 4, all the diagonal elements are 1, the (i,i+1)-th element c _i,i+1(=c _i+1,i ) is 0.4 with a ring-like boundary, and the other elements are 0. In Case 1 and Case 2, C is the identity matrix. For σ, each element in Case 2 and Case 4 is generated as σ _i =r _i−1+r _i +r _i+1 where r _i is sampled from the exponential distribution with mean 1. In Case 1 and Case 3, σ _i =r _i . After generating s, the mean and variance of all the components s _i are standardized to zero and one, respectively. The dimension of s and the number of samples are d=20 and T=30,000, respectively.

For the generated sources of Case 3, we verified that the energy correlation was very weak: the mean of the energy correlation coefficient in $s_{1}^{2}$ and $s_{2}^{2}$ and its standard deviation in 100 source sets were 0.0192 and 0.0102, respectively.

Then, the data x was generated from the model (1) where the elements of A were randomly sampled from the standard normal distribution. The preprocessing consisted of whitening based on PCA.

For the estimation of ICA, we perform only Step 1 in Sect. 2.6. For TICA, Step 1 is performed as in CTA, but the objective functions in Step 2 and Step 3 are replaced by

(27)

In Step 2 for TICA, we do not optimize the signs of the components because (27) is insensitive to the change of signs. However, we do optimize the ordering using DP, and thus the TICA algorithm used here is an improved version of the original algorithm by Hyvärinen et al. (2001) in terms of topography estimation.

We visualize the estimation results by showing the performance matrix P=WA. If the estimation of the ordering is correct, P should be close to a diagonal matrix, or a circularly shifted diagonal matrix because of the ring-like boundary.

3.2 Results

We first show the effectiveness of our three-step optimization method in optimizing J. Then, we show the results of the comparison between ICA, TICA and CTA.

3.2.1 Escaping from local maxima

To clarify the necessity of the optimization method described in Sect. 2.6, we first show the result obtained by the conjugate gradient method only, which is equivalent to performing only Step 3 with a random initial value on W. A performance matrix P for sources generated according to Case 4 is shown in Fig. 3(a). Obviously, P is different from a (shifted) diagonal matrix. This means that the order of the estimated components is almost random, and that the estimation is incorrect. To clarify the situation, we conducted an additional experiment where W was initialized with the true matrix A ⁻¹. The resulting matrix P is shown in Fig. 3(b): P is much closer to the identity matrix and a quite good estimate. Then, we compared the values of the objective function J for the two initial conditions, the numbers are shown below Fig. 3(a) and (b). The comparison shows that the bad solution was a local maximum, and that we thus need an optimization method to escape from it.

Fig. 3

Performance matrices from (a) the conjugate gradient method only, (b) the true initialization and (c) the proposed optimization method. All performance matrices are normalized by the absolute maximum value in each P, and the data are generated using Case 4 sources. The value of the objective function J(W) in (17) is denoted below each figure (Color figure online)

A simple approach to escape from local maxima would be to permute the estimated components. However, such a permutation changes the structure of the covariance matrix, and thus provides a bad fit to the model, decreasing the objective function. In fact, as can be seen in Fig. 4(a) and (b), the structure of the covariance matrices for the original source vector and its estimate in the local maximum are qualitatively similar. Instead of permuting at the end, we empirically found it useful to permute the components at the beginning, after an initial estimation with ICA. The performance matrix P=W ⁽¹⁾ A obtained by using ICA (performing only Step 1 in Sect. 2.6) is shown in Fig. 5(a). For Fig. 5(b), the order of the row vectors in W ⁽¹⁾ was manually determined so that the maximum element on each row of P is located on a (shifted) diagonal. For (c), their signs were also changed manually. A comparison of the values of J ₂, shown in Fig. 5,² indicates that changing also the signs increases the objective function. This evidence strongly suggests that we should optimize not only the order, but also signs of the components estimated by ICA. This motivates the three-step optimization method in Sect. 2.6.

Fig. 4

Covariance matrices of (a) the original components; and components estimated by (b) the conjugate gradient method only and by (c) the proposed optimization method. The components are standardized (Color figure online)

Fig. 5

(a) The performance matrix obtained by ICA. (b) The performance matrix permuted manually so that the maximum absolute value in each row is on the diagonal, and (c) the signs in the matrix are changed as well. The value of J ₂(W) in (19) is shown below each figure (Color figure online)

Figure 3(c) shows the result when the three-step optimization method is applied to our example. The performance matrix is close to a shifted identity matrix, and the value of the objective function equals the one in Fig. 3(b). This means that our estimation is performed correctly. Furthermore, note that the signs of the diagonal elements of P in Fig. 3(c) all agree. This means that CTA solves also the sign indeterminacy problem in ICA. This is impossible for TICA because the objective function (27) is insensitive to the signs of the components.

3.2.2 Comparison to ICA and TICA

Next, we perform 100 trials for each of the four cases of sources, and compare the performance of the three methods.

To quantify how well the components are estimated, we use the Amari index (AI) (Amari et al. 1996). To further investigate how well the topography was estimated, we define a topography index (TI). To compute TI, like for AI, we first normalize P in order to take the scale indeterminacy of ICA into account. After taking the absolute values of all the elements in P, each row and column is divided by its maximum value which gives the matrices |P ₁| and |P ₂|, respectively. Next, we compute the sums over all possible shifted diagonals in |P ₁| and |P ₂|, and extract the maximum values, which are denoted by S ₁ and S ₂. Examples of shifted diagonal paths along which we compute the sums are depicted in Fig. 6(a). TI is finally given by

(28)

Matrices which show the best performance, giving TI=1, are diagonal or circularly shifted diagonal ones.

Fig. 6

(a) Examples of performance matrices for ICA, TICA and CTA in the four cases of sources. The arrows in the figure represent examples of circularly shifted diagonal trajectories in the computation of the topography index. (b) and (c) depict box plots of Amari index and topography index, respectively, obtained in 100 trials. RAND in (b) and (c) gives the baseline obtained using 100 random matrices and 100 random permutation matrices, respectively. Amari index for RAND was around 250. For Amari index, smaller means better performance. For topography index, larger means better (Color figure online)

Performance matrices for one of the 100 trials are presented in Fig. 6(a). CTA shows the best performance for sources from Case 2 to Case 4 for topography estimation. TICA cannot estimate the topography for Case 3. Regarding AI (Fig. 6(b)), CTA is not as good as ICA and TICA in Case 1 and Case 2. This is presumably because CTA forces the estimated components to be correlated even if they are not. For Case 3 and Case 4, CTA shows almost the same or a better performance than ICA and TICA. Regarding TI (Fig. 6(c)), only CTA can estimate the ordering of the components in all three topographic cases (Case 2, Case 3 and Case 4). TICA cannot estimate the topography for Case 3. We conclude that CTA shows the best performance among the three methods and generalizes TICA for topography estimation. The performance of CTA is weaker in the case of sources with no linear correlations in terms of identifiability, but it is at least as good as ICA or TICA in the case of sources with linear ones.

4 Application to real data

In this section, CTA is applied to three kinds of real data: natural images, outputs of simulated complex cells in V1, and text data.

For natural images and outputs of complex cells, the objective function in (17) is extended to a two-dimensional lattice so that a component is dependent with eight adjacent components. The extended objective function is given by

(29)

(30)

(31)

where w _i,j represents the row vector in W that corresponds to the component at position (i,j) on the two-dimensional lattice. Further, $\mathbf {ds}_{i,j}^{rh} =\mathbf {w}_{i,j}^{\top} \mathbf {x}(t)-\mathbf {w}_{i,j+1}^{\top} \mathbf {x}(t)$, $\mathbf {ds}_{i,j}^{lv} =\mathbf {w}_{i,j}^{\top} \mathbf {x}(t)-\mathbf {w}_{i+1,j}^{\top} \mathbf {x}(t)$, $\mathbf {ds}_{i,j}^{ll} =\mathbf {w}_{i,j}^{\top} \mathbf {x}(t)-\mathbf {w}_{i+1,j-1}^{\top} \mathbf {x}(t)$, and $\mathbf {ds}_{i,j}^{lr} =\mathbf {w}_{i,j}^{\top} \mathbf {x}(t)-\mathbf {w}_{i+1,j+1}^{\top} \mathbf {x}(t)$ are the differences to the right horizontal, lower vertical, lower left and lower right component, respectively. The optimization method in Sect. 2.6 was modified according to this extension: we extended Step 2 for the two-dimensional lattice and used (29) as the objective function in Step 3. Details about the extension of Step 2 can be found in Appendix D.

4.1 Natural images

Here, we apply CTA to natural image patches.

4.1.1 Methods

The data x(t) are 20 by 20 image patches which are extracted from natural images.³ The total number of patches is 100,000. As preprocessing, the DC component of each patch is removed, and whitening and dimensionality reduction are performed by PCA. We retain 252 dimensions.

4.1.2 Results

The estimated basis vectors are presented in Fig. 7. Each basis vector has spatially localized, oriented and band-pass like properties as seen in previous work (Olshausen and Field 1996; Bell and Sejnowski 1997). Furthermore, there is a clear topographic organization; similar basis vectors tend to be close to each other. A similar topographic relation can be seen in TICA (Hyvärinen and Hoyer 2001).

Fig. 7

Estimated basis vectors from natural image patches

To quantify the similarity between adjacent basis vectors and clarify the difference to TICA, we fitted Gabor functions to each basis vector. The scatter plots of the fitted Gabor parameters for pairs of adjacent basis vectors are depicted in Fig. 8. Spatial locations and orientation have strong correlations (Fig. 8(a), (b) and (c)). A large portion of basis vectors prefers high frequency (Fig. 8(d)). These results show that adjacent basis vectors have similar properties. Quite similar results were obtained by TICA (Hyvärinen and Hoyer 2001). The phase parameter however shows a clear difference. Figure 8(e) shows that there seems to exist four clusters in the scatter plot for the phases. This is in contrast to TICA where there is no clear structure in the scatter plot (Hyvärinen and Hoyer 2001, Fig. 5). In fact, the phase parameters are dominantly ±π/2 (Fig. 8(f)). This result means that most of the basis vectors have odd-symmetric spatial patterns, i.e., they represent edges, instead of bars.

Fig. 8

Scatter plots of fitted Gabor parameters for pairs of adjacent basis vectors. (a) and (b) show the spatial location along x- and y-axis. (c) shows the orientation, (d) the spatial frequency and (e) the phase. (f) Histogram of the phase parameter

4.2 Simulated complex cells

Next, CTA is applied to the outputs of simulated complex cells in V1 when stimulated with natural images. ICA and its related methods have been applied to this kind of data before (Hoyer and Hyvärinen 2002; Hyvärinen et al. 2005). Our purpose here is to investigate what kind of topography emerges for the learned higher-order basis vectors.

4.2.1 Methods

The output of a complex cell x _k is computed by the energy model:⁴

(32)

(33)

where I(x,y) is a 24 by 24 natural image patch, and $W^{o}_{k}(x,y)$ and $W^{e}_{k}(x,y)$ are even and odd symmetric Gabor functions with the same parameters except for their phases. The total number of the patches is T=100,000. The complex cells are arranged on a two-dimensional 6 by 6 grid, and at each point, there are cells with four different orientations and one frequency band. The total number of cells is 6×6×4=144. The vector x is then analyzed by CTA. Preprocessing is the same as in Sect. 4.1.1. The retained PCA dimension is 100.

4.2.2 Results

The topographic map of higher-order basis vectors is shown in Fig. 9(a). We visualized the basis vector as in previous work (Hoyer and Hyvärinen 2002; Hyvärinen et al. 2005). For each basis vector, each ellipse represents the spatial extent of the oriented filters, $W^{o}_{k}(x,y)$ and $W^{e}_{k}(x,y)$, and its orientation is the orientation which a complex cell detects. In Fig. 9(b), three prominent features are highlighted, which represent long contours, end-stopping and star-like features. On the map, the three kinds of basis vectors are separated from each other and have systematic order relationships. Furthermore, nearby long contour features tend to have the same orientation.

Fig. 9

(a) Higher order basis obtained from natural images. Note that the boundary condition of the map is ring-like. (b) Prominent features in (a), which are long contours, end-stopping and star-like features. The green lines in (a) separate the star-like features from the other ones. These outlines were determined manually (Color figure online)

Next, to test if the learned features might be due to artifacts introduced by the fixed complex cell model, we performed the same experiment when I(x,y) is Gaussian noise. Such a I(x,y) was sampled from the Gaussian distribution with mean 0 and the covariance matrix equal to the one in the natural images used in Fig. 9. The map of higher order basis vectors for the noise input is depicted in Fig. 10. Star-like features are still present, but there are no long contour and end-stopping features. Therefore, we conclude that long contours, end-stopping features and the learned topography are due to the properties of natural images.

Fig. 10

Higher order basis for Gaussian noise inputs

For comparison, we performed the same experiment by TICA.⁵ The estimated higher order basis is presented in Fig. 11(a). As in Fig. 9(a), star-like features and long contours exist. However, those features are not as well topographically aligned as those in CTA. The star-like features for TICA are more scattered on the map of the higher order basis, which disturbs the map of the features that are related to the properties of natural images. For CTA, the end-stopping features and the long contours are more neatly separated from the star-like features, which makes the learned topographic map better (Fig. 9(a)). Furthermore, most of the long contours in TICA seem to be shorter than those in CTA (Fig. 9(b) and (c)). Thus, CTA estimates longer contours and a cleaner topography than TICA does.

Fig. 11

(a) Higher order basis estimated by TICA for natural image inputs. The green lines separate the star-like features from the other kind of features. Note that the boundary condition of the map is ring-like. (b, c) Three examples of vertical contours estimated by TICA and CTA (Color figure online)

4.3 Text data

Our final application of CTA is for text data. Previously, ICA has been applied to similar data. Kolenda et al. (2000) analyzed a set of documents and showed that ICA found more easily interpretable structures than the more traditional latent semantic analysis (LSA). Honkela et al. (2010) analyzed word contexts in text corpora. ICA gave more distinct features reflecting linguistic categories than LSA. We apply here CTA to this kind of context-word data. The purpose is to see what kind of inter-relationships CTA identifies between the latent categories.

4.3.1 Methods

We constructed the context-word data as in Honkela et al. (2010). First, the most frequent T=200,000 words were collected from 51,126 Wikipedia articles written in English; these are called “collected words” in what follows. Next, we listed the context words occurring among the two words before or two words after each collected word and then took the most frequent 1,000 words. For each pair of collected and context word, we computed the joint frequency, and organized the values into a matrix Y of size 1,000 by 200,000. Finally, we obtained the context-word matrix X=(x(1),x(2),…,x(T)) by transforming each element of Y as x _i (t)=log(y _i,t +1).

As preprocessing, we made the mean of each row of X zero, and standardized its variance to one. Then, the data was whitened by PCA, and the dimension of the data was reduced from 1,000 to 60. Unlike in the experiments of natural images and outputs of complex cells, we assume here an one-dimensional topography and estimate W as described in Sect. 2.6. After the estimation, the context-word data can be represented as X=AS where S is a 60 by 200,000 category-word matrix. Note that in the context of the text data, we call the rows in S “categories”.

To quantify if the words in each category are similar to those in the same and adjacent category, we compute a similarity metric between two words using WordNet (Miller 1995; Fellbaum 1998) and the natural language toolkit (NLTK) (Bird et al. 2009). WordNet is a large lexical database where words are assigned to sets of synonyms (synsets), each expressing a lexicalized concept (Miller 1995). Since WordNet contains a network of synsets, one can compute the similarity between two words based on simple measures, e.g., the distance between synsets. For the computation of the similarity, first, we picked the top 40 words in each category, that are the words with the largest |s _i (t)|. Then, we computed similarities between all possible combinations of words within categories and between adjacent ones. The words which are not assigned to synsets were omitted from this analysis. In addition, categories in which all the top 40 words had no synsets were omitted.⁶ To compute the similarity, we used the algorithm path_similarity in NLTK which is based on the shortest path. When words had more than two synsets, we computed similarities with all possible combinations of synsets and selected the maximum value. As a baseline, we computed similarities to 1,600 pairs of words which were randomly selected from 200,000 “collected words”.

4.3.2 Results

We first show examples of latent representations of words (columns of S). In Fig. 12(a), latent representations of the names of four languages peak at the same category and show large responses around the peak. A similar property can be observed for the colors in Fig. 12(b). Honkela et al. (2010) obtained similar results: semantically similar words tend to have similar latent representations. Another interesting representation is found for numbers of years. Numbers for the late 1900’s have a strong negative peak at category 11 and a positive peak at category 42 (Fig. 12(c)), while the late 1800’s have positive peak at category 42 only (Fig. 12(d)). As another example, we found semantic categories for American states (results are not shown).

Fig. 12

Latent representations of (a) languages, (b) colors, (c) late 1900’s and (d) late 1800’s. Each plot shows a column of the matrix S. The columns are 60 dimensional vectors which contain the activations of the latent categories

Regarding the relation between categories, CTA finds topographic representations where semantically similar categories are often near to each other (Table 2 and Table 3). Categories S ⁷ (7-th row of S), S ⁸ and S ⁹, represent units of time, “quantifiers” and roman numerals, respectively (left panel in Table 2). Another topographic order is for categories related to mass media (right panel in Table 2). Job titles and names are close to each other (left panel in Table 3), we found that categories for political and educational words are close to each other as well (right panel in Table 3).

Table 2 Two examples of a topographic ordering between three categories. Denoting the k-th row of the matrix S by S ^k, the words with the top ten absolute values of a S ^k are shown

Table 3 Another two examples of a topographic ordering between three categories. “undergrad.” in S ³⁸ is an abbreviation of “undergraduate”

To quantify how similar words within or between categories are, we computed the similarities between words as described above. Fig. 13 shows the mean of the top 30 similarity values at each category⁷, and the categories are sorted in descending order for visualization. For the baseline, we first performed 1,000 times runs using pairs of randomly chosen words, and then computed the similarity as done above at each run. The baseline in Fig. 13 is the mean of those 1,000 runs. In the figure, we presented two cases of results: (a-1) and (b-1) depict the results for the best CTA run in the sense of having the largest value of the objective function, while (a-2) and (b-2) are for the worst CTA run. In total, we performed nine runs with different random initial conditions. For the similarities within categories (Fig. 13(a-1) and (a-2)), all are higher than the baseline similarity for random words. This means that CTA identifies semantically meaningful categories. Figure 13(b-1) and (b-2) clearly indicate that adjacent categories in CTA tend to contain similar words. Thus, CTA not only identifies semantically meaningful categories, but furthermore, it arranges them so that adjacent categories include semantically similar words.

Fig. 13

Mean of top 30 similarity values (a) within categories and (b) between adjacent categories. For visualization, categories are sorted in descending order. (a-1) and (b-1) depict the best CTA and best TICA run in the sense of each objective function; (a-2) and (b-2) are for the worst CTA and best TICA run. RAND is the mean similarity for pairs of randomly selected words from the 200,000 collected words. For further details, we refer to the text body (Color figure online)

We performed the same experiment and analysis for TICA. The best run results are shown in Fig. 13, too. Figure 13(a) shows that CTA and TICA have almost the same curves for similarity values within categories. However, for CTA, the curve for the similarities between adjacent categories is typically higher than for TICA (Fig. 13(b)). We performed one sided t-tests to each data in the two curves of Fig. 13(b). The null hypothesis of the test is that μ ^CTA is less than μ ^TICA where μ ^CTA denotes the mean of the points forming the CTA curve in Fig. 13(b), and μ ^TICA denotes the mean for the TICA curve. Note that we did not test if the CTA curve itself is higher than the TICA one because the points in Fig. 13 are sorted only for visualization and thus, there is no particular order-relationship between the points in the two curves. For Fig. 13(b-1) and (b-2), the p-values are 0.045 and 0.162, respectively. Thus, in the best result for CTA, the difference is statistically significant at 0.05 level (Fig. 13(b-1)). Even in the worst case, the performance of CTA seems intuitively better although the difference is not statistically significant (Fig. 13(b-2)). Therefore, we conclude that CTA identifies a better topography for text data as well.

5 Discussion

First, we summarize the connections between CTA and TICA. Then, we discuss the connection to other related work.

5.1 Connection to topographic independent component analysis

Section 2 showed that TICA and CTA are closely connected. We see their source models as special instances of the generative model (2), or of the distribution in (15). The distribution (16) which we used to define the CTA objective function is obtained from (15) by fixing the parameters a _i =1, b _i =1 and ϱ _i =−1 for all i. Ideally, we would estimate all these parameters. This is however difficult because we do not know the analytical expression of the partition function in (15). Therefore, we had to leave this challenge to future work. A possible approach is to use score matching (Hyvärinen 2006) or noise-contrastive estimation (Gutmann and Hyvärinen 2012).

The foremost difference between CTA and TICA is the additional assumption of linear correlations in the source vector s. The sensitivity to linear correlation improved the topography estimations on artificial data as well as on real data as discussed in Sect. 3.2.2 and Sect. 4. A drawback of this sensitivity is that the identifiability of CTA becomes worse than ICA or TICA when the sources have no linear correlations (Fig. 6). To fix this drawback, we should estimate the amount of linear correlations. This could be achieved by estimating the ϱ _i , which is, as mentioned above, a topic that we had to leave to future work.

5.2 Connection to other related work and possible application

Structured sparsity is a concept related to topographic analysis. Mairal et al. (2011) applied dictionary learning on natural images using structured sparsity and the results were similar to TICA. The main difference is that they did not learn linearly correlated components like CTA. As discussed above, incorporating linear correlation can have advantages in topography estimation.

For natural images, Osindero et al. (2006) proposed another energy-based model which has an objective very similar to TICA, and produces similar results on natural images. Again, the difference to our method is that linear correlations between components are not explicitly modeled. Their model allows for overcomplete bases, which by necessity introduces some linear correlations. But it seems that their model still tries to minimize linear correlations instead of explicitly allowing them.

For the outputs of complex cells Hoyer and Hyvärinen (2002) first discovered long contours by applying a non-negative sparse coding method to the data. Hyvärinen et al. (2005) applied ICA to the outputs with multiple frequency bands and found long broadband contours. Comparing with our results, the main difference is the topography of the estimated features: in Fig. 9(a), similar features are close to each other, while they are randomly organized in the work cited above. The reason is that the previously used methods assume that the components are statistically independent. In addition, the end-stopping behavior that emerges for CTA was not seen in previous work.

For the results of text data, Honkela et al. (2010) applied ICA to the same kind of word data. Categories similar to ours were learned. Since Honkela and colleagues used ICA, there were no relationships between the categories. In contrast to their results, our method estimates a topographic representation where nearby categories include semantically similar words.

We have focused on learning data representations in this paper. CTA might also be useful for engineering applications. Recently, Kavukcuoglu et al. (2009) proposed an architecture for image recognition by creating a new feature through a topographic map which is learned by a method similar to TICA. Hence, we would expect that CTA is equally applicable in such tasks, with its additional sensitivity to linear correlations possibly being an advantage. However, such a study is out of scope of this paper, and we leave it to future work.

6 Conclusion

We proposed correlated topographic analysis (CTA) which is an extension of ICA to estimate the ordering (topography) of correlated components. In the proposed method, nearby components s _i are allowed to have linear and energy correlations; far-away components are as statistically independent as possible. In previous work, only higher order correlations were introduced. Our method generalizes those methods: if either linear or energy correlations in the components are present, CTA can estimate the topography. In addition, since optimization by gradient methods tends to get stuck in local maxima, we proposed a three-step optimization method which dramatically improved topography estimation.

Besides validating the properties of CTA using artificial data, we applied CTA to three kinds of real data sets: natural images, outputs of simulated complex cells, and text data. For natural images, similar basis vectors were close to each other, and we found that most basis vectors represented edges, not bars. In the experiment using the outputs of simulated complex cells, new kinds of higher-order features emerged and, moreover, similar features were systematically organized on the lattice. Finally, we showed for text data that CTA identifies semantic categories and orders them so that adjacent categories are connected by the semantics of the words which they represent.

Appendices

Appendix A: An upper bound of the linear and energy correlation coefficient

The linear correlation coefficient $\rho_{s_{i},s_{j}}^{\text{lin}}$ for s _i and s _j reveals another relationship of linear correlations in s and z as

(34)

where $\rho^{\text{lin}}_{z_{i},z_{j}}$ denotes the linear correlation coefficient for z _i and z _j , and the Cauchy-Schwartz inequality, $E\{\sigma_{i}\sigma_{j}\}^{2}\leq E\{\sigma_{i}^{2}\}E\{\sigma_{j}^{2}\}$, was applied.

The energy correlation coefficient $\rho^{\text{ene}}_{s_{i},s_{j}}$ for s _i and s _j also has an upper bound:

(35)

where $\rho^{\text{ene}}_{\sigma_{i},\sigma_{j}}$ is the correlation coefficient of the squares of σ _i and σ _j . Inequality (35) is proven below. The energy correlation of s _i and s _j is defined by

(36)

where we used the two formulas valid for Gaussian variables with zero mean, $E\{z_{i}^{2}z_{j}^{2}\}=E\{z_{i}^{2}\}E\{z_{j}^{2}\}+2E\{z_{i}z_{j}\}^{2}$ and $E\{z_{i}^{4}\}=3E\{z_{i}^{2}\}^{2}$ which are proven by Isserlis’ theorem (Isserlis 1918; Michalowicz et al. 2009). The first term in (36) gives the following inequality,

(37)

where $3E\{\sigma_{i}^{4}\}-E\{\sigma_{i}^{2}\}^{2} > 3(E\{\sigma_{i}^{4}\}-E\{\sigma_{i}^{2}\}^{2})=3E\{(\sigma_{i}^{2}-E\{\sigma_{i}^{2}\})^{2}\}$. For the second term in (36), first, using Jensen’s inequality, $E\{\sigma_{i}^{2}\}^{2}\leq E\{\sigma_{i}^{4}\}$,

(38)

By applying the Cauchy-Schwartz inequality, $E\{\sigma_{i}^{2}\sigma_{j}^{2}\}^{2}\leq E\{\sigma_{i}^{4}\}E\{\sigma_{j}^{4}\}$, to the above inequality, the second term in (36) is bounded by the square of the linear correlation coefficient in z _i and z _j :

(39)

We obtain (35) from (37) and (39).

Appendix B: Calculations for Eq. (11)

Here, we describe the details for obtaining (11). The equation before (11) is

(40)

This equation can be rewritten as

(41)

We expand g(s,u,v) as follows:

(42)

where the ring like boundary is applied. By rewriting the terms behind the first summation in (42) with respect to each u _i , we have

(43)

We obtain Eq. (11) by inserting (43) into (41),

(44)

Appendix C: Deriving the approximation $\tilde{p}(\mathbf {s};\boldsymbol{\varrho}, \mathbf {a},\mathbf {b})$

In this appendix, we give the detailed description of how to derive the probability distribution $\tilde{p}(\mathbf {s};\boldsymbol{\varrho},\mathbf {a},\mathbf {b})$ in (15).

To obtain $\tilde{p}(\mathbf {s};\boldsymbol{\varrho},\mathbf {a},\mathbf {b})$, we have to calculate the integral

(45)

To calculate this integral, we use the following formula (Andrews and Mallows 1974),

(46)

By change of variable x=y ⁻²,

(47)

The formula (47) gives (15) as

(48)

Appendix D: Optimizing components on a two-dimensional lattice

We first present the optimization algorithm. Then, we demonstrate its effectiveness using natural image data.

4.1 D.1 Algorithm

Here, we describe the optimization method on a two-dimensional lattice. Each component is denoted by s _i,j for i=1,…,d _x and j=1,…,d _y , where d _x and d _y represent the size of the lattice along with horizontal and vertical directions, respectively. For simplicity, we suppose that d _y ≤d _x . In the method, the only difference to the optimization method on an one-dimensional lattice is Step 2 and the objective function J in Step 3. Since the objective function in Step 3 is replaced by (29), we explain the algorithm in Step 2 below.

The algorithm is a straightforward extension of the case of an one-dimensional lattice. The key idea is to optimize the order and signs of components alternately along the horizontal and vertical directions. We call each such optimization a “phase” in the algorithm. A sketch of the method is depicted in Fig. 14. In each phase, each optimization problem reduces to that of the one-dimensional lattice. Therefore, we can expect to apply the method of the one-dimensional lattice with small modifications. In fact, the modifications between the methods of the one- and two-dimensional lattice are twofold: (1) one cannot use the indices selected in the former phases and (2) components are optimized at each phase while evaluating dependencies to the components already optimized in the former phases. For example, the problem at phase 3 can be formulated as

(49)

(50)

(51)

where j=2,3,…,d _x and $s^{*}_{i,j}(t)=c^{*}_{i,j}\mathbf {W}^{(1)}_{k^{*}_{i,j}}\mathbf {x}(t)$, which is an already optimized component in former steps. k _2,j in (49) must be selected from the remaining index set $\{2,\dots,d_{x}d_{y}\}\setminus\{k^{*}_{1,2},\dots, k^{*}_{1,d_{x}},k^{*}_{2,1}, \dots, k^{*}_{d_{y},1}\}$. The brief description of the algorithm is as follows:

MATLAB code can be obtained at http://www.cs.helsinki.fi/u/ahyvarin/code/cta/.

Fig. 14

The flow of the optimization method for components on a two-dimensional lattice. Black solid arrows represent the direction of the optimization, and gray dashed arrows represent the statistical dependency to the already optimized components to be evaluated in each phase. Grayed-out cells depict the components already optimized in the former phases

4.2 D.2 Effectiveness of the optimization method on natural images

We compare results for natural images obtained by the proposed optimization method and the conjugate gradient method only. The experimental methods are described in Sect. 4.1.

Basis vectors estimated by the conjugate gradient method only are presented in Fig. 15. It seems that nearby basis vectors are less similar than those in Fig. 7. The scatter plots of the Gabor parameters shown in Fig. 16 reveal that the spatial locations of adjacent basis vectors in Fig. 15 have weaker correlations than those in Fig. 8. Furthermore, the objective function from the proposed optimization method is larger than the one from the conjugate gradient method only:

• proposed method: J(W)=−233.331

• conjugate gradient method: J(W)=−233.623

Thus, the proposed optimization method on a two-dimensional lattice works better than the conjugate gradient method only.

Fig. 15

Estimated basis vectors from natural images using the conjugate gradient method only

Fig. 16

Scatter plots of Gabor parameters for the pairs of adjacent basis vectors in Fig. 15