Counterlogicals as Counterconventionals

Abstract

We develop and defend a new approach to counterlogicals. Non-vacuous counterlogicals, we argue, fall within a broader class of counterfactuals known as counterconventionals. Existing semantics for counterconventionals (developed by Einheuser (Philosophical Studies, 127(3), 459–482 (2006)) and (Kocurek et al. Philosophers’ Imprint, 20(22), 1–27 (2020)) allow counterfactuals to shift the interpretation of predicates and relations. We extend these theories to counterlogicals by allowing counterfactuals to shift the interpretation of logical vocabulary. This yields an elegant semantics for counterlogicals that avoids problems with the usual impossible worlds semantics. We conclude by showing how this approach can be extended to counterpossibles more generally.

Appendix

In this A, we establish that the impossible worlds semantics and the expressivist semantics generate the same logic over Ł, i.e., that $\vDash _{\textsf {i}} = \vDash _{\exp }$. To do this, we establish the following:

Theorem 1

• 1. For any expressivist model $\mathcal {E} = \langle W,f \rangle$ and any x ∈ I_W, there is a impossible worlds model $\mathcal {E}^{\textsf {i}} = \langle W^{\textsf {i}},P^{\textsf {i}},f^{\textsf {i}},V^{\textsf {i}} \rangle$ and a w ∈ Wⁱ such that for all ϕ ∈Ł:

  $$ \begin{array}{@{}rcl@{}} \mathcal{E},x \Vdash_{\exp} \phi & \quad{\Leftrightarrow}\quad \mathcal{E}^{\textsf{i}},w \Vdash_{\textsf{i}} \phi. \end{array} $$

  When x ∈ CI_W, we can take w ∈ Pⁱ.

• 2. For any impossible worlds model $\mathcal {I} = \langle W,P,f,V \rangle$ and any w ∈ W, there is a expressivist model $\mathcal {I}^{\exp } = \langle W^{\exp },f^{\exp } \rangle$ and an $x \in I_{W^{\exp }}$ such that for all ϕ ∈Ł:

  $$ \begin{array}{@{}rcl@{}} \mathcal{I},w \Vdash_{\textsf{i}} \phi & \quad{\Leftrightarrow}\quad \mathcal{I}^{\exp},x \Vdash_{\exp} \phi. \end{array} $$

  When w ∈ P, we can take $x \in CI_{W^{\exp }}$.

Corollary 1

For any ${\Gamma } \mathrel {\subseteq } \L$ and ϕ ∈Ł, ${\Gamma } \vDash _{\textsf {i}} \phi$ iff ${\Gamma } \vDash _{\exp } \phi$.

It is easiest to establish Theorem 1(a) first.

Proof Proof (Theorem 1(a))

Suppose first that x ∈ CI_W. Define $\mathcal {E}^{\textsf {i}} = \langle W^{\textsf {i}},P^{\textsf {i}},f^{\textsf {i}},V^{\textsf {i}} \rangle$ as follows:

• Wⁱ = I_W

• Pⁱ = W ×{c_x}

• for each y ∈ Wⁱ and $X \mathrel {\subseteq } W^{\textsf {i}}$, fⁱ(X,y) = f(X,y)

• for each y ∈ Pⁱ, Vⁱ(p,y) = 1 iff w_y ∈ c_y(p)

• for each y∉Pⁱ, Vⁱ(ϕ,y) = 1 iff $\mathcal {E},y \Vdash _{\exp } \phi$.

Clearly, $\mathcal {E}^{\textsf {i}}$ is a impossible worlds model and x ∈ Pⁱ. It suffices to show that for any ϕ and any y ∈ I_W:

$$ \begin{array}{@{}rcl@{}} \mathcal{E},y \Vdash_{\exp} \phi & \quad {\Leftrightarrow}\quad \mathcal{E}^{\textsf{i}},y \Vdash_{\textsf{i}} \phi. \end{array} $$

If y∉Pⁱ, then by construction, $\mathcal {E}^{\textsf {i}},y \Vdash _{\textsf {i}} \phi$ iff Vⁱ(ϕ,y) = 1 iff $\mathcal {E},y \Vdash _{\exp } \phi$. If y ∈ Pⁱ, then we proceed by induction. The atomic case holds by definition of Vⁱ. The other cases are straightforward since c_y = c_x is classical and since Pⁱ = W ×{c_x}.

Now suppose x∉CI_W. Then we can define $\mathcal {E}^{\textsf {i}}$ as above except now we take Pⁱ = CI_W. Then $\mathcal {E},x \Vdash _{\exp } \phi$ iff $\mathcal {E}^{\textsf {i}},x \Vdash _{\textsf {i}} \phi$ by construction of Vⁱ. □

Theorem 1(a) is not terribly surprising in retrospect. All it says is that anything that is i-valid is also $\exp$-valid. But i-validity is pretty weak without further constraints. One way to make that clear is to observe that, as far as the logic is concerned, counterfactuals behave exactly like distinct atomic sentences.

Definition 1

An Ł-formula is an S5-formula if it does not contain . An Ł-formula is a counterfactual if its main connective is .

Proposition 1

Let ${\mathscr{M}} = \langle P,i \rangle$ be an S5-model (where $i(p) \mathrel {\subseteq } P$ for all p ∈At) and let ${\Phi }:{P}\rightarrow \wp ({\mathscr{L}})$ map every w ∈ P to a set Φ_w of counterfactuals. Then there is an impossible worlds model $\mathcal {I} = \langle {W,P,f,V}\rangle$ such that for any w ∈ P:

• 1. if ϕ is an S5-formula, then $\mathcal {I},w \Vdash _{\textsf {i}} \phi$ iff ${\mathscr{M}},w \Vdash _{\textbf {S5}} \phi$

• 2. if ψ is a counterfactual, then $\mathcal {I},w \Vdash _{\textsf {i}} \psi$ iff ψ ∈Φ_w.

Proof

WLOG, we may assume that P is disjoint from Ł and from (Ł × P). Define $\mathcal {I} = \langle P \cup \L \cup (\L \times P),P,f,V \rangle$, where:

• for each p ∈At and w ∈ P, V (p,w) = 1 iff w ∈ i(p)

• for each ϕ ∈Ł and α ∈Ł, V (ϕ,α) = 1 iff α = ϕ

• for each ϕ ∈Ł and 〈α,w〉∈ (Ł × P), V (ϕ,〈α,w〉) = 1 iff

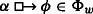
• f is any selection function with the following property: if X ∩Ł = {α} and w ∈ P, then f(X,w) = {〈α,w〉}.

It is easy to establish (i) by induction. As for (ii), note that $\llbracket {\alpha }\rrbracket ^{\mathcal {I}} \cap \L = \{\alpha \}$, so $f(\llbracket {\alpha }\rrbracket ^{\mathcal {I}},w) = \{\langle {\alpha ,w}\rangle \}$. Hence, iff $\mathcal {I},\langle {\alpha ,w}\rangle \Vdash _{\textsf {i}} \beta$, i.e., V (β,〈α,w〉) = 1, which holds iff . □

Corollary 2

Let 𝜃 be any consistent S5-formula, and let 𝜃^∗ be the result of simultaneously uniformly substituting one or more atomic sentences in 𝜃 for distinct counterfactuals. Then 𝜃^∗ is i-satisfiable.

Proof

Let ${q}_1, \dots , {q}_n$ be the atomics in 𝜃 that are substituted for distinct counterfactuals ${\psi }_1, \dots , {\psi }_n$ resulting in 𝜃^∗. Since 𝜃 is consistent, it is S5-satisfiable. Let ${\mathscr{M}},w \Vdash _{\textbf {S5}} \theta$. For each $v \in W^{{\mathscr{M}}}$, define:

$$ \begin{array}{@{}rcl@{}} {\Phi}_v \mathrel{:=} \{\psi_{i} | \mathcal{M},v \Vdash_\textbf{S5} q_i\} \end{array} $$

By Proposition 1, this guarantees us an S5-equivalent impossible worlds model $\mathcal {I}$ such that $\mathcal {I},v \Vdash _{\textsf {i}} \psi$ iff ψ ∈Φ_v where ψ is a counterfactual. Moreover, in this model, . And since $\mathcal {I},w \Vdash _{\textsf {i}} \theta$, it follows that $\mathcal {I},w \Vdash _{\textsf {i}} \theta ^{*}$. □

Corollary 2 effectively says that there are no non-trivial valid inferences governing counterfactuals in the impossible worlds semantics: any inference with counterfactuals that’s i-valid is already S5-valid.

Theorem 1(b) is harder to establish. The main issue is that while hyperconventions are allowed to redefine the semantic value of the boolean connectives, they cannot touch the semantics of . But in the impossible worlds semantics, any set of Ł-formulas is satisfied at some (perhaps impossible) world in some model, including those containing counterfactuals. Thus, if we are to establish Theorem 1(b), we need to establish the expressivist analogue of Proposition 1. Indeed, this can be done, though the proof is more involved.

Proposition 2

Let ${\mathscr{M}} = \langle W,i \rangle$ be an S5-model and let ${\Phi }:{P}\rightarrow \wp ({\mathscr{L}})$ map every w ∈ W to a set Φ_w of counterfactuals. Then there is a expressivist model $\mathcal {E} = \langle W,f \rangle$ and a classical hyperconvention c such that for any w ∈ W:

• (i) if ϕ is an S5-formula, then $\mathcal {E},w,c \Vdash _{\exp } \phi$ iff ${\mathscr{M}},w \Vdash _{\textbf {S5}} \phi$

• (ii) if ψ is a counterfactual, then $\mathcal {E},w,c \Vdash _{\exp } \psi$ iff ψ ∈Φ_w.

Proof

Since S5 is invariant under bisimulation contraction (and so, invariant under duplication of worlds), we may assume WLOG that W is infinite. We define c simply as the classical hyperconvention over W where c(p) = i(p) for all p ∈At.

We now set out to define f. Fix an arbitrary w₀ ∈ W. Let ${h}:{{\mathscr{L}}}\rightarrow {W - \{w_{0},w\}}$ be a bijection. We’ll write w_ϕ in place of h(ϕ) throughout. Now, let ${\Gamma } \subseteq \L$. Define the hyperconvention c_Γ as follows (where and $\circ \in \{\wedge ,\vee ,\rightarrow \}$):

$$ \begin{array}{@{}rcl@{}} c_{\Gamma}(p) & =& { \begin{cases} \{w_p,w_0\} & \text{if } p \in {\Gamma} \\ \{w_p\} & \text{otherwise} \end{cases}} \\ c_{\Gamma}(\star)(X) & =& { \begin{cases} \{w_{\star\phi} ~|~ w_\phi \in X\} \cup \{w_0\} & \parbox[t]{.5\textwidth}{if $\star\phi \in {\Gamma}$ whenever $w_{\phi} \in X$} \\ \{w_{\star\phi} ~|~w_\phi \in X\} & \text{otherwise} \end{cases}} \\ c_{\Gamma}(\mathrel{\circ})(X,Y) & {=}& { {{\begin{cases} \{w_{\phi \mathrel{\circ} \psi} ~|~ w_\phi \in X \text{ and } w_\psi \in Y\} \cup \{w_0\} & \parbox[t]{.35\textwidth}{if $\phi \mathrel{\circ} \psi \in {\Gamma}$ whenever $w_{\phi} \in X$ and $w_{\psi} \in Y$} \\ \{w_{\phi \mathrel{\circ} \psi} ~|~w_\phi \in X \text{ and } w_\psi \in Y\} & \text{otherwise} \end{cases}}}} \end{array} $$

Let . Define f as follows:

Let $\mathcal {E} = \langle W,f \rangle$. It is easy to check that (i) holds by induction. So we just need to establish (ii). First, some intermediate claims:

Claim 1

For any Γ and any ϕ,ψ: $\mathcal {E},w_{\phi },c_{\Gamma } \Vdash \psi$ iff ϕ = ψ.

Proof

By induction. The atomic case holds by definition of c_Γ. The cases for the connectives is straightforward. For the counterfactual, iff $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w_{\phi },c_{{\Gamma }}) \subseteq \llbracket {\beta }\rrbracket ^{\mathcal {E}}$. By induction hypothesis, $\langle {w_{\gamma },c_{{\Gamma }}}\rangle \in \llbracket {\beta }\rrbracket ^{\mathcal {E}}$ iff γ = β. Hence, $\llbracket {\beta }\rrbracket ^{\mathcal {E}} \neq I_{W}$, which means $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w_{\phi },c_{{\Gamma }}) \subseteq \llbracket {\beta }\rrbracket ^{\mathcal {E}}$ iff $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w_{\phi },c_{{\Gamma }}) = \{\langle {w_{\beta },c_{{\Gamma }}}\rangle \}$, which holds iff . But again by induction hypothesis, $\langle {w_{\alpha },c_{{\Gamma }}}\rangle \in \llbracket {\alpha }\rrbracket ^{\mathcal {E}}$. Thus, iff . □

Claim 2

For any Γ and any ϕ: $\mathcal {E},w_{0},c_{\Gamma } \Vdash \phi$ iff ϕ ∈Γ.

Proof

By induction. The atomic case holds by definition of c_Γ. The cases for the connectives is straightforward using Claim 1 and the inductive hypothesis. For the counterfactual, iff $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w_{0},c_{{\Gamma }}) \subseteq \llbracket {\beta }\rrbracket ^{\mathcal {E}}$. By Claim 1, $\langle {w_{\gamma },c_{{\Gamma }}}\rangle \in \llbracket {\alpha }\rrbracket ^{\mathcal {E}}$ iff γ = α. So $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w_{0},c_{{\Gamma }}) = \{\langle {w_{0},c_{{\Gamma }^{\alpha }}}\rangle \}$. Hence, $\mathcal {E},w_{0},c_{{\Gamma }} \Vdash$ iff $\mathcal {E},w_{0},c_{{\Gamma }^{\alpha }} \Vdash \beta$. But again by induction hypothesis, this holds iff β ∈Γ^α, i.e., . □

We are now ready to prove (ii). iff $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w,c) \subseteq \llbracket {\beta }\rrbracket ^{\mathcal {E}}$. By Claim 1, $\langle w_{\gamma },c_{{\Phi }_{w}} \rangle \in \llbracket {\alpha }\rrbracket ^{\mathcal {E}}$ iff γ = α. Hence, $f(\llbracket {\alpha }\rrbracket ^{\mathcal {E}},w,c) = \{\langle {w_{0},c_{{\Phi }_{w}^{\alpha }}}\rangle \}$. So iff $\mathcal {E},w_{0},c_{{\Phi }_{w}^{\alpha }} \Vdash \beta$, which by Claim 2 holds iff $\beta \in {\Phi }_{w}^{\alpha }$, i.e., . □

Corollary 3

Let 𝜃 be any consistent S5-formula, and let 𝜃^∗ be the result of uniformly substituting one or more atomic sentences in 𝜃 for distinct counterfactuals. Then 𝜃^∗ is $\exp$-satisfiable.

Now we can establish Theorem 1(b):

Proof Proof (Theorem 1(b))

Let $\mathcal {I} = \langle W,P,f,V \rangle$ and first let w ∈ P. Let:

$$ \begin{array}{@{}rcl@{}} {\Phi} & {=}& \{\phi ~|~ \phi \text{ is an $\textbf{S5}$-formula and } \mathcal{I},w \Vdash_\textsf{i} \phi] \\ {\Psi} & {=}& \{\phi~|~\phi \text{ is a counterfactual and } \mathcal{I},w \Vdash_\textsf{i} \phi]. \end{array} $$

By Proposition 2, there is a expressivist model $\mathcal {I}^{\exp } = \langle W,f^{\exp } \rangle$ and a classical hyperconvention c such that $\mathcal {I}^{\exp },w,c \Vdash _{\exp } {\Phi } \cup {\Psi }$ and if ϕ is a counterfactual not in Ψ, $\mathcal {I}^{\exp },w,c \nVdash _{\exp } \phi$. Hence, by a simple induction, $\mathcal {I},w \Vdash _{\textsf {i}} \phi$ iff $\mathcal {I}^{\exp },w,c \Vdash _{\exp } \phi$.

Now let w∉P. Let Γ = {ϕ | V (ϕ,w) = 1} and let $\mathcal {I}^{\exp }$ be 〈W,f〉 where f is constructed as in Proposition 2. Then by Claim 2, $\mathcal {I}^{\exp },w_{0},c_{{\Gamma }} \Vdash _{\exp } \phi$ iff ϕ ∈Γ. Hence, we can take x = 〈w₀,c_Γ〉. □