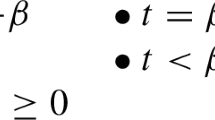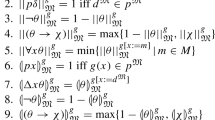Abstract
Robert Stalnaker recently proposed a simple theory of propositions using the notion of a set of propositions being consistent, and conjectured that this theory is equivalent to the claim that propositions form a complete atomic Boolean algebra. This paper clarifies and confirms this conjecture. Stalnaker also noted that some of the principles of his theory may be given up, depending on the intended notion of proposition. This paper therefore also investigates weakened constraints on consistency and the corresponding classes of Boolean algebras.
Similar content being viewed by others
References
Birkhoff, G. (1940). Lattice theory. New York: American Mathematical Society.
Davey, B.A., & Priestley, H.A. (2002). Introduction to lattices and order, 2nd edn. Cambridge: Cambridge University Press.
Fox, C., & Lappin, S. (2005). Foundations of intensional semantics. Malden: Blackwell Publishing.
Givant, S., & Halmos, P. (2009). Introduction to Boolean algebras. New York: Springer.
Jech, T. (2002). Set theory, 3rd edn. Berlin: Springer.
Pollard, C. (2008). Hyperintensions. Journal of Logic and Computation, 18, 257–282.
Saliı̆, V.N. (1988). Lattices with unique complements. Providence: American Mathematical Society.
Stalnaker, R. (1976). Possible worlds. Noûs, 10, 65–75.
Stalnaker, R. (1984). Possible worlds. In Inquiry, chapter 3 (pp. 43–58). Cambridge: MIT Press.
Stalnaker, R. (2003). Possible worlds. In Ways a world might be, chapter 1 (pp. 25–39). Oxford: Clarendon Press.
Stalnaker, R. (2012). Mere possibilities. Princeton: Princeton University Press.
Stalnaker, R. (2018). A Quinean foundation for modal logic. Handouts for The Rutgers Lectures in Philosophy 2018. A book based on these lectures is to be published by Oxford University Press.
Acknowledgements
I would like to thank Robert Stalnaker for email correspondence out of which this paper developed. The proofs of Lemmas 5 and 24 are due to Stalnaker (p.c.), as is the suggestion to consider the principle of upward closure; I am grateful for being able to include them here. Thanks also to a reviewer for this journal, as well as to Andrew Bacon, Michael Caie, Cian Dorr and Jeremy Goodman for very helpful discussion.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Fritz, P. On Stalnaker’s Simple Theory of Propositions. J Philos Logic 50, 1–31 (2021). https://doi.org/10.1007/s10992-020-09557-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-020-09557-6