Nested exposure case-control sampling: a sampling scheme to analyze rare time-dependent exposures

Abstract

For large cohort studies with rare outcomes, the nested case-control design only requires data collection of small subsets of the individuals at risk. These are typically randomly sampled at the observed event times and a weighted, stratified analysis takes over the role of the full cohort analysis. Motivated by observational studies on the impact of hospital-acquired infection on hospital stay outcome, we are interested in situations, where not necessarily the outcome is rare, but time-dependent exposure such as the occurrence of an adverse event or disease progression is. Using the counting process formulation of general nested case-control designs, we propose three sampling schemes where not all commonly observed outcomes need to be included in the analysis. Rather, inclusion probabilities may be time-dependent and may even depend on the past sampling and exposure history. A bootstrap analysis of a full cohort data set from hospital epidemiology allows us to investigate the practical utility of the proposed sampling schemes in comparison to a full cohort analysis and a too simple application of the nested case-control design, if the outcome is not rare.

Appendices

A Theoretical background

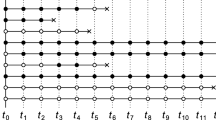
The following presentation is based on Borgan et al. (1995).

Fix $[0, \tau ]$, $\tau \in (0,\infty ]$ and consider a cohort $\mathscr {C}=\{1,\ldots ,n\}$ and a probability space $(\varOmega , \mathscr {F}, \mathbb {P})$. On this space, the marked point process $\{(t_j, i_j), j\ge 1\}$, consists of the failure times $t_j\in [0,\tau ]$ and the mark $i_j\in \mathscr {C}$, that typifies the outcome positive individual at this point in time. The information at time-origin and generated by this process over time is included in the filtration $(\mathscr {F}_{t})_{t\ge 0}$. We assume the counting process of the observed failure times to be

$$\begin{aligned} N_i(t)=\sum _{j\ge 1}\mathbb {1} \left\{ t_j\le t,\, i_j=i \right\} , \qquad i\in \mathscr {C}, \end{aligned}$$

and its intensity is $\lambda _i(t)=Y_i(t)\alpha _0(t)\exp ({\varvec{\beta }}^T\mathbf {z}_i(t))$. The at-risk indicator $Y_i$ and the covariates $\mathbf {z}_i(t)$ are assumed to be left-continuous and adapted to $(\mathscr {F}_{t})_{t\ge 0}$. Let ${\widetilde{\mathscr {R}}}_j$ denote the sampled risk set consisting of the controls together with the matched outcome positive individual $i_j$. The resulting marked point process is $\{(t_j, (i_j, {\widetilde{\mathscr {R}}}_j)), j\ge 1\}$ with the finite mark space $E=\{(i,{R}){:}\,{R} \in \mathscr {P}, i \in {R} \}=\{(i,{R}){:}\,{R} \subset \mathscr {C}, {R} \in \mathscr {P}_i \}$, where $\mathscr {P}$ is the powerset of $\mathscr {C}$. Using this construction, we extend $(\mathscr {F}_{t})_{t\ge 0}$ to $(\mathscr {H}_{t})_{t\ge 0}=(\mathscr {F}_{t}\vee \sigma ({\widetilde{\mathscr {R}}}_j; t_j\le t))_{t\ge 0}$ by the sampling process. For each tuple $(i,{R})\in E$, there exists a corresponding counting process

$$\begin{aligned} N_{(i,{R})}(t)=\sum _{j\ge 1}\mathbb {1} \left\{ t_j\le t,\, i_j=i,\; {\widetilde{\mathscr {R}}}_j={R} \right\} \end{aligned}$$

(7)

that counts all observed failure times of individual i in [0, t] within the sampled risk set ${R}$. We assume that the sampling procedure is independent in the sense that the $\mathscr {F}_{t}-$intensity processes of $N_{i}(t):=\sum _{{R} \in \mathscr {P}_i}N_{(i,R)}(t)$ and their counterparts w.r.t $\mathscr {H}_{t}$ coincide (Andersen et al. 1993, Sec. III.2). Using $\pi \left( {R} |t,i\right) :=\mathbb {P}\left( {R} \text { sampled at } t|dN_i(t)=1, \mathscr {H}_{t-}\right)$ with $\pi \left( {R} |t,i\right) =0$ if $Y_i(t)=0$ and $\pi \left( {R} |t,i\right) =0$ if $i\notin {R}$ we obtain

$$\begin{aligned} \lambda _{(i,R)}(t)=\lambda _i(t)\pi \left( {R} |t,i\right) =Y_i(t)w_i(t,{R})\pi \left( {R} |t\right) \alpha \left( t|\mathbf {z}_i(t)\right) \end{aligned}$$

(8)

as the intensity process for the counting process (7), where $\pi \left( {R} |t\right) =n_\bullet ^{-1}(t)\sum _{i=1}^{n}\pi \left( {R} |t,i\right)$ and $w_i(t,{R})={\pi \left( {R} |t,i\right) }/{\pi \left( {R} |t\right) }$ characterizes the weight. The inference is based on the partial likelihood given by

$$\begin{aligned} \mathscr {L}({\varvec{\beta }})=\prod _{t_i}\frac{\exp ({\varvec{\beta }}^T\mathbf {z}_i(t_i))\cdot w_i(t_i,{\widetilde{\mathscr {R}}}_i)}{\sum _{\ell \in {\widetilde{\mathscr {R}}}_i}\exp ({\varvec{\beta }}^T\mathbf {z}_\ell (t_i))\cdot w_\ell (t_i,{\widetilde{\mathscr {R}}}_i)}. \end{aligned}$$

(9)

In conclusion, only outcome positive individuals with their respective time of failure $t_i$ as well as the corresponding sampled risk sets ${\widetilde{\mathscr {R}}}_i$ contribute to the inference based on this model. The estimator ${\widehat{{\varvec{\beta }}}}$ is obtained by maximizing the partial likelihood (9). Theoretical properties and asymptotic results can be obtained from Borgan et al. (1995).

The question of how to specify $\pi \left( \cdot |t,i\right)$ for every t where $Y_i(t)=1$ arouses immediately. The probability can be based on information available until but not including time t, i.e. $\pi \left( {R} |t, i\right)$ is left-continuous and adapted. Using this, we develop the new sampling procedure for investigating the association between a time-dependent exposure and the outcome by simultaneously sampling with respect to this exposure.

For the NECC, we consider a random variable $B{:}\,\left( \varOmega ,[0,\tau ]\right) \rightarrow \{0,1\}$ indicating whether an individual should be considered as a case within the partial likelihood, i.e. whether controls should be assigned to that observed outcome event. Further, we write $B(t):=B(\omega , t)$, $\mathscr {R}_\bullet (t)=\{i{:}\,Y_i(t\text {-})=1\}$ and $\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R}):=\mathbb {P}({\widetilde{\mathscr {R}}}(t)={R} |dN_i(t)=1, \mathscr {H}_{t\text {-}})$. We consider the failure time $t_j$ and assume that for the respective individual the sampled risk set only contains $i_j$, i.e. no controls are sampled. Thus, the contribution to the likelihood is then given by

$$\begin{aligned} \frac{\exp ({\varvec{\beta }}^T\mathbf {z}_j(t_j))\cdot \pi \left( {\widetilde{\mathscr {R}}}_j |t_j,i_j\right) }{\sum _{\ell \in {\widetilde{\mathscr {R}}}_j}\exp ({\varvec{\beta }}^T\mathbf {z}_\ell (t_j))\cdot \pi \left( {\widetilde{\mathscr {R}}}_j |t_j,\ell \right) }=\frac{\exp ({\varvec{\beta }}^T\mathbf {z}_j(t_j))\cdot \pi \left( {\widetilde{\mathscr {R}}}_j |t_j,i_j\right) }{\exp ({\varvec{\beta }}^T\mathbf {z}_j(t_j))\cdot \pi \left( {\widetilde{\mathscr {R}}}_j |t_j,i_j\right) }=1. \end{aligned}$$

Formalizing the NECC sampling design which was discussed in Sect. 2 we obtain as the sampled risk sets

$$\begin{aligned} {\widetilde{\mathscr {R}}}_j={\left\{ \begin{array}{ll} \{i_j, k_1,\ldots ,k_{m-1}\}, k_\ell \in \mathscr {R}_{\bullet }(t_j) &{}\quad \text {if}\,\,x_{j}(t_j)=1\\ \{i_j, k_1,\ldots ,k_{m-1}\}, k_\ell \in \mathscr {R}_{\bullet }(t_j) &{}\quad \text {if}\,\,x_{j}(t_j)=0 \text { and } B(t_j)=1\\ \{i_j\} &{}\quad \text {if}\,\,x_{j}(t_j)=0 \text { and } B(t_j)=0. \end{array}\right. } \end{aligned}$$

Using ${\widetilde{\mathscr {R}}}_j$ and defining $\mathscr {R}_0(t)=\{i:Y_i(t\text {-})=1, x_i(t)=0\}$ and $n_\bullet (t)={\text {card}}\left( \mathscr {R}_\bullet (t)\right)$, we derive

$$\begin{aligned} \pi \left( {R} |t,i\right)&=\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R})\nonumber \\&=\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R}, x_i(t\text {-})=1)+ \mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R}, x_i(t\text {-})=0, B(t)=1) \nonumber \\&\quad +\,\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R}, x_i(t\text {-})=0, B(t)=0)\nonumber \\&=\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R} |x_i(t\text {-})=1)\mathbb {P}_{t\text {-}}(x_i(t\text {-})=1)\nonumber \\&\quad +\,\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R} |x_i(t\text {-})=0, B(t)=1)\mathbb {P}_{t\text {-}}(x_i(t\text {-})=0)\mathbb {P}_{t\text {-}}(B(t)=1| x_i(t\text {-})=0)\nonumber \\&\quad +\,\mathbb {P}_{t\text {-}}({\widetilde{\mathscr {R}}}(t)={R} |x_i(t\text {-})=0, B(t)=0)\mathbb {P}_{t\text {-}}(x_i(t\text {-})=0)\mathbb {P}_{t\text {-}}(B(t)=0| x_i(t\text {-})=0)\nonumber \\&=\left( {\begin{array}{c}n_\bullet (t)-1\\ m-1\end{array}}\right) ^{-1}\mathbb {1}_{\left( i\in {R}, {\text {card}}\left( {R} \right) =m, {R} \subset \mathscr {R}_\bullet (t)\right) }\mathbb {1} \left\{ x_i(t\text {-})=1 \right\} \nonumber \\&\quad +\,\left( {\begin{array}{c}n_\bullet (t)-1\\ m-1\end{array}}\right) ^{-1}\mathbb {1}_{\left( i\in {R}, {\text {card}}\left( {R} \right) =m, {R} \subset \mathscr {R}_\bullet (t)\right) }\mathbb {1} \left\{ x_i(t\text {-})=0 \right\} \mathbb {P}_{t\text {-}}(B(t)=1|x_i(t\text {-})=0) \nonumber \\&\quad +\,\mathbb {1}_{\left( \{i\}={R}, {R} \subset \mathscr {R}_0(t)\right) }\mathbb {1} \left\{ x_i(t\text {-})=0 \right\} \mathbb {P}_{t\text {-}}(B(t)=0|x_i(t\text {-})=0), \end{aligned}$$

(10)

where $\mathbb {P}_{t\text {-}}(x_i(t\text {-})=a)=\mathbb {1} \left\{ x_i(t\text {-})=a \right\}$ for $a\in \{0,1\}$. Equation (10) can be used for the calculation of the denominator of the weight. The structure of the random variable B allows for several sampling procedures within the NCC.

We choose $B(t)\sim \text {Ber}(q(t))$, i.e. independently Bernoulli distributed with probability $q(t)\in (0,1]$. In the simplest setting, $q(t)$ is deterministic from the very beginning. The sampling probabilities and weights can be calculated with $m_0(t)={\text {card}}\left( \mathscr {R}_0(t)\cap {\widetilde{\mathscr {R}}}(t)\right)$ by

$$\begin{aligned} \pi \left( {R} |t,i\right)&=\left( {\begin{array}{c}n_\bullet (t)-1\\ m-1\end{array}}\right) ^{-1}\mathbb {1}_{\left( i\in {R}, {\text {card}}\left( {R} \right) =m, {R} \subset \mathscr {R}_\bullet (t)\right) }\left( \mathbb {1} \left\{ x_i(t\text {-})=1 \right\} +\mathbb {1} \left\{ x_i(t\text {-})=0 \right\} q(t)\right) \\&\quad +\,\mathbb {1} \left\{ \{i\}={R}, {R} \subset \mathscr {R}_0(t) \right\} \mathbb {1} \left\{ x_i(t\text {-})=0 \right\} (1-q(t))\\ \pi \left( {R} |t\right)&=\frac{1}{n_\bullet (t)}\sum _{i=1}^{n}\pi \left( {R} |t,i\right) \\&\quad = \frac{1}{n_\bullet (t)}\left( {\begin{array}{c}n_\bullet (t)-1\\ m-1\end{array}}\right) ^{-1}\mathbb {1}_{\left( {\text {card}}\left( {R} \right) =m, {R} \subset \mathscr {R}_\bullet (t)\right) }\left[ m-m_0(t)+ q(t)m_0(t)\right] \nonumber \\&\quad +\,\mathbb {1} \left\{ {\text {card}}\left( {R} \right) =1, {R} \subset \mathscr {R}_{0} \right\} (1-q(t))\\ w_i(t,{R})&=\frac{q(t)^{1-x_i(t)}n_\bullet (t)}{m-m_0(t)+q(t)\cdot m_0(t)}\mathbb {1} \left\{ i\in {R}, {\text {card}}\left( {R} \right) =m, {R} \subset {\widetilde{\mathscr {R}}}_\bullet (t) \right\} . \end{aligned}$$

In Sect. 2.4 we set $q=1$ to state the history-dependent sampling scheme. This contradicts the requirement above, since $q(t)=0$ if the inequality in (6b) is fulfilled. A motivation for excluding zero from the interval of the inclusion probability is as follows: Let $q(t)=0$ for some t. Then weights take the form

meaning whenever a risk set has the same exposure value, the weight in (11a) will be infinite. If there are different exposure levels in a risk set, the set will be uninformative [the ratio in Eq. (9) is one] or destructive for the partial likelihood since the ratio equals zero [see Eq. (11b)]. Either way, in all cases the estimation of the log hazard ratio by the partial likelihood will be disrupted.

Sampling non-exposed individuals as cases is mandatory for the NECC to meaningful estimate the log hazard rate ${\varvec{\beta }}$ within the Cox proportional hazards model. Assume we only consider exposed individuals as cases, then for every nominator in Equation (9) we obtain

$$\begin{aligned} \exp ({\varvec{\beta }}^T \mathbf {z}_i(t_i))= & {} \exp \left( [\beta _{1}, \beta _{2},\ldots , \beta _{p}] \times [x_i(t_i)=1, z_{i1}(t_i), z_{ip-1}(t_i)]^T \right) \\= & {} \exp (\beta _1)\times \exp \left( [\beta _{2},\ldots , \beta _{p}] \times [z_{i1}(t_i), z_{ip-1}(t_i)]^T\right) , \end{aligned}$$

where $\mathbf {y}=[y_1, \ldots , y_n]^T \in \mathbb {R}^n$. For the ease of presentation, we consider the projection on the first component of ${\varvec{\beta }}$, i.e. the estimation of the regression parameter $\beta _1$ associated to the main exposure. We stratify the sampled risk set into ${\widetilde{\mathscr {R}}}_i={\widetilde{\mathscr {R}}}_i^0{\dot{\cup }} {\widetilde{\mathscr {R}}}_i^1$ using the covariate values $x(t_i)$. The $w_i(t_i, {R})$ only depend on the exposure status within one fixed risk set

$$\begin{aligned} \mathscr {L}_i(\beta _1)&=\frac{\exp (\beta _1x_i(t_i))w_i(t_i,{R})}{\sum _{\ell \in {\widetilde{\mathscr {R}}}_i}\exp (\beta _1x_\ell (t_i))w_\ell (t_i,{R})}\\&=\frac{w_i(t_i,{R})}{e^{-\beta _1}\sum _{\ell \in {\widetilde{\mathscr {R}}}_i}\exp (\beta _1x_\ell (t_i))w_\ell (t_i,{R})}\\&=\frac{w_i(t_i,{R})}{e^{-\beta _1}(\sum _{\ell \in {\widetilde{\mathscr {R}}}_i^0}\exp (\beta _1(x_\ell (t_i)=0))w_\ell (t_i,{R}) + \sum _{\ell \in {\widetilde{\mathscr {R}}}_i^1}\exp (\beta _1(x_\ell (t_i)=1))w_\ell (t_i,{R}))}\\&=\frac{1}{e^{-\beta _1}{\text {card}}\left( {\widetilde{\mathscr {R}}}_i^0\right) q(t_i) + {\text {card}}\left( {\widetilde{\mathscr {R}}}_i^1\right) }, \end{aligned}$$

which is maximized by $\beta _1=\infty$. This leads to $\max _{\beta _1} \mathscr {L}(\beta _1) =\infty$ and thus, an inappropriate estimation if we only consider exposed individuals ($x_i(t_i)=1$) to become cases.

B Results traditional nested case-control design

Table 5 follows the structure of Table 1 in the main document and gives the results for a bootstrap analysis of the SIR 3 data using the traditional NCC.

Table 5 Results from 10,000 bootstrap simulations of the full cohort and an NCC design with one up to four controls