Skip to main content
SpringerLink
Log in

Scaling relations between riparian vegetation and stream order in the Whitewater River network, Kansas, USA

  • Research Article
  • Published:
Landscape Ecology Aims and scope Submit manuscript

Abstract

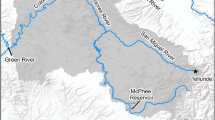
Riparian communities have been well-studied along individual streams, but not within the context of networks of which streams are a part. To study networks, hydrologists use Horton–Strahler ordering to assign streams to discrete categories in which increasing numerical value (ω) reflects increasing size of the stream and complexity of the network. A key use of this classification method has been to demonstrate scaling relations between hydrogeomorphic variables and order. These relations now provide a foundation to determine how ecological processes are associated with the geometry and topology of river networks. We used geographic information systems (GIS) to map and measure the stream network and riparian vegetation of the Whitewater River basin of eastern Kansas, USA. With the resulting data, we tested if (1) riparian vegetation scaled with order, and (2) riparian vegetation at confluences of two streams differed from that found along constituent streams. Most characteristics of riparian vegetation scaled with order. In confluence zones, density and diversity of riparian vegetation generally were equivalent to that of the largest constituent stream. Scaling relations between riparian vegetation and order provide a framework to quantify the role of riparian vegetation in the water balance of stream networks and a tool to predict area and distribution of riparian vegetation from network topology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Aber JS (1991) Surficial geology of Butrler County, Kansas. Kansas Geological Survey Open File Report 1991-48

  • Abrams MD, Knapp AK (1986) Seasonal water relations of three gallery forest hardwood species in northeast Kansas. For Sci 32:687–696

    Google Scholar 

  • Brown JH, Gupta VK, Li B, Milne BT, Restrepo C, West GB (2002) The fractal nature of nature: power laws, ecological complexity and biodiversity. Philos Trans R Soc Lond B 357:619–626. doi:10.1098/rstb.2001.0993

    Article  Google Scholar 

  • Brown JH, Gillooly JF, Allen AP, Savage VM, West GB (2004) Toward a metabolic theory of ecology. Ecology 85:1771–1789

    Article  Google Scholar 

  • Clayton JA, Kean JW (2010) Establishing a multi-scale stream gaging network in the Whitewater River basin, Kansas, USA. Water Resour Manag. doi:10.1007/ws11269-010-9624-x

  • Dill KA, Bromberg S (2002) Molecular driving forces: statistical thermodynamics in chemistry and biology. Oxford University Press, London

    Google Scholar 

  • Eckness P, Randhir T (2007) Effects of riparian areas, stream order, and land use disturbance on watershed-scale habitat potential: an ecohydrologic approach to policy. J Am Water Resour Assoc 43:1468–1482

    Google Scholar 

  • Egbert SL, Peterson DL, Stewart AM, Lauver CL, Blodgett CF, Price KP, Martinko EA (2001) The Kansas gap land cover map: final report. Kansas Biological Survey Report #98. Lawrence

  • Enquist BJ, Economo EP, Huxman TE, Allen AP, Ignace DD, Gillooly JF (2003) Scaling metabolism from organisms to ecosystems. Nature 423:639–642

    Google Scholar 

  • Enquist BJ, West GB, Brown JH (2009) Extensions and evaluations of a general quantitative theory of forest structure and dynamics. Proc Natl Acad Sci USA. www.pnas.org/cgi/doi/10.1073/pnas.0812303106

  • Fern A, Musavi MT, Miranda J (1998) Automatic extraction of drainage network from digital terrain intercept data: a local network approach. IEEE Trans Geosci Remote Sens 36:1007–1011

    Article  Google Scholar 

  • Fisher SG (1997) Creativity, idea generation, and the functional morphology of streams. J N Am Benthol Soc 16:305–318

    Article  Google Scholar 

  • Forman RTT, Godron M (1986) Landscape ecology. Wiley, New York

    Google Scholar 

  • Gregory SV, Swanson FJ, McKee WA, Cummins KW (1991) An ecosystem perspective of riparian zones: focus on links between land and water. Bioscience 41:540–551

    Article  Google Scholar 

  • Gupta VK, Mantilla R, Troutman BM, Dowdy D, Krajewski WF (2010) Generalizing a nonlinear geophysical flood theory to medium-sized river networks. Geophys Res Lett 37:L11402. doi:10.1029/2009GL041540,2010

    Article  Google Scholar 

  • Harris LD (1984) The fragmented forest: island biogeography theory and the preservation of biotic diversity. University of Chicago Press, Chicago

    Google Scholar 

  • Harte J, Zillio T, Conlisk F, Smith AB (2008) Maximum entropy and the state-variable approach to macroecology. Ecology 89:2700–2711

    Article  PubMed  CAS  Google Scholar 

  • Horton RE (1945) Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology. Geol Soc Am Bull 56:275–370

    Article  Google Scholar 

  • Johnson WC (1994) Woodland expansions in the Platte River, Nebraska: patterns and causes. Ecol Monogr 64:45–84

    Article  Google Scholar 

  • Knopf FL (1986) Changing landscapes and the cosmopolitism of the eastern Colorado avifauna. Wildl Soc Bull 14:132–142

    Google Scholar 

  • Leopold B, Miller JP (1956) Ephemeral streams-hydraulic factors and their relation to the drainage net. U. S. Geological Survey Professional Papers, 282-A, pp 1–37

  • MacArthur RH (1972) Geographical ecology: patterns in the distribution of species. Princeton University Press, Princeton

    Google Scholar 

  • Malard F, Tockner K, Dole-Olivier M, Ward JV (2002) A landscape perspective of surface–subsurface exchanges in river corridors. Freshw Biol 47:621–640

    Article  Google Scholar 

  • Mantilla R, Gupta VK (2005) A GIS numerical framework to study the process basis of scaling statistics in river networks. IEEE Geosci Remote Sens Lett 2:404–408

    Article  Google Scholar 

  • Mantilla R (2007) Physical basis of statistical scaling in peak flows and stream flow hydrographs for topologic and spatially embedded random self-similar channel networks. Dissertation, University of Colorado

  • Mantilla R, Troutman BM, Gupta VK (2010) Testing statistical self-similarity in the topology of river networks. J Geophy Res 115, F03038. doi:10.1029/2009Jf001609

  • Martin CW, Johnson WC (1987) Historical channel narrowing and riparian vegetation expansion in the Medicine Lodge River Basin, Kansas, 1871–1983. Ann Assoc Am Geogr 77:436–449

    Article  Google Scholar 

  • McConnell M, Gupta VK (2008) A proof of the Horton law of stream numbers for the Tokunaga model of river networks. Fractals 16:227–233

    Article  Google Scholar 

  • Melton MA (1959) A derivation of Strahler’s channel-ordering system. J Geol 67:345–346

    Article  Google Scholar 

  • National Research Council (2002) Riparian areas: functions and strategies for management. National Academy Press, Washington, DC

    Google Scholar 

  • Ni B, Pallardy SG (1990) Response of liquid flow resistance to soil drying in seedlings of four deciduous angiosperms. Oecologia 84:260–264

    Google Scholar 

  • O’Callaghan J, Mark D (1984) The extraction of drainage networks from digital intercept data. Comput Vis Graph Image Process 28:323–344

    Article  Google Scholar 

  • Peckham SD, Gupta VK (1999) A reformulation of Horton’s laws for large river networks in terms of statistical self-similarity. Water Resour Res 35:2763–2777

    Article  Google Scholar 

  • Penner HL, Eckart SC, Ewing DA, Schmidt G, Smith J (1975) Soil survey of Butler County. United States Department of Agriculture, Natural Resource Conservation Service, Kansas

    Google Scholar 

  • Poff NL, Allan JD, Bain MB, Karr JR, Prestegaard KL, Richter B, Sparks R, Stromberg J (1997) The natural flow regime: a new paradigm for riverine conservation and restoration. Bioscience 47:769–784

    Article  Google Scholar 

  • Poole GC (2002) Fluvial landscape ecology: addressing uniqueness within the river discontinuum. Freshw Biol 47:641–660

    Article  Google Scholar 

  • Preston FW (1962) The canonical distribution of commonness and rarity, part I. Ecology 43:186–216

    Google Scholar 

  • Rinaldo A, Banavar JR, Maritan A (2006) Trees, networks, and hydrology. Water Resour Res 42:W06D07. doi:10.1029/2005WR004108

  • Ritchie ME, Olff H (1999) Spatial scaling laws yield a synthetic theory of biodiversity. Nature 400:557–560

    Article  PubMed  CAS  Google Scholar 

  • Rodriguez-Iturbe I, Rinaldo A (1997) Fractal river basins. Cambridge University Press, New York

    Google Scholar 

  • Schumm SA (1963) Sinuosity of alluvial rivers on the Great Plains. Geol Soc Am Bull 74:1089–1100

    Article  Google Scholar 

  • Shmida A, Wilson MV (1985) Biological determinants of species diversity. J Biogeogr 12:1–20

    Article  Google Scholar 

  • Smith CE (1998) Modeling high sinuosity meanders in a small flume. Geomorphology 25:19–30

    Article  Google Scholar 

  • Strahler AN (1952) Hypsometric (area altitude) analysis of erosional topography. Geol Soc Am Bull 63:1117–1142

    Article  Google Scholar 

  • Tabacchi E, Correll DL, Hauer R, Pinay G, Planty-Tabacchi A, Wissmar RC (1998) Development, maintenance and role of riparian vegetation in the river landscape. Freshw Biol 40:497–516

    Article  Google Scholar 

  • Tokunaga E (2003) Tiling properties of drainage basins and their physical bases. In: Evans IS, Dikau R, Tokunaga E, Ohmoria H, Hirano M (eds) Concepts and modeling in geomorphology: international perspectives. Terrapub, Tokyo, pp 147–166

    Google Scholar 

  • Troutman BM (2005) Scaling of flow distance in random self-similar channel networks. Fractals 13(4):265–282

    Article  Google Scholar 

  • Turner MG, Gergel SE, Dixon MD, Miller JR (2004) Distribution and abundance of trees in floodplain forests of the Wisconsin River: environmental influences at different scales. J Veg Sci 15:729–738

    Google Scholar 

  • van Coller AL, Rogers KH, Heritage GL (2000) Riparian vegetation–environment relationships: complimentarity of gradients versus patch hierarchy approaches. J Veg Sci 11:337–350

    Article  Google Scholar 

  • VanLooy JA, Martin CW (2005) Channel and vegetation change on the Cimarron River, southwestern Kansas, 1953–2001. Ann Assoc Am Geogr 95:727–739

    Article  Google Scholar 

  • Vannote RL, Minshall GW, Cummins KW, Sedell JR, Cushing CE (1980) The river continuum concept. Can J Fish Aquat Sci 37:130–137

    Article  Google Scholar 

  • Ward JV, Stanford JA (1995) Ecological connectivity in alluvial river ecosystems and its disruption by flow regulation. Regul Rivers Res Manag 11:105–119

    Article  Google Scholar 

  • West GB, Brown JH, Enquist BJ (1997) A general model for the origin of allometric scaling laws in biology. Science 276:122–126

    Article  PubMed  CAS  Google Scholar 

  • Whittaker RH (1975) Communities and ecosystems. MacMillan, New York

    Google Scholar 

  • Wooster DE, DeBano SJ (2006) Effect of woody riparian patches in croplands on stream macroinvertebrates. Arch Hydrobiol 165:241–268

    Article  Google Scholar 

  • Zar JH (1974) Biostatistical analysis, 4th edn. Prentice-Hall, Englewood Cliffs

    Google Scholar 

Download references

Acknowledgments

T. and P. Neville, New Mexico Natural Heritage Program, and K. Menke, BirdsEyeView GIS, Inc. assisted with GIS analyses. H. Delaney, University of New Mexico, assisted with statistical analysis. J. H. Brown, University of New Mexico, and two anonymous reviewers provided helpful comments of earlier drafts. This study was partially funded by NSF Grant No. 04-50385 to the University of New Mexico, and NSF Grant No. EAR 1005311 to the University of Colorado.

Author information

Authors and Affiliations

  1. Department of Biology, 1 MSC 03 2020, University of New Mexico, Albuquerque, NM, 87131, USA

    William C. Dunn & Bruce T. Milne

  2. IIHR—Hydroscience & Engineering, The University of Iowa, Iowa City, IA, 52242, USA

    Ricardo Mantilla

  3. Department of Civil, Environmental and Architectural Engineering, Cooperative Institute for Research in Environmental Sciences, University of Colorado, Boulder, CO, 80309, USA

    Vijay K. Gupta

Authors
  1. William C. Dunn
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bruce T. Milne
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ricardo Mantilla
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Vijay K. Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to William C. Dunn.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dunn, W.C., Milne, B.T., Mantilla, R. et al. Scaling relations between riparian vegetation and stream order in the Whitewater River network, Kansas, USA. Landscape Ecol 26, 983–997 (2011). https://doi.org/10.1007/s10980-011-9622-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10980-011-9622-2

Keywords

Search

Navigation