Skip to main content
SpringerLink
Log in

On model for Darcy–Forchheimer 3D nanofluid flow subject to heat flux boundary condition

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

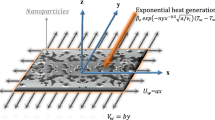
This paper provides a theoretical study of 3D nanofluid flow with zero nanoparticles mass and constant heat fluxes conditions. An incompressible Newtonian nanoliquid saturates the permeable media describing the Darcy–Forchheimer (DF) relation. A bidirectional stretchable sheet has been considered to produce the three-dimensional flow. Appropriate variables are considered to change the PDEs into the ODEs. The obtained nonlinear framework is computed by the optimal homotopic technique. Outcomes of numerous emerging flow factors on concentration and the temperature of nanoparticles are explored. Heat transport rate and skin frictions have been tabulated and analyzed. The presented data reveal that temperature distribution is upgraded for larger estimations of Forchheimer number. Furthermore, the heat transport rate reduces when thermophoresis number enhances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Abbreviations

\(u, v, w\) :

Velocity components (m s−1)

\(C_{\infty }\) :

Ambient fluid concentration

\(k\) :

Thermal conductivity (W m−1 K−1)

\(\nu\) :

Kinematic viscosity (m2 s−1)

\(T\) :

Temperature (K)

\(C_{\text{b}}\) :

Drag coefficient

\(\mu\) :

Dynamic viscosity (Pa s)

\(a, b\) :

Stretching constants (s−1)

\(K^{*}\) :

Permeability of porous medium

\(\left( {\rho c} \right)_{\text{f}}\) :

Heat capacity of liquid (J Kg−3 K−1)

\(f^{\prime}, g'\) :

Dimensionless velocities

\(\phi\) :

Dimensionless concentration

\({\text{Nu}}_{\text{x}}\) :

Local Nusselt number

\(N_{\text{t}}\) :

Thermophoresis number

\(N_{\text{b}}\) :

Brownian movement number

\(\lambda\) :

Porosity parameter

\(\alpha\) :

Ratio parameter

\({\text{Re}}_{\text{x}} ,\;{\text{Re}}_{\text{y}}\) :

Local Reynolds numbers

\(x, y, z\) :

Coordinate axes (m)

\(\alpha_{\text{m}}\) :

Thermal diffusivity (m2 s−1)

\(\rho_{\text{f}}\) :

Base fluid density (kg m−3)

\(F\) :

Non-uniform inertia coefficient

C :

Concentration

\(D_{\text{B}}\) :

Brownian diffusion coefficient (m2 s−1)

\(q_{\text{w}}\) :

Wall heat flux (W m−2)

\(D_{\text{T}}\) :

Thermophoretic diffusion coefficient (m2 s−1)

\(T_{\infty }\) :

Ambient fluid temperature (K)

\(\left( {\rho c} \right)_{\text{p}}\) :

Nanoparticles effective heat capacity (J kg−3K−1)

\(\zeta\) :

Dimensionless variable

\(\theta\) :

Dimensionless temperature

\({\text{Sc}}\) :

Schmidt number

\({\text{Sh}}_{\text{x}}\) :

Local Sherwood number

\({ \Pr }\) :

Prandtl number

\(C_{\text{fx}} , C_{\text{fy}}\) :

Skin friction coefficients

\(F_{\text{r}}\) :

Forchheimer parameter

\(N_{j}^{*}\) :

Arbitrary constants

References

  1. Cai J, Hu X, Xiao B, Zhou Y, Wei W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int J Heat Mass Transf. 2017;105:623–37.

    CAS  Google Scholar 

  2. Ahn HS, Kim MH. A review on critical heat flux enhancement with nanofluids and surface modification. J Heat Transf. 2012;134:024001.

    Google Scholar 

  3. Buongiorno J. Convective transport in nanofluids. J Heat Transf. 2006;128:240–50.

    Google Scholar 

  4. Makinde OD, Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Therm Sci. 2011;50:1326–32.

    CAS  Google Scholar 

  5. Bachok N, Ishak A, Pop I. Flow and heat transfer over a rotating porous disk in a nanofluid. Phys B Condens Matter. 2011;406:1767–72.

    CAS  Google Scholar 

  6. Hsiao KL. Nanofluid flow with multimedia physical features for conjugate mixed convection and radiation. Comp Fluids. 2014;104:1–8.

    Google Scholar 

  7. Kuznetsov AV, Nield DA. Natural convective boundary-layer flow of a nanofluid past a vertical plate: a revised model. Int J Therm Sci. 2014;77:126–9.

    Google Scholar 

  8. Chamkha A, Abbasbandy S, Rashad AM. Non-Darcy natural convection flow for non-Newtonian nanofluid over cone saturated in porous medium with uniform heat and volume fraction fluxes. Int J Numer Methods Heat Fluid Flow. 2015;25:422–37.

    Google Scholar 

  9. Laein RP, Rashidi S, Esfahani JA. Experimental investigation of nanofluid free convection over the vertical and horizontal flat plates with uniform heat flux by PIV. Adv Powder Technol. 2016;27:312–22.

    Google Scholar 

  10. Xun S, Zhao J, Zheng L, Zhang X. Bioconvection in rotating system immersed in nanofluid with temperature dependent viscosity and thermal conductivity. Int J Heat Mass Transf. 2017;111:1001–6.

    CAS  Google Scholar 

  11. Khan M, Azam M, Alshomrani AS. Unsteady slip flow of Carreau nanofluid over a wedge with nonlinear radiation and new mass flux condition. Results Phys. 2017;7:2261–70.

    Google Scholar 

  12. Mekheimer KS, Hasona WM, Abo-Elkhair RE, Zaher AZ. Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: application of cancer therapy. Phys Lett A. 2018;382:85–93.

    CAS  Google Scholar 

  13. Rashidi S, Akbarzadeh M, Karimi N, Masoodi R. Combined effects of nanofluid and transverse twisted-baffles on the flow structures, heat transfer and irreversibilities inside a square duct-a numerical study. Appl Therm Eng. 2018;130:135–48.

    CAS  Google Scholar 

  14. Zuhra S, Khan NS, Islam S. Magnetohydrodynamic second-grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comput Appl Math. 2018;37:6332–588.

    Google Scholar 

  15. Kumar PBS, Gireesha BJ, Mahanthesh B, Chamkha AJ. Thermal analysis of nanofluid flow containing gyrotactic microorganisms in bioconvection and second-order slip with convective condition. J Therm Anal Calorim. 2019;136:1947–57.

    Google Scholar 

  16. Alamri SZ, Ellahi R, Shehzad N, Zeeshan A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: an application of Stefan blowing. J Mol Liq. 2019;273:292–304.

    CAS  Google Scholar 

  17. Mahanthesh B, Lorenzini G, Oudina FM, Animasaun IL. Significance of exponential space-and thermal-dependent heat source effects on nanofluid flow due to radially elongated disk with Coriolis and Lorentz forces. J Therm Anal Calorim. 2019. https://doi.org/10.1007/s10973-019-08985-0.

    Article  Google Scholar 

  18. Waqas H, Khan SU, Imran M, Bhatti MM. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys Scr. 2019;94:115304.

    CAS  Google Scholar 

  19. Ellahi R, Hussain F, Abbas SA, Sarafraz MM, Goodarzi M, Shadloo MS. Study of two-phase Newtonian nanofluid flow hybrid with Hafnium particles under the effects of slip. Inventions. 2020;5:6.

    Google Scholar 

  20. Shahid A, Huang H, Bhatti MM, Zhang L, Ellahi R. Numerical investigation on the swimming of gyrotactic microorganisms in nanofluids through porous medium over a stretched surface. Mathematics. 2020;8:380.

    Google Scholar 

  21. Eid MR. Effects of NP shapes on non-Newtonian bio-nanofluid flow in suction/blowing process with convective condition: Sisko model. J Non-Equilibrium Thermodyn. 2020;45:97–108.

    CAS  Google Scholar 

  22. Hafeez A, Khan M, Ahmed J. Stagnation point flow of radiative Oldroyd-B nanofluid over a rotating disk. Comput Methods Prog Biomed. 2020;191:105342.

    Google Scholar 

  23. Lahmar S, Kezzar M, Eid MR, Sari MR. Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Phys A Stat Mech Appl. 2020;540:123138.

    Google Scholar 

  24. Turkyilmazoglu M. Single phase nanofluids in fluid mechanics and their hydrodynamic linear stability analysis. Comp Methods Prog Biomed. 2020;187:105171.

    Google Scholar 

  25. Ahmad M, Muhammad T, Ahmad I, Aly S. Time-dependent 3D flow of viscoelastic nanofluid over an unsteady stretching surface. Phys A Stat Mech Appl. 2020;551:124004.

    CAS  Google Scholar 

  26. Hassan A, Wahab A, Qasim MA, Janjua MM, Ali MA, Ali HM, Jadoon TR, Ali E, Raza A, Javaid N. Thermal management and uniform temperature regulation of photovoltaic modules using hybrid phase change materials-nanofluids system. Renew Energy. 2020;145:282–93.

    CAS  Google Scholar 

  27. Ba TL, Mahian O, Wongwises S, Szilágyi IM. Review on the recent progress in the preparation and stability of graphene-based nanofluids. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09365-9.

    Article  Google Scholar 

  28. Ullah N, Nadeem S, Khan AU. Finite element simulations for natural convective flow of nanofluid in a rectangular cavity having corrugated heated rods. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09378-4.

    Article  Google Scholar 

  29. Riaz A, Khan SUD, Zeeshan A, Khan SU, Hassan M, Muhammad T. Thermal analysis of peristaltic flow of nanosized particles within a curved channel with second-order partial slip and porous medium. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09454-9.

    Article  Google Scholar 

  30. Aziz T, Javaid S, Aziz A, Sadiq MA. Group theoretical analysis for magnetohydrodynamic generalized Stokes’ flow and radiative heat transfer model of a non-Newtonian nanofluid with heat generation/absorption. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09722-8.

    Article  Google Scholar 

  31. Darcy H. Les Fontaines Publiques De La Ville De Dijon. Paris: Victor Dalmont; 1856.

    Google Scholar 

  32. Forchheimer P. Wasserbewegung durch boden, Zeitschrift. Ver D Ing. 1901;45:1782–8.

    Google Scholar 

  33. Muskat M. The flow of homogeneous fluids through porous media. MI: Edwards; 1946.

    Google Scholar 

  34. Seddeek MA. Influence of viscous dissipation and thermophoresis on Darcy–Forchheimer mixed convection in a fluid saturated porous media. J Colloid Interface Sci. 2006;293:137–42.

    CAS  PubMed  Google Scholar 

  35. Pal D, Mondal H. Radiation effects on combined convection over a vertical flat plate embedded in a porous medium of variable porosity. Meccanica. 2009;44:133–44.

    Google Scholar 

  36. Pal D, Chatterjee S. Heat and mass transfer in MHD non-Darcian flow of a micropolar fluid over a stretching sheet embedded in a porous media with non-uniform heat source and thermal radiation. Commun Nonlinear Sci Numer Simul. 2010;15:843–57.

    Google Scholar 

  37. Singh AK, Kumar R, Singh U, Singh NP, Singh AK. Unsteady hydromagnetic convective flow in a vertical channel using Darcy–Brinkman–Forchheimer extended model with heat generation/absorption: analysis with asymmetric heating/cooling of the channel walls. Int J Heat Mass Transf. 2011;54:5633–42.

    Google Scholar 

  38. Gireesha BJ, Mahanthesh B, Manjunatha PT, Gorla RSR. Numerical solution for hydromagnetic boundary layer flow and heat transfer past a stretching surface embedded in non-Darcy porous medium with fluid-particle suspension. J Nig Math Soc. 2015;34:267–85.

    Google Scholar 

  39. Asma M, Othman WAM, Muhammad T. Numerical study for Darcy–Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics. 2019;7:921.

    Google Scholar 

  40. Majeed A, Zeeshan A, Noori FM. Analysis of chemically reactive species with mixed convection and Darcy–Forchheimer flow under activation energy: a novel application for geothermal reservoirs. J Therm Anal Calorim. 2020;140:2357–67.

    CAS  Google Scholar 

  41. Liao SJ. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun Nonlinear Sci Numer Simul. 2010;15:2003–16.

    Google Scholar 

  42. Dehghan M, Manafian J, Saadatmandi A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer Meth Partial Diff Eq. 2010;26:448–79.

    Google Scholar 

  43. Turkyilmazoglu M. An optimal analytic approximate solution for the limit cycle of duffing-van der pol equation. J Appl Mech. 2011;78:021005.

    Google Scholar 

  44. Malvandi A, Hedayati F, Domairry G. Stagnation point flow of a nanofluid toward an exponentially stretching sheet with nonuniform heat generation/absorption. J Thermodyn. 2013;2013:764827.

  45. Turkyilmazoglu M. An effective approach for evaluation of the optimal convergence control parameter in the homotopy analysis method. Filomat. 2016;30:1633–50.

    Google Scholar 

  46. Zhu J, Yang D, Zheng L, Zhang X. Effects of second order velocity slip and nanoparticles migration on flow of Buongiorno nanofluid. Appl Math Lett. 2016;52:183–91.

    Google Scholar 

  47. Haq RU, Hamouch Z, Hussain ST, Mekkaoui T. MHD mixed convection flow along a vertically heated sheet. Int J Hydrogen Energy. 2017;42:15925–32.

    Google Scholar 

  48. Farooq A, Ali R, Benim AC. Soret and Dufour effects on three dimensional Oldroyd-B fluid. Phys A Stat Mech Appl. 2018;503:345–54.

    Google Scholar 

  49. Gupta S, Kumar D, Singh J. MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation. Int J Heat Mass Transf. 2018;118:378–87.

    CAS  Google Scholar 

  50. Awais M, Awan SE, Iqbal K, Khan ZA, Raja MAZ. Hydromagnetic mixed convective flow over a wall with variable thickness and Cattaneo-Christov heat flux model: OHAM analysis. Results Phys. 2018;8:621–7.

    Google Scholar 

Download references

Acknowledgements

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant Number (D-400-130-1441). The authors, therefore, gratefully acknowledge DSR technical and financial support.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    Malik Zaka Ullah & Fouad Mallawi

  2. Department of Mathematics, College of Sciences, King Khalid University, Abha, 61413, Saudi Arabia

    Taseer Muhammad

Authors
  1. Malik Zaka Ullah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Taseer Muhammad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fouad Mallawi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Taseer Muhammad.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ullah, M.Z., Muhammad, T. & Mallawi, F. On model for Darcy–Forchheimer 3D nanofluid flow subject to heat flux boundary condition. J Therm Anal Calorim 143, 2411–2418 (2021). https://doi.org/10.1007/s10973-020-09892-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-020-09892-5

Keywords

Search

Navigation