Abstract
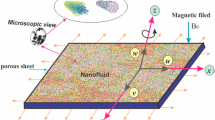
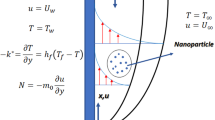
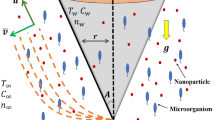
Cattaneo–Christov with variable thermal relaxation time and entropy generation is the main concern of this study. The micropolar fluid with absorption of heat in the existence of mixed convection and partial slip is scrutinized. Two distinct nanoparticles, i.e., single-wall carbon nanotube and multi-wall carbon nanotube, are immerged in micropolar fluid to interrogate the feature of heat and mass transfer. The non-dimensional similarity transformation is utilized to transform the partial differential equations into nonlinear ordinary differential equations, and resulting coupled equations are solved numerically using bvp4c from MATLAB. The present results show the fabulous agreement with previous published results. The temperature field diminishes with larger thermal relaxation time parameter. Entropy generation profile is an increasing function of Brinkmann number, while Bejan number is a diminishing function. Further the solid volume fraction diminishes the velocity profile and enhances the temperature distribution and entropy generation.


























Similar content being viewed by others
References
Farooq M, Ahmad S, Javed M, Anjum A. Chemically reactive species in squeezed flow through modified Fourier’s and Fick’s laws. Eur Phys J Plus. 2018;133:63.
Nadeem S, Ahmad S, Muhammad N. Cattaneo–Christov flux in the flow of a viscoelastic fluid in the presence of Newtonian heating. J Mol Liq. 2017;237:180–4.
Alamri SZ, Khan AA, Azeez M, Ellahi R. Effects of mass transfer on MHD second grade fluid towards stretching cylinder: a novel perspective of Cattaneo–Christov heat flux model. Phys Lett A. 2019;383(2–3):276–81.
Cattaneo C. Sulla conduzione del calore. Atti Sem Mat Fis Univ Modena. 1948;3:83–101.
Christov CI. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech Res Commun. 2009;36(4):481–6.
Shah Z, Tassaddiq A, Islam S, Alklaibi AM, Khan I. Cattaneo–Christov Heat Flux Model for Three-Dimensional Rotating Flow of SWCNT and MWCNT Nanofluid with Darcy-Forchheimer Porous Medium Induced by a Linearly Stretchable Surface. Symmetry. 2019;11(3):331.
Han S, Zheng L, Li C, Zhang X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Appl Math Lett. 2014;38:87–93.
Lu D, Ramzan M, Ahmad S, Chung JD, Farooq U. Upshot of binary chemical reaction and activation energy on carbon nanotubes with Cattaneo–Christov heat flux and buoyancy effects. Phys Fluids. 2017;29:123103.
Nadeem S, Ahmad S, Muhammad N, Mustafa MT. Chemically reactive species in the flow of a Maxwell fluid. Results Phys. 2017;7:2607–13.
Khan U, Ahmad S, Ramzan M, Suleman M, Lu D, Inam S. Numerical Simulation of Darcy-Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes. 2019;7(10):687.
Kumari M, Nath G. Unsteady incompressible boundary layer flow of a micropolar fluid at a stagnation point. Int J Eng Sci. 1984;22(6):755–68.
Eringen AC. Microcontinuum field theories: II. Fluent media, vol. 2. Berlin: Springer; 2001.
Lukaszewicz G. Micropolar fluids: theory and applications. Basel: Brikhauser; 1999.
Nadeem S, Khan MN, Muhammad N, Ahmad S. Erratum to: Mathematical analysis of bio-convective micropolar nanofluid Erratum to: Journal of Computational Design and Engineering. J Comput Des Eng. 2019;6:233–42.
Nadeem S, Rehman A, Vajravelu K, Lee J, Lee C. Axisymmetric stagnation flow of a micropolar nanofluid in a moving cylinder. Math Probl Eng. 2012. https://doi.org/10.1155/2012/378259.
Balaram M, Sastri VUK. Micropolar free convection flow. Int J Heat Mass Transf. 1973;16(2):437–41.
Das K. Slip effects on MHD mixed convection stagnation point flow of a micropolar fluid towards a shrinking vertical sheet. Comput Math Appl. 2012;63(1):255–67.
Maleki H, Safaei MR, Alrashed AAAA, Kasaeian A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J Therm Anal Calorim. 2019;135(3):1655–66.
Nazari S, Ellahi R, Sarafraz MM, Safaei MR, Asgari A, Akbari OA. Numerical study on mixed convection of a non-Newtonian nanofluid with porous media in a two lid-driven square cavity. J Therm Anal Calorim. 2019. https://doi.org/10.1007/s10973-019-08841-1.
Heydari A, Akbari OA, Safaei MR, Derakhshani M, Alrashed AAAA, Mashayekhi R, Shabani GAS, Zarringhalam M, Nguyen TK. The effect of attack angle of triangular ribs on heat transfer of nanofluids in a microchannel. J Therm Anal Calorim. 2018;131(3):2893–912.
Seth GS, Bhattacharyya A, Mishra MK. Study of partial slip mechanism on free convection flow of viscoelastic fluid past a nonlinearly stretching surface. Comput Therm Sci Int J. 2019;11(1–2):105–17.
Ellahi R, Hussain F, Ishtiaq F, Hussain A. Peristaltic transport of Jeffrey fluid in a rectangular duct through a porous medium under the effect of partial slip: An application to upgrade industrial sieves/filters. Pramana. 2019;93(3):34.
Zaib A, Haq RU, Chamkha AJ, Rashidi MM. Impact of partial slip on mixed convective flow towards a Riga plate comprising micropolar TiO2-kerosene/water nanoparticles. Int J Numer Methods Heat Fluid Flow. 2019;29(5):1647–62.
Ariel PD. Axisymmetric flow due to a stretching sheet with partial slip. Comput Math Appl. 2007;54(7–8):1169–83.
Bejan A. A study of entropy generation in fundamental convective heat transfer. J Heat Transf. 1979;101(4):718–25.
Bejan A, Kestin J. Entropy generation through heat and fluid flow. J Appl Mech. 1983;50:475.
Bhatti MM, Sheikholeslami M, Shahid A, Hassan M, Abbas T. Entropy generation on the interaction of nanoparticles over a stretched surface with thermal radiation. Colloids Surf A. 2019;570:368–76.
Ellahi R, Sait SM, Shehzad N, Mobin N. Numerical simulation and mathematical modeling of electro-osmotic Couette-Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry. 2019;11(8):1038.
Alkanhal TA, Sheikholeslami M, Arabkoohsar A, Haq R, Shafee A, Li Z, Tlili I. Simulation of convection heat transfer of magnetic nanoparticles including entropy generation using CVFEM. Int J Heat Mass Transf. 2019;136:146–56.
Choi SUS, Zhang ZG, Yu W, Lockwood FE, Grulke EA. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett. 2001;79(14):2252–4.
Ahmed Z, Nadeem S, Saleem S, Ellahi R. Numerical study of unsteady flow and heat transfer CNT-based MHD nanofluid with variable viscosity over a permeable shrinking surface. Int J Numer Methods Heat Fluid Flow. 2019;29(12):4607–23.
Akbar NS, Khan ZH, Nadeem S. The combined effects of slip and convective boundary conditions on stagnation-point flow of CNT suspended nanofluid over a stretching sheet. J Mol Liq. 2014;196:21–5.
Haq RU, Nadeem S, Khan ZH, Noor NFM. Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Phys B. 2015;457:40–7.
Nasir S, Islam S, Gul T, Shah Z, Khan MA, Khan W, Khan AZ, Khan S. Three-dimensional rotating flow of MHD single wall carbon nanotubes over a stretching sheet in presence of thermal radiation. Appl Nanosci. 2018;8(6):1361–78.
Saba F, Ahmed N, Hussain S, Khan U, Mohyud-Din S, Darus M. Thermal analysis of nanofluid flow over a curved stretching surface suspended by carbon nanotubes with internal heat generation. Appl Sci. 2018;8(3):395.
Hayat T, Farooq M, Alsaedi A. Homogeneous-heterogeneous reactions in the stagnation point flow of carbon nanotubes with Newtonian heating. AIP Adv. 2015;5(2):027130.
Zeeshan A, Ellahi R, Mabood F, Hussain F. Numerical study on bi-phase coupled stress fluid in the presence of Hafnium and metallic nanoparticles over an inclined plane. Int J Numer Methods Heat Fluid Flow. 2019;29(8):2854–69.
Jain S, Gupta P. Flow and heat transfer of carbon nanotubes nanofluid flow over a 3-D inclined nonlinear stretching sheet with porous media. In: Srinivasacharya D., Reddy K, editors. Numerical heat transfer and fluid flow. Lecture notes in mechanical engineering. Singapore: Springer; 2019. p. 321–9.
Nadeem S, Ahmad S, Muhammad N. Computational study of Falkner-Skan problem for a static and moving wedge. Sens Actuators B Chem. 2018;263:69–76.
Prakash J, Tripathi D, Tiwari AK, Sait SM, Ellahi R. “Peristaltic pumping of nanofluids through a tapered channel in a porous environment: Applications in blood flow. Symmetry. 2019;11(7):868.
Suleman M, Ramzan M, Ahmad S, Lu D. Numerical simulation for homogeneous–heterogeneous reactions and Newtonian heating in the silver-water nanofluid flow past a nonlinear stretched cylinder. Phys Scr. 2019;94(8):085702.
Sarafraz MM, Pourmehran O, Yang B, Arjomandi M, Ellahi R. Pool boiling heat transfer characteristics of iron oxide nano-suspension under constant magnetic field. Int J Therm Sci. 2020;147:106131.
Khan LA, Raza M, Mir NA, Ellahi R. Effects of different shapes of nanoparticles on peristaltic flow of MHD nanofluids filled in an asymmetric channel. J Therm Anal Calorim. 2019. https://doi.org/10.1007/s10973-019-08348-9.
Nasiri H, Jamalabadi MYA, Sadeghi R, Safaei MR, Nguyen TK, Shadloo MS. A smoothed particle hydrodynamics approach for numerical simulation of nano-fluid flows. J Therm Anal Calorim. 2019;135(3):1733–41.
Zaib A, Haq RU. Magnetohydrodynamics mixed convective flow driven through a static wedge including TiO2 nanomaterial with micropolar liquid: Similarity dual solutions via finite difference method. Proc Inst Mech Eng C J Mech Eng Sci. 2019;233:5813–25.
Yih KA. MHD forced convection flow adjacent to a non-isothermal wedge. Int Commun Heat Mass Transf. 1999;26(6):819–27.
White FM. Fluid mechanics. McGraw Hill; 2015.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ahmad, S., Nadeem, S., Muhammad, N. et al. Cattaneo–Christov heat flux model for stagnation point flow of micropolar nanofluid toward a nonlinear stretching surface with slip effects. J Therm Anal Calorim 143, 1187–1199 (2021). https://doi.org/10.1007/s10973-020-09504-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10973-020-09504-2