Skip to main content
SpringerLink
Log in

The shapes of critical loci of binary fluid mixtures on the p–T plane

The relations of those shapes with the positions of the critical points of their component fluids

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

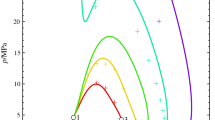
The relations between the shapes of the critical loci of binary fluid mixtures and the positions of the critical points of their component fluids on the p–T plane were considered theoretically. The consideration was carried out for vapor–liquid phase equilibria in the model systems without liquid–liquid equilibria. We focused only the relations between the shapes and the tangent of the straight lines connecting the critical points of the component fluids on the p–T plane, and so the effects of the distance between the critical points were out of the scope of this work. The changes in the shapes of the critical loci were classified logically into three patterns. Literature survey has shown that the two patterns exist in the experimental results for several types of mixtures. The shapes of the critical loci of the binary fluid mixtures on the p–T plane are closely related to the relative positions between the critical points of their component fluids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Hicks CP, Young CL. The gas–liquid critical properties of binary mixtures. Chem Rev. 1975;75:119–75.

    Article  CAS  Google Scholar 

  2. Dohrn R, Brunner G. High-pressure fluid-phase equilibria: experimental methods and systems investigated (1988–1993). Fluid Phase Equilib. 1995;106:213–82.

    Article  CAS  Google Scholar 

  3. Polishuk I, Wisniak J, Segura H. Simultaneous prediction of the critical and sub-critical phase behavior in mixtures using equation of state I. Carbon dioxide–alkanols. Chem Eng Sci. 2001;56:6485–510.

    Article  CAS  Google Scholar 

  4. Polishuk I, Wisniak J, Segura H. Simultaneous prediction of the critical and sub-critical phase behavior in mixtures using equations of state II. Carbon dioxide–heavy n-alkanes. Chem Eng Sci. 2003;58:2529–50.

    Article  CAS  Google Scholar 

  5. Polishuk I, Wisniak J, Segura H. Simultaneous prediction of the critical and sub-critical phase behavior in mixtures using equations of state III. Methane–n-alkanes. Chem Eng Sci. 2003;58:4363–76.

    Article  CAS  Google Scholar 

  6. Van Konynenburg PH, Scott RL. Critical lines and phase equilibria in binary van der Waals mixtures. Phil Trans R Soc Lond A. 1980;298:495–540.

    Article  Google Scholar 

  7. Rowlinson JS, Swinton FL. Liquids and liquid mixtures. 3rd ed. London: Butterworths Scientific; 1982. p. 191–4.

    Google Scholar 

  8. Kay WB. The critical locus curve and the phase behavior of mixtures. Acc Chem Res. 1968;1:344–51.

    Article  CAS  Google Scholar 

  9. Kay WB. P–T–x diagrams in the critical region. Acetone–n-alkane systems. J Phys Chem. 1964;68:827–31.

    Article  CAS  Google Scholar 

  10. Poettmann FH, Katz DL. Phase behavior of binary carbon dioxide: paraffin systems. Ind Eng Chem. 1945;37:847–53.

    Article  CAS  Google Scholar 

  11. Ohgaki K, Katayama T. Isothermal vapor–liquid equilibrium data for the ethane–carbon dioxide system at high pressures. Fluid Phase Equilib. 1977;1:27–32.

    Article  Google Scholar 

  12. Kay WB, Albert RE. Liquid–vapor equilibrium relations in the ethane–cyclohexane system. Ind Eng Chem. 1956;48:422–6.

    Article  CAS  Google Scholar 

  13. Pak SC, Kay WB. The critical properties of binary hydrocarbon systems. Ind Eng Chem Fundam. 1972;11:255–67.

    Article  CAS  Google Scholar 

  14. Sage BH, Lacey WN, Schaafsma JG. Phase equilibria in hydrocarbon systems II. Methane–propane system. Ind Eng Chem. 1934;26:214–7.

    Article  CAS  Google Scholar 

  15. Akers WW, Burns JF, Fairchild WR. Low-temperature phase equilibria. Methane–propane system. Ind Eng Chem. 1954;46:2531–4.

    Article  CAS  Google Scholar 

  16. Wichterle I, Kobayashi R. Vapor–liquid equilibrium of methane–propane system at low temperatures and high pressures. J Chem Eng Data. 1972;17:4–9.

    Article  CAS  Google Scholar 

  17. McCurdy JL, Katz DL. Phase equilibria in the system. Ethane–ethylene–acetylene. Ind Eng Chem. 1944;36:674–80.

    Article  CAS  Google Scholar 

  18. Diefenbacher A, Türk M. Critical (p, ρ, T) properties of CH2F2, {xCO2 + (1 − x)SF6}, {xSF6 + (1 − x)CH2F2}, and {xCHF3 + (1 − x)CH2F2}. J Chem Thermodyn. 1999;31:905–19.

    Article  CAS  Google Scholar 

Download references

Acknowledgments

This work was partly supported by the fund for Agriomics project from the Ministry of Education, Culture, Sports, Science and Technology, Japan.

Author information

Authors and Affiliations

  1. Faculty of Agriculture, Meijo University, Shiogamaguchi 1-501, Tenpaku-ku, Nagoya, 468-8502, Japan

    Koki Tsukamoto, Guosong Fang, Masahiro Maebayashi & Masaharu Ohba

Authors
  1. Koki Tsukamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guosong Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Masahiro Maebayashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Masaharu Ohba
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Koki Tsukamoto.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tsukamoto, K., Fang, G., Maebayashi, M. et al. The shapes of critical loci of binary fluid mixtures on the p–T plane. J Therm Anal Calorim 113, 1551–1554 (2013). https://doi.org/10.1007/s10973-013-3073-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-013-3073-8

Keywords

Search

Navigation