Abstract
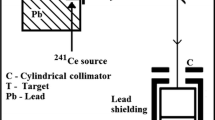
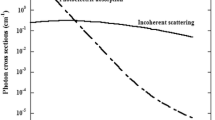
In this paper, multiple scattering of 662 keV gamma photons from targets of Carbon, Aluminium, Iron, Copper and polymers (Polypropylene, Polycarbonate, Polymethyl methacrylate, Polytetraflouroethylene and Polyvinyl chloride) is studied experimentally. Backscattered photons are detected by a NaI(Tl) detector placed at an angle of 90° to the incident beam. The single scattered events are reconstructed analytically to extract multiple scattered photons from the measured spectra. We observe that the number of backscattered photons increases with an increase in target thickness, and saturates at a particular value of the target thickness. This saturation thickness decreases with increasing atomic number of the target. The saturation thickness of the multiple scattering is used to assign effective atomic number of polymers. The experimental results are compared with the results obtained by Monte Carlo N-particle simulation code.









Similar content being viewed by others
References
Icelli O (2006) Practical method for experimental effective atomic number in the coherent to Compton scattering ratio. J Quant Spectrosc Radiat Transf 101:151–158
Gowda S, Krishnaveni S, Yashoda T, Umesh TK, Ramakrishna Gowda (2004) Photon mass attenuation coefficients, effective atomic numbers and electron densities of some thermoluminescent dosimetric compounds. Pramana 63:529–541
Manjunathaguru V, Umesh TK (2006) Effective atomic numbers and electron densities of some biologically important compounds containing H, C, N and O in the energy range 145–1330 keV. J Phys B At Mol Opt Phys 39:3969–3981
Singh M, Singh B, Sandhu BS (2009) Investigations of multiple scattering of 320 keV γ rays: a new technique for assigning effective atomic number to composite material. Phys Scr 79:035101
Singh G, Singh M, Sandhu BS, Singh B (2008) Experimental investigations of multiple scattering of 662 keV gamma photons in elements and binary alloys. Appl Radiat Isot 66:1151–1159
Sabharwal AD, Singh B, Sandhu BS (2009), Investigations of multiple backscattering and albedos of 1.12 MeV gamma photons in elements and alloys. Nucl Instrum Methods Phys Res B 267:151–156
Singh M, Singh G, Singh B, Sandhu BS (2008) Experimental observation of energy dependence of saturation thickness of multiply scattered gamma photons. Radiat Phys Chem 77:991–995
Akar Tarim U, Ozmutlu EN, Gurler O, Yalcin S (2013) Monte Carlo analysis of multiple backscattering of gamma rays. J Radioanal Nucl Chem 295:901–905
Singh M, Singh G, Sandhu BS, Singh B (2006) Effect of detector collimator and sample thickness on 0.662 MeV multiply Compton-scattered gamma rays. Appl Radiat Isot 64:373–378
Paramesh L, Venkataramaiah P, Gopala K Sanjeeviah H (1983) Z-dependence of saturation depth for multiple backscattering of 662 keV photons from thick samples. Nucl Instrum Methods 206:327–330
Pitkanen T, Laundy D Holt RS, Cooper MJ (1986) The multiple scattering profile in gamma ray Compton studies. Nucl Instrum Methods Phys Res A 251:536–544
Tanner AC, Epstein IR (1976) Multiple scattering in the Compton effect. I. Analytic treatment of angular distributions and total scattering probabilities. Phys Rev A 13:335–348
Halonen V, Williams B (1979) Multiple scattering in the compton effect, relativistic cross section for double scattering. Phys Rev B 19:1990–1998
Felsteiner J, Pattison P, Cooper MJ (1974) Effect of multiple scattering on experimental Compton profiles: a Montel Carlo calculation. Philos Maj 30:537–548
Nghiep TD, Khai NT, Cong NT, Minh DTN (2013) Characterization of a material by probability of linear scattering using effect of target thickness. J Radioanal Nucl Chem 295:1039–1042
Crouthamel CE (1970) Applied gamma ray spectroscopy, 2nd edn, Pergamon Press, New York
Ravindraswami K, Kiran KU, Eshwarappa KM, Somashekarappa HM (2013), Experimental observations of Z-dependence of saturation thicknesses of 662 keV gamma rays in metals and glasses. Indian J Phys 87:1141–1147
Knoll GF (1988) Radiation detection and measurements, 3rd edn. Wiley, New York
Taylor ML, Smith RL, Dossing F, Franich RD (2012) Robust calculation of effective atomic numbers: the auto-Z eff software. Med Phys 39:1769–1778
Faiz M Khan (2003) The Physics of radiation therapy, 3rd edn. Lippincott Williams & Wilkins, Philadelphia.
Briesmeister JF (1993) MCNP a general purpose Monte Carlo N-particle transport code, Version 4A, Los Alamos National Laboratory report LA-12625
Kucuk N, Cakir M, Isitman NA (2013) Mass attenuation coefficients, effective atomic numbers and effective electron densities for some polymers. Radiat Prot Dosim 153(1):127134
Naydenov SV, Ryzhikov VD, Smith CF (2004) Direct reconstruction of the effective atomic number of materials by the method of multi-energy radiography. Nucl Instrum Methods Phys Res B 215:552560
Kumar SP, Manjunathaguru V, Umesh TK (2010) Effective atomic numbers of some H-, C-, N- and O-based composite materials derived from differential incoherent scattering cross-sections. PRAMANA J Phys 74(4):555–562
Acknowledgments
Authors are grateful to University Grants Commission, Government of India for providing financial assistance in the form of Major Research Project. Kiran K U would like to thank University Grants Commission for providing FIP teacher fellowship. The experiment was carried out in Center for Application of Radioisotopes and Radiation Technology (CARRT), Mangalore University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ravindraswami, K., Kiran, K.U., Eshwarappa, K.M. et al. Non destructive evaluation of selected polymers by multiple scattering of 662 keV gamma rays. J Radioanal Nucl Chem 300, 997–1003 (2014). https://doi.org/10.1007/s10967-014-3075-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10967-014-3075-4