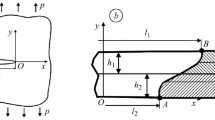
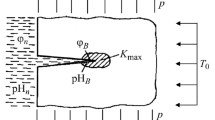
We formulate computational models used to determine the durability of plates with systems of cracks under the action of long-term static loads, high temperatures, and hydrogen-containing environments. These models are based on the first law of thermodynamics, i.e., on the balance of energy components and rates of their changes in metallic materials containing macrocracks and subjected to long-term tension, high-temperature field, and hydrogen-containing environments. We also consider specific cases of periodic and doubly periodic systems of cracks.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O. E. Andreikiv and O. V. Hembara, Fracture Mechanics and Durability of Metallic Materials in Hydrogen-Containing Media [in Ukrainian], Naukova Dumka, Kyiv (2008).
O. E. Andreikiv, M. B. Kit, and S. V. Khyl’, “Evaluation of the residual life of a cracked plate under block loading,” Fiz.-Khim. Mekh. Mater., 47, No. 4, 62–70 (2011); English translation: Mater. Sci., 47, No. 4, 488–498 (2012).
O. E. Andreikiv, R. M. Lesiv, and I. Ya. Dolins’ka, “Dependence of the period of subcritical growth of a creep fatigue crack on the duration of loading cycles,” Fiz.-Khim. Mekh. Mater., 45, No. 4, 31–38 (2009); English translation: Mater. Sci., 45, No. 4, 494–503 (2009).
O. E. Andreikiv and N. B. Sas, “A mathematical model for determining the period of the subcritical propagation of cracks of hightemperature creep in solids,” Dopov. NAN Ukr., No. 5, 47–52 (2006).
O. E. Andreikiv and N. B. Sas, “Fracture mechanics of metallic plates under conditions of high-temperature creep,” Fiz.-Khim. Mekh. Mater, 42, No. 2, 62–68 (2006); English translation: Mater. Sci., 42, No. 2, 210–219 (2006).
O. Andreikiv, L. Dobrovol’s’ka, I. Dolins’ka, and N. Yavors’ka, “Effect of hydrogen on the growth of creep-fatigue cracks in thinwalled structural elements,” Visnyk Ternopil’. Nats. Tekh. Univ., No. 4 (72), 7–15 (2013).
L. Babii, O. Student, and A. Zahors’kyi, “Properties of 15Kh2MFA hull steel under the conditions of creep in gaseous hydrogen,” Fiz.-Khim. Mekh. Mater., Special issue No. 7, Vol. 1, 100–105 (2008).
A. M. Lokoshchenko, “Creep and long-term strength of metals in corrosive media (Review),” Fiz.-Khim. Mekh. Mater., 37, No. 4, 27–41 (2001); English translation: Mater. Sci., 37, No. 4, 559–572 (2001).
G. P. Mel’nikov, Durability of Structural Elements under the Conditions of High Temperatures in Benchmark Tests [in Russian], Atomizdat, Moscow (1979).
V. I. Nikitin, Physicochemical Phenomena in the Interaction between Liquid and Solid Metals [in Russian], Atomizdat, Moscow (1967).
V. L. Danilov and S. V. Zarubin, “Steel creep and creep rupture strength in environment containing hydrogen,” in: R. K. Penny (editor), Proc. Fourth Internat. Colloq. “Aging of Materials and Methods for the Assessment of Lifetimes of Engineering Plant” (Cape Town, South Africa, Apr. 21–25, 1997), Balkema, Rotterdam (1997), pp. 113–116.
F. Garofalo, Fundamentals of Creep and Creep-Rupture in Metals, MacMillan, New York (1970).
Yu. Murakami (editor), Stress Intensity Factors. Handbook, Pergamon, Oxford (1987).
M. Yatomi, K. M. Nikbin, and N. P. O’Dowd, “Creep crack growth prediction using a damage based approach,” Int. J. Pres. Ves. Pip., 80, No. 7–8, 573–583 (2003).
Author information
Authors and Affiliations
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 57, No. 1, pp. 97–104, January–April, 2014.
Rights and permissions
About this article
Cite this article
Andreikiv, O.E., Yavors’ka, N.V. & Kukhar, V.Z. Mathematical Models for Estimating the Residual Life of Plates with Systems of Cracks Under the Action of Long-Term Static Loads, High Temperatures, and Hydrogen. J Math Sci 212, 121–130 (2016). https://doi.org/10.1007/s10958-015-2653-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-015-2653-5