Skip to main content
SpringerLink
Log in

Axisymmetric Problem for an Elastic Cylinder of Finite Length with Fixed Lateral Surface with Regard for its Weight

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

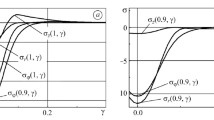
We consider an elastic cylinder with regard for its weight. The conditions of sliding fixing are imposed on the lower base of the cylinder, its upper base is subjected to the action of an axisymmetric normal load, and the lateral surface is fixed. The Hankel integral transform is used to reduce the problem to an integral equation of the first kind for normal stresses acting on the fixed cylindrical surface. After finding the singularities of the unknown function, the solution of the integral equation is sought in the form of a series in Jacobi polynomials. The results of numerical evaluation of the normal stresses on the fixed surface of the cylinder are obtained both with regard for its weight and by neglecting its weight.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. B. L. Abramyan and A. Ya. Aleksandrov, “Axisymmetric problem of the theory of elasticity,” in: Proc. of the Second All-Union Congr. on Theoretical and Applied Mechanics [in Russian], Issue 3, Nauka, Moscow (1966), pp. 7–37.

  2. H. Bateman and A. Erdélyi, Higher Transcendental Functions, Vol. 2: Bessel Functions, Parabolic Cylinder Functions, and Orthogonal Polynomials, McGraw-Hill, New York (1953).

  3. G. N. Bukharinov, “On the problem of equilibrium of elastic circular cylinder,” Vestn. Leningrad. Univ. Ser. Mat., Phiz., Khim., No. 2, 23–33 (1952).

  4. G. M. Valov, “On the axisymmetric deformation of a continuous circular cylinder of finite length,” Prikl. Mat. Mekh., 26, No. 4, 650–667 (1962).

    MathSciNet  Google Scholar 

  5. V. M. Vihak and Yu. V. Tokovyy, “Exact solution of an axisymmetric problem of the theory of elasticity in stresses for a continuous cylinder of certain length,” Prykl. Probl. Mekh. Mat., Issue 1, 55–60 (2003).

  6. O. O. Kapshivyi, “On the application of р-analytic functions in the axisymmetric problem of the theory of elasticity,” Visn. Kyiv. Univ. Ser. Mat. Mekh., Issue 1, No. 5, 76–89 (1962).

  7. M. A. Koltunov, Yu. N. Vasil’ev, and V. A. Chernykh, Elasticity and Strength of Cylindrical Bodies [in Russian], Vysshaya Shkola, Moscow (1975).

  8. W. Nowacki, Thermoelasticity, Pergamon, London (1962).

    Google Scholar 

  9. V. Z. Parton and P. I. Perlin, Methods of the Mathematical Theory of Elasticity [in Russian], Nauka, Moscow (1981).

    Google Scholar 

  10. G. Ya. Popov, “New transforms for the resolving equations in elastic theory and new integral transforms, with applications to boundary-value problems of mechanics,” Prikl. Mekh., 39, No. 12, 46–73 (2003); English translation: Int. Appl. Mech., 39, No. 12, 1400–1424 (2003).

  11. G. Ya. Popov, “Axisymmetric boundary-value problems of the theory of elasticity for cylinders and cones of finite length,” Dokl. Ross. Akad. Nauk, 439, No. 2, 192–197 (2011).

    Google Scholar 

  12. A. P. Prudnikov, Yu. A. Brychkov, and O. I. Marichev, Integrals and Series. Elementary Functions [in Russian], Nauka, Moscow (1981).

  13. I. N. Sneddon, Fourier Transforms, McGraw-Hill, New York (1951).

    Google Scholar 

  14. Yu. V. Tokovyy, “Axisymmetric stresses in a finite elastic cylinder under the action of normal pressure uniformly distributed over a part of the lateral surface,” Prykl. Probl. Mekh. Mat., Issue 8, 144–151 (2010).

  15. Ya. S. Uflyand, Integral Transforms in Problems of the Theory of Elasticity [in Russian], Nauka, Leningrad (1968).

  16. E. Jahnke, F. Emde, and F. Lösch, Tafeln Höherer Funktionen, Teubner, Stuttgart (1960).

    MATH  Google Scholar 

  17. K. T. Chau and X. X. Wei, “Finite solid circular cylinders subjected to arbitrary surface load. Part I. Analytic solution,” Int. J. Solids Struct., 37, No. 40, 5707–5732 (2000).

    Article  MATH  Google Scholar 

  18. K. T. Chau and X. X. Wei, “Finite solid circular cylinders subjected to arbitrary surface load. Part II. Application to double-punch test,” Int. J. Solids Struct., 37, No. 40, 5733–5744 (2000).

    Article  Google Scholar 

  19. K. T. Chau and X. X. Wei, “A new analytic solution for the diametral point load strength test on finite solid circular cylinders,” Int. J. Solids Struct., 38, No. 9, 1459–1481 (2001).

    Article  MATH  Google Scholar 

  20. S. D. Conte, K. L. Miller, and C. B. Sensenig, “The numerical solution of axisymmetric problems in elasticity,” in: D. P. Legalley (editor), Ballistic Missile and Space Technology. Proc. of the Fifth Symp. on Ballistic Missile and Space Technology, Vol. 4, Academic Press, New York–London (1960), pp. 173–202.

Download references

Author information

Authors and Affiliations

  1. Mechnikov Odessa National University, Odessa, Ukraine

    G. Ya. Popov & Yu. S. Protserov

Authors
  1. G. Ya. Popov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu. S. Protserov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 57, No. 1, pp. 57–68, January–March, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Popov, G.Y., Protserov, Y.S. Axisymmetric Problem for an Elastic Cylinder of Finite Length with Fixed Lateral Surface with Regard for its Weight. J Math Sci 212, 67–82 (2016). https://doi.org/10.1007/s10958-015-2649-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-015-2649-1

Keywords

Search

Navigation