Skip to main content
SpringerLink
Log in

Qualitative Methods for the Investigation of a Mathematical Model of Nonlinear Vibrations of a Conveyer Belt

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

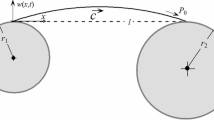
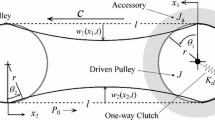
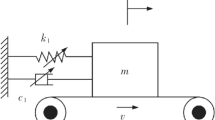
We describe a procedure used for the qualitative investigation of the solution of a mathematical model of vibrations of a conveyer belt based on the general approaches of the theory of nonlinear boundary-value problems. We consider the behavior of a vibrating system at a time fairly distant from the initial moment. The proposed procedure is based on the application of the method of monotonicity and Galerkin’s method and enables us to prove the correctness of the solution of the problem and use various approximate methods for its investigation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. O. Kolin’ko, S. P. Lavrenyuk, and P. Ya. Pukach, “Fourier problem for a nonlinear second-order hyperbolic equation,” Visn. L’viv. Univ. Ser. Mekh.-Mat., Issue 62, 67–79 (2003).

  2. S. P. Lavrenyuk and P. Ya. Pukach, “Mixed problem for a nonlinear hyperbolic equation in a domain unbounded with respect to space variables,” Ukr. Mat. Zh., 59, No. 11, 1523–1531 (2007); English translation : Ukr. Math. J., 59, No. 11, 1708–1718 (2007).

    Article  MathSciNet  Google Scholar 

  3. Ya. G. Panovko, Introduction to the Theory of Mechanical Vibrations [in Russian], Nauka, Moscow (1991).

    Google Scholar 

  4. P. Ya. Pukach, “Mixed problem in an infinite domain for a weakly nonlinear hyperbolic equation with increasing coefficients,” Mat. Met. Fiz.-Mekh. Polya, 47, No. 4, 149–154 (2004).

    MATH  MathSciNet  Google Scholar 

  5. B. I. Sokil, “Investigation of nonlinear vibrations of conveyer belts,” Optym. Vyrobn. Prots. Tekhnol. Kontr. Mashynobud. Pryladobud., No. 394, 101–104 (2000).

  6. A. V. Metrikine, “Steady state response of an infinite string on a nonlinear viscoelastic foundation to moving point loads,” J. Sound Vibr., 272, 1033–1046 (2004).

    Article  Google Scholar 

  7. D. M. Santee and P. B. Goncalves, “Oscillations of a beam on a nonlinear elastic foundation under periodic loads,” Shock Vibr., 13, 273–284 (2006).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics and Fundamental Sciences, “L’vivs’ka Politekhnika” National University, Lviv, Ukraine

    P. Ya. Pukach

Authors
  1. P. Ya. Pukach
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 55, No. 4, pp. 30–35, October–December, 2012.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pukach, P.Y. Qualitative Methods for the Investigation of a Mathematical Model of Nonlinear Vibrations of a Conveyer Belt. J Math Sci 198, 31–38 (2014). https://doi.org/10.1007/s10958-014-1770-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-014-1770-x

Keywords

Search

Navigation