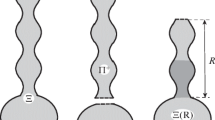
General elliptic boundary value problems with spectral parameter are studied in a domain \( G \subset {\mathbb{R}^{n + 1}} \) with several “quasicylindrical exits” at infinity. The problems are selfadjoint relative to the Green formula. The coefficients of the boundary value problems are smooth and are slowly stabilized at each exit at infinity to functions that are periodic with respect to the axis t-coordinate. We describe the asymptotics of solutions at infinity. We formulate a well-posed problem with radiation conditions, introduce a unitary scattering matrix, and justify a method for computing this matrix. The results are new even in the particular case where the role of “quasicylinders” are played by usual cylinders (with a constant cross-section) and the coefficients are stabilized at infinity to functions independent of the axis coordinate. Bibliography: 12 titles.
Similar content being viewed by others
References
S. A. Nazarov and B. A. Plamenevskii, Elliptic Problems in Domains with Piecewise Smooth Boundary [in Russian], Nauka, Moscow (1991).
B. A. Plamenevskii and O. V. Sarafanov, “On a method for computing the scattering matrices for waveguides” [in Russian], Algebra Anal. 23, No. 1, 200-231 (2011).
B. A. Plamenevskii and O. V. Sarafanov, “On a method for computing waveguide scattering matrices in the presence of point spectrum,” arxiv.org/abs/1106.5975.
I. C. Gohberg and M. G. Krein, “Fundamental aspects of defect numbers, root numbers, and indexes of linear operators” [in Russian], Uspekhi Mat. Nauk 12, No. 2, 43–119 (1957).
I. C. Gohberg and E. I. Sigal, “An operator generalization of the logarithmic residue theorem and the theorem of Rouché” [in Russian], Mat. Sb. 84, 607–629 (1971); English transl.: Math. USSR Sb. 13, 603–625, 1971.
V. G. Maz’ya and B. A. Plamenevskii, “Estimates in L p and in Hölder classes and the Miranda–Agmon principle for solutions of elliptic boundary value problems in domains with singular points at the boundary” [in Russian], Math. Nachr. 81, 25–82 (1978); English transl.: In : Elliptic Boundary Value Problems, Am. Math. Soc. Transl. (2) 123, 1-57 (1984).
B. A. Plamenevskii, “On spectral properties of elliptic problems in domains with cylindrical ends,” Am. Math. Soc. Transl. (2) 220, 123–139 (2007).
V. Grikurov and E. Heikkola, P. Neittaanmäki, B. Plamenevskii, “On computation of scattering matrices and on surface waves for diffraction gratings,” Numer. Math. 94, No. 2, 269–288 (2003).
J. L. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems and Applications, Springer, Berlin etc (1972).
P. Grisvard, Elliptic Problems in Nonsmooth Domains, Pitman, Boston (1985).
V. A. Kozlov, V. G. Maz’ya, and J. Rossmann, Elliptic Boundary Value Problems in Domains with Point Singularities, Am. Math. Soc., Providence, RI (1997).
F. John, M. Schechter, and L. Bers, Partial Differential Equations, Am. Math. Soc., Providence, RI (1992).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Problems in Mathematical Analysis 64, 2012, p. 93–117.
Rights and permissions
About this article
Cite this article
Neittaanmäki, P., Plamenevskii, B.A. & Sarafanov, O.V. Radiation and scattering in domains with periodic waveguides under slow stabilization of characteristics of a medium. J Math Sci 184, 331–361 (2012). https://doi.org/10.1007/s10958-012-0871-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-012-0871-7