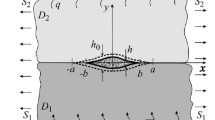
We have formulated the problem of thermoelasticity for a bimaterial whose components differ only in their shear moduli, with a closed interfacial crack having rough surfaces. The bimaterial is subjected to the action of compressive loads and heat flow normal to the interfacial surface. We have taken into account the dependence of thermal conductance of the defect on the contact pressure of its faces and heat conductivity of the medium that fills it. The problem is reduced to a Prandtl-type nonlinear singular integro-differential equation for temperature jump between the crack surfaces. An analytical solution of this problem has been constructed for the case of action of the heat flow only. We have analyzed the dependence of contact pressure of the defect faces, temperature jump between them, and the intensity factor of tangential interfacial stresses on the value of given heat flow, roughness of the surfaces, and ratio between the shear moduli of joined materials.
Similar content being viewed by others
References
A. O. Andreikiv, “Generalized Griffith problem of shear with regard for the roughness of the crack surfaces,” Fiz.-Khim. Mekh. Mater., 36, No. 2, 49–54 (2000); English translation: Mater. Sci., 36, No. 2, 210–217 (2000).
G. S. Kit and M. G. Krivtsun, Plane Problems of Thermoelasticity for Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1983).
G. S. Kit, S. P. Nagalka, and R. M. Martynyak, “Nonlinear contact problem of thermoelasticity for a crack at the interface between materials with different thermal properties,” in: Theoretical and Applied Mechanics [in Russian], Issue 33 (2001), pp. 13–21.
H. S. Kit and R. M. Martynyak, “Thermoelasticity of a piecewise homogeneous body with a closed interfacial crack in the presence of contact thermal resistance between its faces,” Dopov. Nats. Akad. Nauk Ukr., No. 10, 84–88 (1996).
H. S. Kit, R. M. Martynyak, and S. P. Nahalka, “Thermoelastic effects in a body with a crack closed by concentrated forces,” Mat. Metody Fiz.-Mekh. Polya, 42, No. 2, 101–107 (1999).
R. M. Martynyak, Mechanical-Thermal-and-Diffusion Interaction of Bodies with Contact-Surface Inhomogeneities and Defects [in Ukrainian], Doctoral Degree Thesis (Phys., Math.), Lviv (2000).
R. M. Martynyak, “Thermal opening of an initially closed interface crack under conditions of imperfect thermal contact between its faces,” Fiz.-Khim. Mekh. Mater., 35, No. 5, 14–22 (1999); English translation: Mater. Sci., 35, No. 5, 612–622 (1999).
R. M. Martynyak, Kh. I. Honchar, and S. P. Nahalka, “Simulation of thermomechanical closure of an initially open interface crack with heat resistance,” Fiz.-Khim. Mekh. Mater., 39, No. 5, 59–66 (2003); English translation: Mater. Sci., 39, No. 5, 672–681 (2003).
R. M. Martynyak and Kh. I. Gonchar, “Thermoelastic deformation of a bimaterial with an interfacial defect filled with a heatconducting medium,” in: Theoretical and Applied Mechanics [in Russian], Issue 41 (2005), pp. 58–62.
Yu. N. Shlykov, E. A. Ganin, and S. N. Tsarevskii, Contact Thermal Resistance [in Russian], Énergiya, Moscow (1977).
J. R. Barber and M. Comninou, “The penny-shaped interface crack with heat flow. Part 2: Imperfect contact,” Trans. ASME, J. Appl. Mech., 50, No. 4a, 770–776 (1983).
A. M. Garsia and H. Sehitoglu, “Contact of crack surfaces during fatigue: Part 1. Formulation of the model,” Metallurgical Mater. Trans., A, 28A, No. 11, 2263–2275 (1997).
G. I. Giannopoulos and N. K. Anifantis, “A BEM analysis for thermomechanical closure of interfacial cracks incorporating friction and thermal resistance,” Comput. Meth. Appl. Mech. Eng., 196, No. 4–6, 1018–1029 (2007).
T. S. Gross and D. A. Mendelsohn, “On the effect of crack face contact and friction due to fracture surface roughness in edge crack subjected to external shear,” Eng. Fract. Mech., 31, No. 3, 405–420 (1988).
L. K. Keppas and N. K. Anifantis, “Boundary element prediction on TBC fracture resistance,” Fatigue Fract. Eng. Mater. Struct., 33, No. 3, 174–182 (2010).
I. V. Kharun and V. V. Loboda, “A thermoelastic problem for interface crack with contact zones,” Int. J. Solids Struct., 41, No. 1, 159–175 (2004).
T. Kobayashi and D. A. Shockey, “Fracture surface topography analysis (FRASTA) – Development, accomplishments and future applications,” Eng. Fract. Mech., 77, No. 12, 2370–2384 (2010).
D. A. Mendelsohn, T. S. Gross, R. U. Goulet, and M. Zhouc, “Experimental-computational estimation of rough fracture surface contact stresses,” Mater. Sci. Eng., A, 249, No. 1–2, 1–6 (1998).
J. A. Newman and R. S. Piascik, “Interactions of plasticity and oxide crack closure mechanisms near the fatigue crack growth threshold,” Int. J. Fatigue, 26, No. 9, 923–927 (2004).
F. O. Riemelmoser and R. Pippan, “Crack closure: a concept of fatigue crack growth under examination,” Fatigue Fract. Eng. Mater. Struct., 20, No. 11, 1529–1540 (1997).
H. Sehitoglu and A. M. Garsia, “Contact of crack surfaces during fatigue: Part 2. Simulations,” Metallurgical Mater. Trans., A, 28A, No. 11, 2277–2289 (1997).
C. O. A. Semprimoschnig, J. Stampfl, R. Pippan, and O. Kolednik, “A new powerful tool for surveying cleavage fracture surface,” Fatigue Fract. Eng. Mater. Struct., 20, No. 11, 1541–1550 (1997).
Author information
Authors and Affiliations
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 53, No. 1, pp. 71–79, January–March, 2010.
Rights and permissions
About this article
Cite this article
Martynyak, R.M. Thermal stress state of a bimaterial with a closed interfacial crack having rough surfaces. J Math Sci 176, 578–589 (2011). https://doi.org/10.1007/s10958-011-0423-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-011-0423-6