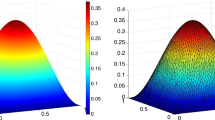
A variational problem of determination of the amplitude of the velocity vector of elastic displacements and the electric potential of a piezoelectric with instantaneous memory that executes steady-state vibrations under the influence of harmonic loads of given circular frequency is formulated. We establish conditions of well-posedness of this class of problems and find a priori estimates of convergence of approximations of the finite-element method to their solution. A posteriori error estimators of approximations of the finite-element method, which enable us to determine the distribution of energy norms of errors by solving local problems of the residual of approximation at each finite element of triangulation, are constructed. An algorithm for calculating estimators of this type is described in detail for two-dimensional problems for both triangular and tetragonal finite elements, which may be extended to the three-dimensional case. The efficiency and reliability of the estimator of piecewise bilinear approximations of the finite-element method is illustrated by numerical solutions of a model problem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O. Yu. Zharii and A. F. Ulitko, Introduction to Mechanics of Nonstationary Vibrations and Waves [in Russian], Vyshcha Shkola, Kiev (1989).
H. Kvasnytsya and H. A. Shynkarenko, “Comparison of simple a posteriori estimators of errors of the finite-element method for problems of elastostatics,” Visn. L’viv. Univ. Ser. Prykl. Mat. Inform., Issue 7, 162–174 (2003).
W. Nowacki, Efekty Elektromagnetyczne w Stalych Cialach Odksztalcalnych, PWN, Warsaw (1993).
V. Z. Parton and B. A. Kudryavtsev, Electromagnetoelasticity of Piezoelectric and Electroconducting Bodies [in Russian], Nauka, Moscow (1988).
H. A. Shynkarenko, “Statement and solvability of initial boundary-value problems of electroviscoelasticity,” Visn. L’viv. Univ. Ser. Mekh.-Mat., Issue 33, 10–16 (1990).
G. A. Shinkarenko, “Projection-mesh approximations for variational problems of pyroelectricity. I. Statement of problems and analysis of steady-state forced vibrations,” Differ. Uravn., 29, No. 7, 1252–1260 (1993).
N. A. Shul’ga and A. M. Bolkisev, Vibrations of Piezoelectric Bodies [in Russian], Naukova Dumka, Kiev (1990).
F. V. Chaban and H. A. Shynkarenko, “Constructing of h-adaptive finite-element method for piezoelectricity problem,” Zh. Obchysl. Prykl. Mat. Ser. Obchysl. Mat., 97, Issue 1 (97), 1–9 (2009).
F. Chaban and H. Shynkarenko, “The construction and analysis of a posteriori error estimators for piezoelectricity stationary problems,” Oper. Theory: Adv. Appl., 191, 291–304 (2009).
A. Premount, Mechatronics: Dynamics of Electromechanical and Piezoelectric Systems, Springer, Berlin (2006).
J. Yang, An Introduction to the Theory of Piezoelectricity, Springer, Berlin (2005).
Author information
Authors and Affiliations
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 52, No. 4, pp. 88–98, October–December, 2009.
Rights and permissions
About this article
Cite this article
Chaban, F.V., Shynkarenko, H.A. A posteriori error estimators of finite-element approximations for problems of forced harmonic vibrations of piezoelectrics. J Math Sci 174, 229–242 (2011). https://doi.org/10.1007/s10958-011-0293-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-011-0293-y