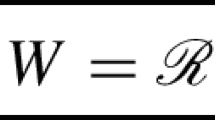Skip to main content

Advertisement

SpringerLink
Log in

Generalizations of Korn’s inequality based on gradient estimates in Orlicz spaces and applications to variational problems in 2D involving the trace free part of the symmetric gradient

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

We prove variants of Korn’s inequality involving the deviatoric part of the symmetric gradient of fields \( u:{\mathbb{R}^2} \supset \Omega \to {\mathbb{R}^2} \) belonging to Orlicz–Sobolev classes. These inequalities are derived with the help of gradient estimates for the Poisson equation in Orlicz spaces. We apply these Korn type inequalities to variational integrals of the form

$$ \int\limits_\Omega {h\left( {\left| {{\varepsilon^D}(u)} \right|} \right)dx} $$

occurring in General Relativity and prove C 1,α–regularity results for minimizers under rather general conditions on the N–function h. A further useful tool for this analysis is an appropriate version of the (Sobolev-) Poincaré inequality with εD(u) measuring the distance of u to the holomorphic functions. Bibliography: 20 titles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Zeidler, Nonlinear Functional Analysis and Its Applications, vol. IV, Springer, Berlin etc. (1987).

  2. S. Dain, “Generalized Korn’s inequality and conformal Killing vectors,” Calc. Var. 25, No. 4, 535–540 (2006).

    Article  MATH  MathSciNet  Google Scholar 

  3. R. A. Adams, Sobolev Spaces, Academic Press, New York etc. (1975).

    MATH  Google Scholar 

  4. R. Bartnik, J. Isenberg, “The constraint equation,” In: P. T. Chruściel, E. Friedrich, H. (Eds.), The Einstein Equations and Large Scale Behaviour of Gravitational Fields, pp. 1–38. Birkhäuser, Basel etc. (2004).

  5. O. Schirra, PhD Thesis (2009).

  6. M. Fuchs, O. Schirra, “An application of a new coercive inequality to variational problems studied in general relativity and in Cosserat elasticity giving the smoothness of minimizers,” Archiv Math. [To appear]

  7. M. M. Rao, Z. D. Ren, Theory of Orlicz Spaces, Marcel Dekker, New York etc. (1991).

    MATH  Google Scholar 

  8. H. Jia, D. Li, L. Wang, “Regularity theory in Orlicz spaces for elliptic equations in Reifenberg domains,” J. Math. Anal. Appl. 334, 804–817 (2007).

    Article  MATH  MathSciNet  Google Scholar 

  9. F. Yao, Y. Sun, S. Zhou, “Gradient estimates in Orlicz spaces for quasilinear elliptic equation,” Nonlinear Anal. 69, 2553–2565 (2008).

    Article  MATH  MathSciNet  Google Scholar 

  10. S.-S. Byun, F. Yao, S. Zhou, “Gradient estimates in Orlicz space for nonlinear elliptic equations,” J. Funct. Anal. 255, 1851–1873 (2008).

    MATH  MathSciNet  Google Scholar 

  11. M. Fuchs, “A note on non–uniformly elliptic Stokes–type systems in two variables,” J. Mat. Fluid Mech. (DOI 10.1007/s 00021-008-0285y)

  12. M. Bildhauer, M. Fuchs, X. Zhong, “A lemma on the higher integrability of functions with applications to the regularity theory of two dimensional generalized Newtonian fluids,” Manus. Math. 116, No. 2, 135–156 (2005).

    Article  MATH  MathSciNet  Google Scholar 

  13. N. G. Meyers, “An L p–estimate for the gradient of solutions of second order elliptic divergence equation,” Ann. S.N.S Pisa III, No. 17, 189–206 (1963).

  14. M. Bildhauer, M. Fuchs, “Differentiability and higher integrability results for local minimizers of splitting type variational integrals in 2D with applications to nonlinear Hencky–materials” Calc. Var. (DOI 10.1007/s 00526-009-0257-y).

  15. M. Giaquinta, Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems, Princeton Univ. Press, Princeton (1983).

    MATH  Google Scholar 

  16. D. Gilbarg, N. S. Trudinger, Elliptic Partial Differential Equations of Second Order, Springer, Berlin etc. (1998).

    Google Scholar 

  17. J. Kauhanen, P. Koskela, J. Mal´y, “On functions with derivatives in a Lorentz space,” Manus. Math. 100, 87–101 (1999).

    Article  MATH  MathSciNet  Google Scholar 

  18. L. Hörmander, An Introduction to Complex Analysis in Several Variables, North–Holland (1973).

  19. F. Sauvigny, Partielle Differentialgleichungen der Geometrie und der Physik. Band 1 Grundlagen und Integraldarstellungen, Springer, Berlin etc. (2003).

  20. E. M. Stein, Singular Integrals and Differentiability Properties of Functions, Princeton University Press, Princeton (1970).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Universität des Saarlandes, Fachbereich 6.1 Mathematik Postfach 15 11 50, D–66041, Saarbrücken, Germany

    M. Fuchs

Authors
  1. M. Fuchs
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Fuchs.

Additional information

Translated from Problems in Mathematical Analysis 46, April 2010, pp. 125–139.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fuchs, M. Generalizations of Korn’s inequality based on gradient estimates in Orlicz spaces and applications to variational problems in 2D involving the trace free part of the symmetric gradient. J Math Sci 167, 418–434 (2010). https://doi.org/10.1007/s10958-010-9927-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-010-9927-8

Keywords

Search

Navigation