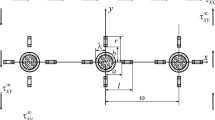
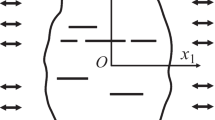
In the present work, a model of nonlinear deformation of stochastic composites under microdamaging is developed for the case of a composite with orthotropic inclusions, when microdefects are accumulated in the matrix. The composite is treated as an isotropic matrix strengthened by triaxial arbitrarily oriented ellipsoidal inclusions with orthotropic symmetry of the elastic properties. It is assumed that the process of loading leads to accumulation of damage in the matrix. Fractured microvolumes are modeled by a system of randomly distributed quasispherical pores. The porosity balance equation and relations for determining the effective elastic modules in the case of orthotropic components are taken as basic relations. The fracture criterion is specified as the limiting value of the intensity of average shear stresses acting in the intact part of the material. On the basis of the analytic and numerical approach, we propose an algorithm for the determination of nonlinear deformation properties of the investigated material. The nonlinearity of composite deformations is caused by the finiteness of deformations. By using the numerical solution, the nonlinear stress–strain diagrams are predicted and discussed for an orthotropic composite material for various cases of orientation of inclusions in the matrix.
Similar content being viewed by others
References
S. D. Akbarov, “On the stress state in a fibrous composite material with twisted fibers,” in: Mathematical Methods and Physicomechanical Fields, Issue 31, 74–79 (1990).
V. L. Bogdanov, “Axisymmetric problem of a subsurface mode I crack in a composite material with residual stresses,” Mat. Met. Fiz.-Mekh. Polya, 50, No. 2, 45–54 (2007).
L. M. Kachanov, Foundations of Fracture Mechanics [in Russian], Nauka, Moscow (1974).
V. I. Lavrenyuk and V. M. Tereshchenko, “Stress state of piecewise-homogeneous bodies under the action of nonstationary thermal fields,” Mat. Met. Fiz.-Mekh. Polya, 40, No. 1, 53–58 (1997).
L. V. Nazarenko, “Effect of microdefects on the deformation properties of anisotropic materials,” Dopov. Nats. Akad. Nauk Ukr., No. 10, 63–67 (1999).
A. R. Rzhanitsyn, Theory of Reliability of Structures [in Russian], Stroiizdat, Moscow (1978).
I. N. Frantsevich, F. F. Voronov, and S. A. Bakuta, Elastic Constants and Elastic Moduli of Metals and Nonmetals [in Russian], Naukova Dumka, Kiev (1982).
L. P. Khoroshun, B. P. Maslov, E. N. Shikula, and L. V. Nazarenko, Statistical Mechanics and Effective Properties of Materials [in Russian], Naukova Dumka, Kiev (1993).
L. P. Khoroshun, “Methods of the theory of random functions in determining the macroscopic properties of microheterogeneous media,” Int. Appl. Mech., 14, No. 2, 3–17 (1978).
L. P. Khoroshun, “Principles of the micromechanics of material damage. 1. Short-term damage,” Int. Appl. Mech., 34, No. 10, 120–127 (1998).
L. P. Khoroshun and L. V. Nazarenko, “Deformation and microdamaging of discretely-fibrous composites with transverselyisotropic components,” Int. Appl. Mech., 39, No. 6, 696–703 (2003).
L. P. Khoroshun and L. V. Nazarenko, “Model of short-term damaging of transversely isotropic materials,” Int. Appl. Mech., 37, No. 1, 74–83 (2001).
L. P. Khoroshun and L. V. Nazarenko, “Thermoelasticity of orthotropic composites with ellipsoidal inclusions,” Int. Appl. Mech., 26, No. 9, 805–812 (1990).
L. P. Khoroshun and E. N. Shikula, “Deformation of composite material under microdestructions,” Int. Appl. Mech., 32, No. 6, 52–58 (1996).
L. P. Khoroshun and E. N. Shikula, “Effect of the spread of strength characteristics on the deformation of granular composite under microdestructions,” Int. Appl. Mech., 33, No. 8, 39–45 (1997).
L. P. Khoroshun and E. N. Shikula, “Short-term microdestructions of fibrous materials with transversely isotropic fibers under temperature influences,” Int. Appl. Mech., 38, No. 6, 74–83 (2002).
L. P. Khoroshun and E. N. Shikula, “To the theory of short-term microdestructions of composite materials of granular structure under temperature influences,” Int. Appl. Mech., 38, No. 1, 79–87 (2002).
L. V. Nazarenko, “Deformation of orthotropic composites with unidirectional ellipsoidal inclusions under the conditions of matrix microdamage,” Mat. Met. Fiz.-Mekh. Polya, 51, No. 1, 121–130 (2008).
L. V. Nazarenko, “Elastic properties of materials with ellipsoidal pores,” Int. Appl. Mech., 32, No. 1, 46–53 (1996).
Author information
Authors and Affiliations
Additional information
Published in Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 51, No. 4, pp. 181–192, October–December, 2008.
Rights and permissions
About this article
Cite this article
Nazarenko, L.V. Deformation of composites with arbitrarily oriented orthotropic fibers under matrix microdamages. J Math Sci 167, 217–231 (2010). https://doi.org/10.1007/s10958-010-9916-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-010-9916-y