Skip to main content
SpringerLink
Log in

Some problems of mathematical modeling in thermomechanics of bodies of various transparencies subjected to thermal irradiation

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

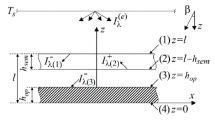
Features of the statement of problems of thermomechanics for solids of various transparencies for thermal radiation are presented. Approximate approaches to the calculation of temperature in semitransparent solids are analyzed. We investigate the influence of the effects of radiation and transfer of thermal energy on temperatures and stresses in semitransparent and opaque solids on a model problem for an irradiated layer.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. N. Andrianov, Fundamentals of Radiation and Complex Heat Exchange [in Russian], Énergiya, Moscow (1972).

    Google Scholar 

  2. Yu. N. Barabanenkov, “Multiple wave scattering on an ensemble of particles and the theory of radiation transfer,” Usp. Fiz. Nauk, 117, No. 1, 46–78 (1975).

    Google Scholar 

  3. Yu. N. Barabanenkov and B. M. Finkel’berg, “Method of Green functions in the theory of multiple wave scattering,” in: Theoretical and Applied Problems of Light Scattering [in Russian], Nauka i Tekhnika, Minsk (1974), pp. 171–187.

    Google Scholar 

  4. A. G. Blokh, Ya. A. Zhuravlev, and L. N. Ryzhkov, Heat Exchange by Radiation. A Handbook [in Russian], Énergoatomizdat, Moscow (1991).

    Google Scholar 

  5. M. Brukhal’, R. Terletskii, and O. Fundak, “Technique for the numerical solution of nonlinear problems of heat transfer in bodies of different transparence for heat radiation,” Visn. Lviv. Univ. Ser. Prykl. Mat. Inform., Issue 13, 59–71 (2007).

  6. Ya. Yo. Burak, A. R. Gachkevich, and R. F. Terletskii, “Thermomechanics of bodies of low electric conductivity in external quasistationary electromagnetic fields,” Dokl. Akad. Nauk USSR. Ser. A, No. 7, 38–41 (1989).

  7. Ya. Yo. Burak, O. R. Hachkevych, and R. F. Terlets’kyi, “Thermomechanics of multicomponent bodies of low electric conductivity,” in: Modeling and Optimization in Thermomechanics of Electroconductive Inhomogeneous Bodies [in Ukrainian], Vol. 1, SPOLOM, Lviv (2006).

  8. Ya. I. Burak, O. R. Hachkevych, and R. F. Terlets’kyi, “Thermomechanics of bodies of low electric conductivity under the action of electromagnetic radiation of the infrared frequency range,” Dopov. Akad. Nauk Ukr. RSR, Ser. A, No. 6, 39–43 (1990).

  9. A. A. Burka, N. A. Rubtsov, P. I. Stepanenko, and A. D. Khripunov, “Investigation of nonstationary radiation–conductive heat exchange in selectively absorbing media,” in: Heat–Mass Exchange, Vol. 7: Heat Exchange by Radiation and Complex Heat Exchange [in Russian], Part 2, Izd. Akad. Nauk Bel. SSR, Minsk (1980), pp. 103–112.

  10. A. A. Burka, N. A. Rubtsov, and V. P. Stupin, “Theoretical and experimental investigation of heating regimes of organic glass,” in: Heat–Mass Exchange [in Russian], Vol. 6, Part 2, Izd. Akad. Nauk Bel. SSR, Minsk (1980), pp. 132–138.

  11. A. R. Gachkevich, “Determination and optimization of the thermally stressed state of electrically conducting bodies in external quasistationary electromagnetic fields,” J. Math. Sci., 67, No. 2, 2930–2934 (1993).

    Article  Google Scholar 

  12. A. R. Gachkevich, Thermomechanics of Electroconductive Bodies under the Action of Quasistationary Electromagnetic Fields [in Russian], Naukova Dumka, Kiev (1992).

    Google Scholar 

  13. A. R. Gachkevich, Thermoelasticity of Electroconductive Bodies under the Action of Electromagnetic Radiation of Infrared Frequency Range [in Russian], Preprint No. 10-93, Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, Lvov(1993).

  14. A. R. Gachkevich and V. Ya. Boichuk, “Thermomechanical behavior of nonmetallic electrical conductors during high-temperature treatment,” J. Math. Sci., 86, No. 2, 2585–2589 (1997).

    Article  Google Scholar 

  15. A. R. Gachkevich, V. O. Drabyk, B. S. Malkiel', and R. F. Terletskii, “The thermally stressed state of the glass shell of a kinescope under heating by electromagnetic radiation,” J. Math. Sci., 65, No. 5, 1837–1840 (1993).

    Article  Google Scholar 

  16. O. R. Hachkevych, “Mathematical models of thermomechanics of magnetizable and polarizable electrically conducting bodies subject to quasisteady electromagnetic radiation,” J. Math. Sci., 97, No. 1, 3846–3853 (1999).

    Article  Google Scholar 

  17. O. R. Hachkevych, M. H. Hachkevych, Yu. R. Sosnovyi, and R. F. Terlets’kyi, “Modeling of heating regimes of electrovacuum instruments using electromagnetic radiation,” Avtomat. Vyrob. Prots. Mashynobud. Pryladobud., Issue 33, 51–61 (1998).

    Google Scholar 

  18. O. R. Hachkevych and O. B. Humenchuk, “Thermoelastic state of a glass hollow sphere under the action of external electromagnetic radiation,” Visn. Derzh. Univ. “Lviv. Politekhn.” Ser. Prykl. Matem., No. 341, 82–92 (1998).

  19. O. R. Hachkevych and R. F. Terletskyi, “Models of thermomechanics of magnetizable and polarizable conducting deformable solids,” Mater. Sci., 40, No. 3, 320–336 (2004).

    Google Scholar 

  20. O. R. Hachkevych, R. F. Terlets’kyi, and T. L. Kurnyts’kyi, “Mechanothermodiffusion in semitransparent bodies,” in: Modeling and Optimization in Thermomechanics of Electroconductive Inhomogeneous Bodies [in Ukrainian], Vol. 2, SPOLOM, Lviv (2007).

    Google Scholar 

  21. B. A. Grigor’ev, Pulse Heating by Radiation [in Russian], Vol. 1, Nauka, Moscow (1974).

    Google Scholar 

  22. B. A. Grigor’ev, Pulse Heating by Radiation [in Russian], Vol. 2, Nauka, Moscow (1974).

    Google Scholar 

  23. N. B. Delone, Interaction of Laser Radiation with a Matter [in Russian], Nauka, Moscow (1989).

    Google Scholar 

  24. Y. Jaluria, Natural Convection: Heat and Mass Exchange, Pergamon Press, Oxford (1980).

    Google Scholar 

  25. V. N. Eliseev, “Nonstationary temperature field of a semitransparent shell with inhomogeneously distributed heat sources,” Izv. Vysch. Uchebn. Zaved., Ser. Mashinostroenie, No. 12, 52–59 (1971).

  26. V. N. Eliseev, “Generalized solution of a three-dimensional problem of nonstationary heat conduction with volume absorption of radiant energy,” Trudy MVTU, No. 205, 5–43 (1976).

    Google Scholar 

  27. R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, McGraw Hill, New York (1971).

    Google Scholar 

  28. A. E. Sheidlin (editor), Radiating Properties of Solid Materials. A Handbook [in Russian], Energiya, Moscow (1974).

    Google Scholar 

  29. A. D. Kovalenko, Fundamentals of Thermoelasticity [in Russian], Naukova Dumka, Kiev (1970).

    Google Scholar 

  30. Yu. M. Kolyano and I. I. Bernar, “Temperature-induced stresses in a plate under bilateral laser treatment,” Probl. Prochn., No. 5, 36–48 (1983).

    Google Scholar 

  31. Yu. M. Kolyano and A. N. Kulik, Temperature Stresses Induced by Volume Sources [in Russian], Naukova Dumka, Kiev (1983).

    Google Scholar 

  32. F. Kreith and W. Z. Black, Basic Heat Transfer, Harper & Row, New York (1980).

    Google Scholar 

  33. L. N. Lavrikov and Yu. F. Yurchenko, Thermal Properties of Metals and Alloys [in Russian], Naukova Dumka, Kiev (1985).

    Google Scholar 

  34. L. D. Landau and E. M. Lifshits, Field Theory [in Russian], Nauka, Moscow (1973).

    Google Scholar 

  35. L. D. Landau and E. M. Lifshits, Electrodynamics of Continuous Media [in Russian], Nauka, Moscow (1959).

    Google Scholar 

  36. M. L. Levin and E. M. Ryzhov, Theory of Equilibrium Heat Fluctuations in Electrodynamics [in Russian], Nauka, Moscow (1967).

    Google Scholar 

  37. A. V. Lykov, Theory of Heat Conduction [in Russian], Vysshaya Shkola, Moscow (1967).

    Google Scholar 

  38. B. S. Malkiel’, A. R. Gachkevich, Yu. R. Sosnovyi and R. F. Terletskii, “Temperature fields and stresses in a system of planeparallel layers under heating by electromagnetic radiation,” J. Math. Sci., 63, No. 1, 23–27 (1993).

    Article  Google Scholar 

  39. M. D. Mashkovich, Electric Properties of Inorganic Dielectrics in the Ultrahigh Frequency Range [in Russian], Sovetskoe Radio, Moscow (1969).

    Google Scholar 

  40. W. Nowacki, Dynamic Problems in Thermoelasticity, Noordhoff International Publishing, Leyden (1975).

    Google Scholar 

  41. V. A. Petrov and N. V. Marchenko, Energy Transfer in Partially Transparent Solid Materials [in Russian], Nauka, Moscow (1985).

    Google Scholar 

  42. G. V. Plyatsko and Ya. S. Pidstryhach, “On the stressed state induced by a laser beam in the process of fracture of transparent polymers,” Fiz.-Khim. Mekh. Mater., 6, No. 3, 93–97 (1970).

    Google Scholar 

  43. Ya. S. Pidstryhach and Yu. M. Kolyano, Generalized Thermomechanics [in Russian], Naukova Dumka, Kiev (1976).

    Google Scholar 

  44. V. S. Popovych, G. Yu. Harmatii, and O. M. Vovk, “Thermoelastic state of a thermosensitive space with a spherical cavity under conditions of convective-radiation heat exchange,” Mat. Met. Fiz.-Mekh. Polya, 49, No. 3, 168–176 (2006).

    MATH  Google Scholar 

  45. Yu. S. Postol’nyk and A. P. Ohurtsov, Nonlinear Applied Thermomechanics [in Russian], NMTs VO MONU, Kiev (2000).

    Google Scholar 

  46. V. I. Baranovskii (editor), Production of Color Picture Tubes [in Russian], Energiya, Moscow (1978).

    Google Scholar 

  47. B. Rous, Glass in Electronics [in Russian], Sovetskoe Radio, Moscow (1969).

    Google Scholar 

  48. N. A. Rubtsov, Heat Exchange by Radiation in Continuous Media [in Russian], Nauka, Novosibirsk (1984).

    Google Scholar 

  49. N. A. Rubtsov and S. D. Sleptsov, “Influence of boundary conditions on nonstationary radiative–conductive heat exchange in a layer of semitransparent medium,” Teplofiz. Aérodinam., 12, No. 1, 95–103 (2005).

    Google Scholar 

  50. N. N. Rykalin, A. A. Uglov, and L. M. Anishchenko, High Temperature Technological Processes. Thermophysical Fundamentals [in Russian], Nauka, Moscow (1985).

    Google Scholar 

  51. N. N. Rykalin, A. A. Uglov, and A. N. Kokora, Laser Treatment [in Russian], Mashinostroenie, Moscow (1975).

    Google Scholar 

  52. S. B. Maslenkov and E. A. Maslenkova, Steels and Alloys for High Temperatures. A Handbook [in Russian], Part 1, Metallurgiya, Moscow (1991).

    Google Scholar 

  53. R. F. Terletskii, Thermostressed State of Bodies of Low Electric Conductivity under the Action of Electromagnetic Radiation [in Russian], Author’s Thesis of the Candidate Degree Thesis (Physicomathematical Sciences), Lvov (1988).

  54. C. L. Tien, “Radiation properties of gases,” in Advances in Heat Transfer [Russian translation], Mir, Moscow (1971), pp. 280–360.

    Google Scholar 

  55. A. A. Uglov, Yu. M. Kolyano, A. N. Kulik, and F. I. Stotskii, “Stresses in plane bodies with absorption under the action of a local heat source,” Fiz. Khim. Obrab. Mater., No. 6, 117–120 (1976).

    Google Scholar 

  56. C. A. Wert and R. M. Thomson, Physics of Solids, McGraw-Hill, New York (1970).

    Google Scholar 

  57. W. Espe, Materials of High Vacuum Technology, Vol. 2, Pergamon Press, Oxford (1968).

    Google Scholar 

  58. R. E. Field and R. Viskanta, “Measurement and prediction of dynamic temperatures in unsymmetrically cooled glass windows,” J. Thermophys. Heat Transfer, 7, 616–623 (1993).

    Article  Google Scholar 

  59. J. D. Fowler, “Radiation-induced RF loss measurements and thermal stresses calculation for ceramic windows,” J. Nuclear Matter., 123, 1359 (1984).

    Article  Google Scholar 

  60. T. Heping, B. Maestre, and M. Lallemand, “Transient and steady-state combined heat transfer in semitransparent materials subjected of a pulse or a step irradiation,” Heat Transfer, 133, 166–173 (1991).

    Article  Google Scholar 

  61. R. B. Hetnarski and F. C. de Bolt, “Thermal stresses due to laser radiation. Part 1: heat conduction,” J. Therm. Stresses, 15, 331–333 (1990).

    Article  Google Scholar 

  62. R. B. Hetnarski, L. G. Hector, P. Hosseini Tehrani, and M. R. Eslami, “Thermal stresses due to a laser pulse train: Coupled solution,” in: Thermal Stresses’99. Proc. of the 3rd Int. Congress on Thermal Stresses, (Cracow, June 13–17, 1999), Cracow University of Technology, Cracow (1999), pp. 61–64.

  63. K. Hutter and A. A. van de Ven, “Field-matter interaction in thermoelastic solids,” in: Lecture Notes in Physics, Vol. 88, Berlin: Springer, (1978).

  64. Ju. A. Krawcow and Ju. I. Or_ow, Optyka Geometryczna O_rodków Niejednorodnych, Wydawnictwo Naukowo-Techniczne, Warszawa (1993).

  65. N. A. Rubtsov and E. B. Timmerman, “Thermoelasic processes in semitransparent material under the condition of interaction between thermal and strain fields,” Numer. Heat Transfer., 21, 249–260 (1992).

    Article  Google Scholar 

  66. R. Siegel, “Transient effects of radiative transfer in semitransparent materials,” Int. J. Eng. Sci,. 36, 1701–1739 (1998).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, Ukrainian National Academy of Sciences, Lviv, Ukraine

    A. R. Hachkevych, R. F. Terletskii & M. B. Brukhal’

  2. Technical University of Opole, Opole, Poland

    A. R. Hachkevych

Authors
  1. A. R. Hachkevych
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. F. Terletskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. B. Brukhal’
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 51, No. 3, pp. 202–219, July–September, 2008.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hachkevych, A.R., Terletskii, R.F. & Brukhal’, M.B. Some problems of mathematical modeling in thermomechanics of bodies of various transparencies subjected to thermal irradiation. J Math Sci 165, 403–425 (2010). https://doi.org/10.1007/s10958-010-9808-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-010-9808-1

Keywords

Search

Navigation